Solving the laplace equation

第十三次

---

The summary:

We have encountered many partial differential equation in our learning process, and we knew many analytical ways to solve it. There are three impotant partial differential equations, that is laplace equation (equilibrium state), diffusion equation，and wave equation. If we apply variables separation to the diffusion and wave equation, we will get Helmholtz equation，that can be ragarded as a kind of laplace equation. So we solve the laplace equation in this chapter. A numerical way is applied to the equation and solve two problems in electrodynamics. The most important procedure is certainly the finite difference of the equation.

The psudocode:

Just like the diffence of time in the ordinary differential equation, we did the finite difference of time and space position. Actually, the partical equations are derived through finite differential ways. Here, we use the two-dimentional finite differential form as follows:

$$V_{new}(i,j)=\frac{1}{4}[V_{old}(i+1,j)+V_{old}(i-1,j)+V_{old}(i,j-1)+V_{old}(i,j+1)]$$
This is called Jacobo mathod, I will use this mathod to salve the capacitor problem and the point charge problem. In the process of writting the codes, the judgement of the condition $\Delta V< \Delta V_S$ is actually an AND condition, how to judge it is important. In the program, I make a 100x100 array to store the potential value of the syatem, that is really too big and the calculation consume a lot of time.

The result:

• First, the capacitor problem have been solved just like the textbook told us:
  
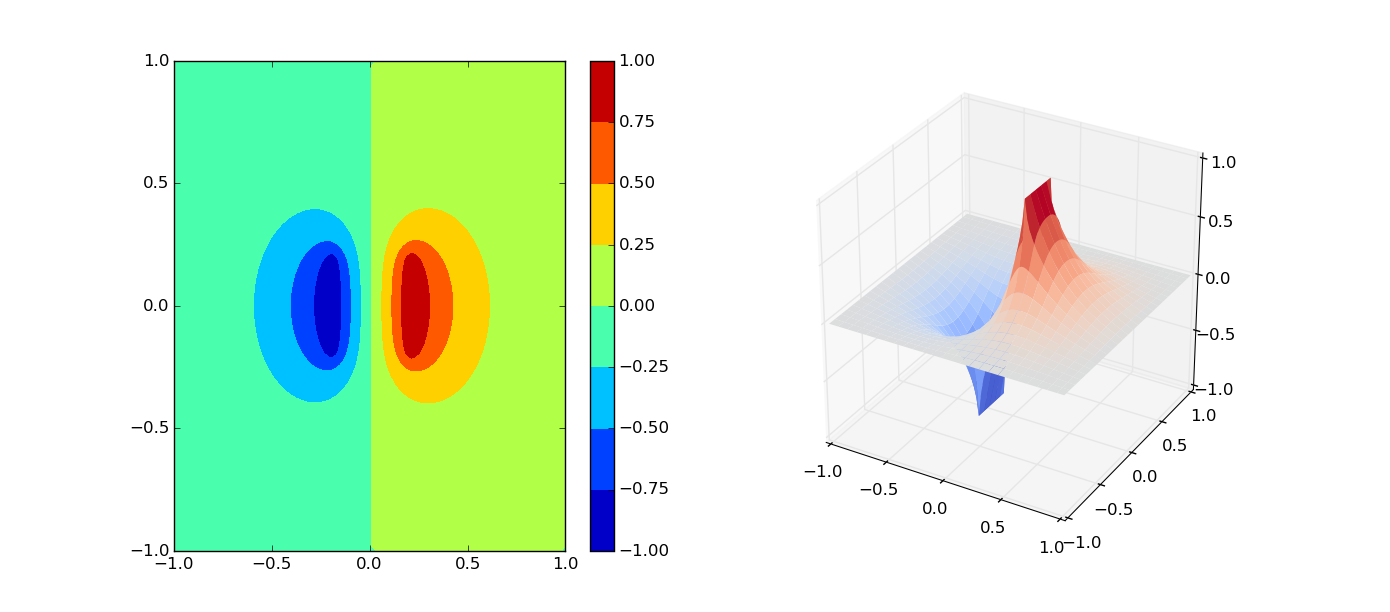
  Because the array we chosed is big, so we obtained a smoth counter plot, where different color stand for different value of potential. Look pretty beautiful! Now we know the poential distribution of the capacitor system.
• Second, there comes the point charge syatem, we know it's analytical solution is $V(r)=\frac{q}{4\pi \epsilon}$. Now, let us confirm this conclusion:
  
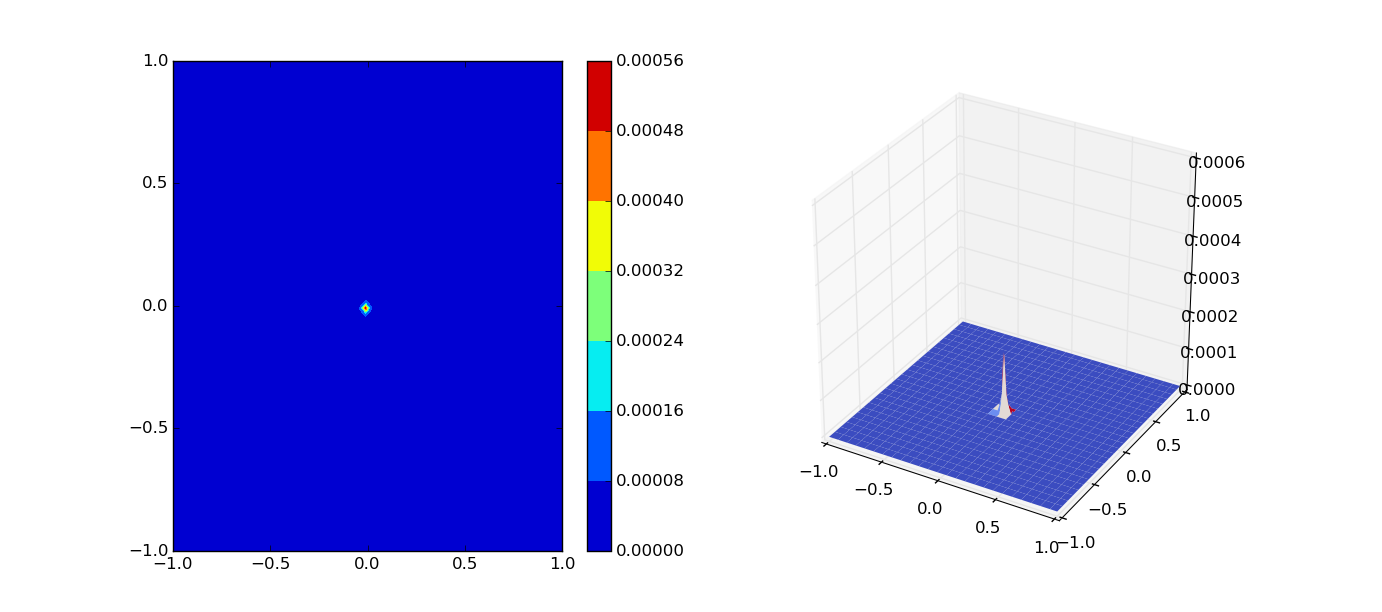
  That is the form of Coulomb's law! We now know the power of the numerrical mathod. Actually we can apply this mathod to more complicated systems where analytical ways can not work.

The conclusion:

Through the program we have Solved this two inportant partial equations, and plot beautiful figure. Most importantly, We now know how to solve partial equations numerically: finite difference of time and position. That important in following work of Computational Physics.

Finally，thanks for Guo Shuaifei.