@910935974 2019-10-11T15:58:50.000000Z 字数 15714 阅读 524

算法笔记——图论

算法 图论

最短路

Floyed
求任意两点间的最短路，最简单的三段循环，复杂度为 $O(n^3)$ 。注意先枚举中间节点。
代码：

for(int k=1;k<=n;++k)
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);

Dijkstra
求单源最短路径，复杂度为 $O(n^2)$ 或 $O(n\log n)$ 。思想是蓝白点+队列，不能判负环，可以堆优化。
代码：

#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 200005
#define maxm 800005
using namespace std;
priority_queue< pair<int,int> >qu;//堆优化dijkstra
struct node
{
    int v,val,next;
}tr[maxm],ne[maxm];
int n,m,s,e;
int tot,head[maxn];
int que[maxm];
int dis[maxn],vis[maxn];
void add(int x,int y,int z)
{
    tot++;
    tr[tot].v=y;
    tr[tot].val=z;
    tr[tot].next=head[x];
    head[x]=tot;
}
void dj()
{
    memset(dis,0x3f3f3f,sizeof(dis));
    dis[s]=0;
    qu.push(make_pair(0,s));
    while(qu.size())
    {
        int x=qu.top().second;//取出堆顶
        qu.pop();
        if(vis[x])continue;
        vis[x]=1;
        for(int t=head[x];t;t=tr[t].next)
        {
            int y=tr[t].v,z=tr[t].val;
            if(dis[y]>dis[x]+z)
            {
                dis[y]=dis[x]+z;
                qu.push(make_pair(-dis[y],y));
            }//把二元组插入堆
        }
    }
}//堆优化的dijkstra
int main()
{
    freopen("data.in","r",stdin);
    freopen("data.out","w",stdout);
    scanf("%d%d%d",&n,&m,&s);
    for(int i=1;i<=m;++i)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
    }
    dj();//dijkstra求最短路
    for(int i=1;i<=n;++i)
    printf("%d ",dis[i]);
    return 0;
}

Spfa
求单源最短路径，可以判负环，最坏复杂度 $O(mn)$ ，但容易被菊花图卡掉。
代码：

#include<cstdio>
#include<cstring>
#define ll long long
#define maxn 10005
#define maxm 500005
using namespace std;
struct node
{
    ll v,val,next;
}tr[maxm];
ll n,m,s;
ll tot,head[maxn];
ll dis[maxn],vis[maxn],q[maxm];
void add(ll x,ll y,ll z)
{
    tot++;
    tr[tot].v=y;
    tr[tot].next=head[x];
    tr[tot].val=z;
    head[x]=tot;
}
void spfa()
{
    ll top=0,hd=0;
    memset(dis,0x3f3f3f3f,sizeof(dis));
    vis[s]=1;
    dis[s]=0;
    q[++top]=s;
    while(hd<top)
    {
        int x=q[++hd];
        vis[x]=0;
        for(ll t=head[x];t;t=tr[t].next)
        {
            ll y=tr[t].v,z=tr[t].val;
            if(dis[y]>dis[x]+z)
            {
                dis[y]=dis[x]+z;
                if(!vis[y])
                {
                    q[++top]=y;
                    vis[y]=1;
                }
            }
        }
    }
}
int main()
{
    scanf("%lld%lld%lld",&n,&m,&s);
    for(ll i=1;i<=m;++i)
    {
        ll x,y,z;
        scanf("%lld%lld%lld",&x,&y,&z);
        add(x,y,z);
    }
    spfa();
    for(ll i=1;i<=n;++i)
    {
        if(dis[i]>=0x3f3f3f3f3f)
        printf("2147483647 ");
        else printf("%lld ",dis[i]);
    }
    return 0;
}

总结
如果有可能出现负环，直接用Spfa，否则首选Dijkstra堆优化。
应用
1.求最短路；
2.作为一些算法的辅助算法（如差分约束里需要用到Spfa判解）。
例题
1.【模板】单源最短路径（弱化版）；
2.【模板】单源最短路径（标准版）；
3.【模板】负环（为什么用队列就那么快？？？）；

分层图

概念
顾名思义，就是一张分成几个层次的图。
这种题一般的套路是，给出一张图，求出最短路，但是这张图中可以选取 $k$ 或者打一定的折扣。这种情况下就需要用到分层图。
方法
这里介绍两种方法：
1.与求普通的最短路大同小异，只是单源最短路的 $dis[i]$ 数组要变成 $dis[i][j]$ ，表示起点到节点 $i$ 当中花费 $j$ 条免费边的最短路径。状态转移很简单。
2.拆点法。将每个点拆成k层点，相同层的边权为 $val$ ，不同层的边权为0，最短路算法不变。
代码

1.dp法

#include<cstdio>
#include<queue>
#include<cstring>
#define maxn 10005
#define maxm 50005
#define maxk 15
using namespace std;
struct node
{
    int v,val,next;
}tr[maxm<<1];
int n,m,k,s,t;
int tot,head[maxn];
int dis[maxn][maxk];
priority_queue<pair<int,int> >que;
void add(int x,int y,int z)
{
    tot++;
    tr[tot].v=y;
    tr[tot].val=z;
    tr[tot].next=head[x];
    head[x]=tot;
}
void dijstra()
{
    memset(dis,0x3f3f3f3f,sizeof(dis));
    for(int i=0;i<=k;++i)
    dis[s][i]=0;//初始化
    for(int i=0;i<=k;++i)//枚举次数
    {
        que.push(make_pair(0,s));
        while(que.size())
        {
            int x=que.top().second;
            que.pop();
            for(int t=head[x];t;t=tr[t].next)
            {
                int y=tr[t].v,z=tr[t].val,fl=0;
                if(i)
                {
                    if(dis[y][i]>dis[x][i-1])//使用免费次数
                    {
                        dis[y][i]=dis[x][i-1];
                        fl=1;
                    }
                }
                if(dis[y][i]>dis[x][i]+z)//不使用次数
                {
                    dis[y][i]=dis[x][i]+z;
                    fl=1;
                }
                if(fl)
                que.push(make_pair(-dis[y][i],y));
            }
        }//分层图dp
    }
}//堆优化dijstra
int main()
{
    scanf("%d%d%d%d%d",&n,&m,&k,&s,&t);
    s++;t++;
    for(int i=1;i<=m;++i)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        x++;y++;
        add(x,y,z);
        add(y,x,z);
    }
    dijstra();
    printf("%d",dis[t][k]);
    return 0;
}

2.拆点法

#include<cstdio>
#include<cstring>
#include<queue>
#define maxn 1000005
#define maxm 20000005
#define maxk 25
using namespace std;
struct node
{
    int v,val,next;
}tr[maxm<<1];
int n,m,k,ans;
int tot,head[maxn];
int dis[maxn],vis[maxn];
priority_queue<pair<int,int> >que;
void add(int x,int y,int z)
{
    tot++;
    tr[tot].v=y;
    tr[tot].val=z;
    tr[tot].next=head[x];
    head[x]=tot;
}
void dijstra()
{
    memset(dis,0x3f3f3f3f,sizeof(dis));
    dis[1]=0;
    que.push(make_pair(0,1));
    while(que.size())
    {
        int x=que.top().second;
        que.pop();
        if(vis[x])continue;
        vis[x]=1;
        for(int t=head[x];t;t=tr[t].next)
        {
            int y=tr[t].v,z=tr[t].val;
            if(dis[y]>dis[x]+z)
            {
                dis[y]=dis[x]+z;
                que.push(make_pair(-dis[y],y));
            }
        }
    }
}//dijstra
int main()
{
    scanf("%d%d%d",&n,&m,&k);
    for(int i=1;i<=m;++i)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        add(x,y,z);
        add(y,x,z);
        for(int j=1;j<=k;++j)
        {
            add(j*n+x,j*n+y,z);
            add(j*n+y,j*n+x,z);//分层建图
            add((j-1)*n+x,j*n+y,0);
            add((j-1)*n+y,j*n+x,0);//每层建的权值为0
        }
    }
    dijstra();
    ans=dis[n];
    for(int i=1;i<=k;++i)
    ans=min(ans,dis[i*n+n]);
    printf("%d",ans);
    return 0;
}

个人还是喜欢dp法。
模板题：
1.[USACO09FEB]改造路Revamping Trails；
2.[JLOI2011]飞行路线；
3.[BJWC2012]冻结；

还有一种分层图可以用二分答案的方法解决，这里不细讲，给出一道例题：
电话线。

生成树

算法
Prim算法。
思想
贪心。
代码（此处是最小生成树）

#include<cstdio>
#include<algorithm>
using namespace std;
struct node
{
    int u,v,d;
}len[200005];
int m,n,fa[100005];
int find(int x)
{
    return fa[x]==x ? x : fa[x]=find(fa[x]); 
}//路径压缩
void unnion(int x,int y)
{
    x=find(x),y=find(y);
    fa[x]=y;
}
int judge(int x,int y)
{
    x=find(x),y=find(y);
    if(x==y)return 1;
    return 0;
}//手写并查集
bool cmp(node x,node y)
{
    return x.d<y.d;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    fa[i]=i;
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        len[i].u=x,len[i].v=y,len[i].d=z;
    }
    sort(len+1,len+1+m,cmp);
    int sum=0,ans=0;
    for(int i=1;i<=m;i++)
    {
        if(judge(len[i].u,len[i].v))continue;
        unnion(len[i].u,len[i].v);
        sum++;
        ans+=len[i].d;
        if(sum==n-1)
        {
            printf("%d",ans);
            return 0;
        }
    }
    if(sum==n)printf("%d",ans);
    else printf("orz");
    return 0;
}

习题
1.货车运输（最大生成树）；

差分约束

作用
解不等式组；
思想
转化为图论，通过不等关系建图。
如： $a_i-b_i\leq c_i$ 可转化为在 $a_i$ 和 $b_i$ 间建立一条长为 $c_i$ 的单项边。
代码

#include<cstdio>
#include<queue>
#include<cstring>
#define maxn 20005
#define maxm 20005
using namespace std;
struct node
{
    int v,val,next;
}tr[maxm];
int m,n;
int tot,head[maxn];
int cnt[maxn],dis[maxn],vis[maxn];
queue<int>q;
void add(int x,int y,int z)
{
    tot++;
    tr[tot].v=y;
    tr[tot].val=z;
    tr[tot].next=head[x];
    head[x]=tot;
}//建边
int spfa()
{
    memset(dis,0x3f3f3f3f,sizeof(dis));
    for(int i=1;i<=n;++i)
    {
        q.push(i);
        vis[i]=1;
    }
    dis[1]=0;
    while(q.size())
    {
        int x=q.front();
        q.pop();
        vis[x]=0;
        for(int t=head[x];t;t=tr[t].next)
        {
            int y=tr[t].v,z=tr[t].val;
            cnt[y]=cnt[x]+1;
            if(cnt[y]>n)
            return 0;//判负环
            if(dis[y]>dis[x]+z)
            {
                dis[y]=dis[x]+z;
                if(!vis[y])
                {
                    q.push(y);
                    vis[y]=1; 
                }
            }//更新最短路
        }
    }
    return 1;
}
void work1()
{
    int a,b,c;
    scanf("%d%d%d",&a,&b,&c);
    if(a==b&&c!=0)
    {
        printf("No");
        return;
    }
    add(b,a,-c);
}//a-b>=c转化为b-a<=-c
void work2()
{
    int a,b,c;
    scanf("%d%d%d",&a,&b,&c);
    if(a==b&&c!=0)
    {
        printf("No");
        return;
    }
    add(a,b,c);
}//a-b<=c
void work3()
{
    int a,b;
    scanf("%d%d",&a,&b);
    add(a,b,0);
    add(b,a,0);
}//a-b==0转化为a-b<=0&&b-a<=0 
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i)
    {
        int flag;
        scanf("%d",&flag);
        if(flag==1)
        work1();
        else if(flag==2)
        work2();
        else if(flag==3)
        work3();
    }
    if(!spfa())
    printf("No");
    else printf("Yes");
    return 0;
}

模板题：小K的农场;

拓扑排序

概念
对于一个有向图，若做事有先后顺序，可以用拓扑排序。
思想
队列或栈（大多数情况下用的是队列）。
先扫描一遍，若点 $i$ 的度数为1，入队。
结下来，对于队列中每个元素，枚举与它相连的节点 $x$ ，使 $x$ 度数减1，若 $x$ 的度数为1， $x$ 入读，以此类推。
代码

#include<bits/stdc++.h>
using namespace std;
int indgr[105],stackk[105],s[105][105],n,top=0;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int x;
        scanf("%d",&x);
        while(x!=0)
        {
            indgr[x]++;
            s[i][x]=1;
            scanf("%d",&x);
        }
    }//输入，记录入度
    for(int i=1;i<=n;i++)
    if(indgr[i]==0)
    {
        top++;
        stackk[top]=i;//初始化，将入度为0的点入栈
    }
    while(top>0)
    {
        int v=stackk[top];
        printf("%d ",v);
        top--;//顶点出栈 
        for(int j=1;j<=n;j++)
        if(s[v][j]==1)
        {
            indgr[j]--;//删除与当前顶点相连的边
            if(indgr[j]==0)stackk[++top]=j;//入栈
        }
    }
    return 0;
}

Tarjan算法及其应用

tarjan缩点
针对有向图或无向图的强连通分量，将有向图或无向图中的强联通分量缩成一个点，这样就不会因为在环中跑而TLE了，搭配拓扑排序食用绝佳。

下面给出tarjan缩点加上拓扑排序的实例。
代码：

#include<cstdio>
#define maxn 10005
#define maxm 50005
using namespace std;
struct node
{
    int v,next;
}tr[maxm];
int n,m;
int head[maxn],tot;
int out[maxn];
int stk[maxn],co[maxn],low[maxn],dfn[maxn],sum[maxn],top,col,num;
int flag,ans;
int min(int a,int b)
{
    return a<b?a:b;
}
void add(int x,int y)
{
    tot++;
    tr[tot].v=y;
    tr[tot].next=head[x];
    head[x]=tot;
}
void tarjan(int u)
{
    stk[++top]=u;
    low[u]=dfn[u]=++num;
    for(int t=head[u];t;t=tr[t].next)
    {
        int v=tr[t].v;
        if(!dfn[v])
        {
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }//更新树边
        else if(!co[v])
        {
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(low[u]==dfn[u])
    {
        co[u]=++col;
        sum[col]++;
        while(stk[top]!=u)
        {
            co[stk[top--]]=col;
            sum[col]++;//统计联通块中的元素个数
        }
        top--;
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
    }
    for(int i=1;i<=n;++i)
    {
        if(!dfn[i])
        tarjan(i);
    }
    for(int i=1;i<=n;++i)
    {
        for(int t=head[i];t;t=tr[t].next)
        {
            int v=tr[t].v;
            if(co[i]!=co[v])
            out[co[i]]++;//统计出度
        }
    }//建新图
    for(int i=1;i<=col;++i)
    {
        if(out[i]==0)
        {
            if(flag==1)
            {
                printf("0");
                return 0;
            }
            else
            {
                flag=1;
                ans=sum[i];
            }
        }
    }
    printf("%d",ans);
    return 0;
}

模板题：【模板】缩点；

tarjan割点（V-DCC）

所谓割点，即图中的一个点，去掉这个点和这个点所连的边后，能将图分成两个部分。
找割点的代码：

#include<cstdio>
#define maxn 5005
using namespace std;
struct node
{
    int v,next;
}tr[maxn<<1];
int n,m;
int tot,head[maxn];
int timer,ans,root,dfn[maxn],low[maxn],cut[maxn];//dfn[x]是x的dfs序,low[x]是x可以扫到的dfs序最小的节点
int min(int x,int y)
{
    return x<y?x:y;
}
void add(int x,int y)
{
    tot++;
    tr[tot].v=y;
    tr[tot].next=head[x];
    head[x]=tot;
}//建图
void tarjan(int u)
{
    dfn[u]=low[u]=++timer;//初始化更新时间戳
    int tot=0;
    for(int t=head[u];t;t=tr[t].next)
    {
        int y=tr[t].v;
        if(!dfn[y])
        {
            tarjan(y);
            low[u]=min(low[u],low[y]);//更新low[u]
            if(low[y]>=dfn[u])
            {
                tot++;
                if(u!=root||tot>=2)
                cut[u]=1;//找到割点
            }//x可以把图分成两个不连通的部分
        }//若y未被扫描过则去扫描y
        else low[u]=min(low[u],dfn[y]);//更新low[x]
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }
    for(int i=1;i<=n;++i)
    {
        if(!dfn[i])
        {
            root=i;
            tarjan(i);
        }
    }//扫描割点
    for(int i=1;i<=n;++i)
    {
        if(cut[i])
        ans++;
    }
    printf("%d",ans);
    return 0;
}

tarjan割边

割边，就是桥，即若去掉桥，则该图不连通。
代码：

#include<cstdio>
#define maxn 50005
using namespace std;
struct node
{
    int v,next;
}tr[maxn<<1];
int n,m;
int tot,head[maxn];
int timer,ans,bridge[maxn<<1],dfn[maxn],low[maxn];
int min(int x,int y)
{
    return x<y?x:y;
}
void add(int x,int y)
{
    tot++;
    tr[tot].v=y;
    tr[tot].next=head[x];
    head[x]=tot;
}//建图
void tarjan(int u,int in_edge)
{
    dfn[u]=low[u]=++timer;
    for(int t=head[u];t;t=tr[t].next)
    {
        int y=tr[t].v;
        if(!dfn[y])
        {
            tarjan(y,t);
            low[u]=min(low[u],low[y]);
            if(low[y]>dfn[u])
            bridge[t]=bridge[t^1]=1;//标记割边(需标记双向边)
        }
        else if(t!=(in_edge^1))
        low[u]=min(low[u],dfn[y]);//我也看不懂QAQ
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    tot=1;
    for(int i=1;i<=m;++i)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }
    for(int i=1;i<=n;++i)
    {
        if(!dfn[i])
        tarjan(i,0);
    }
    for(int i=2;i<tot;i+=2)
    {
        if(bridge[i])
        ans++;
    }
    printf("%d",ans);
    return 0;
}

因为以上内容均为省选内容，所以我说的比较简略（其实是我看不懂）。

2-sat

安利博客：2-sat思想及入门；
所以，，，上代码：

#include<cstdio>
#define maxn 2000005
using namespace std;
struct node
{
    int v,next;
}tr[maxn<<1];
int n,m;
int tot,head[maxn];
int timer,col,top,stk[maxn],dfn[maxn],low[maxn],co[maxn],vis[maxn];//tarjan判是否成立,求拓扑序列
int ans[maxn];
int min(int x,int y)
{
    return x<y?x:y;
}
void add(int x,int y)
{
    tot++;
    tr[tot].v=y;
    tr[tot].next=head[x];
    head[x]=tot;
}
void tarjan(int x)
{
    stk[++top]=x;
    dfn[x]=low[x]=++timer;
    for(int t=head[x];t;t=tr[t].next)
    {
        int y=tr[t].v;
        if(!dfn[y])
        {
            tarjan(y);
            low[x]=min(low[x],low[y]);
        }
        else if(!co[y])
        low[x]=min(low[x],dfn[y]);
    }
    if(dfn[x]==low[x])
    {
        co[x]=++col;
        while(stk[top]!=x)
        {
            co[stk[top]]=col;
            top--;
        }
        top--;
    }//成环
}//tajan求强连通分量和反着的拓扑序
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i)
    {
        int x,xx,y,yy;
        scanf("%d%d%d%d",&x,&xx,&y,&yy);
        add(x+n*(xx&1),y+n*(yy^1));
        add(y+n*(yy&1),x+n*(xx^1));//位运算优化
    }//x为真,x+n为假
    for(int i=1;i<=2*n;++i)
    {
        if(!dfn[i])
        tarjan(i);
    }
    for(int i=1;i<=n;++i)
    {
        if(co[i]==co[i+n])
        {
            printf("IMPOSSIBLE");
            return 0;
        }
    }//i和i+n在同一个强连通分量里
    printf("POSSIBLE\n");
    for(int i=1;i<=n;++i)
    printf("%d ",co[i]<co[i+n]);
    return 0;
}
/*
if (va && vb)
{ // a, b 都真，-a -> b, -b -> a
    g[a + n].push_back(b);
    g[b + n].push_back(a);
}
else if (!va && vb)
{ // a 假 b 真，a -> b, -b -> -a
    g[a].push_back(b);
    g[b + n].push_back(a + n);
}
else if (va && !vb)
{ // a 真 b 假，-a -> -b, b -> a
    g[a + n].push_back(b + n);
    g[b].push_back(a);
}
else if (!va && !vb)
{ // a, b 都假，a -> -b, b -> -a
    g[a].push_back(b + n);
    g[b].push_back(a + n);
}
*/

习题：
1.【模板】2-SAT 问题；
2.[JSOI2010]满汉全席；

二分图

概念
把一张图分成两个区间，同一个区间内不能连边，这样的图就是二分图。
像这样：
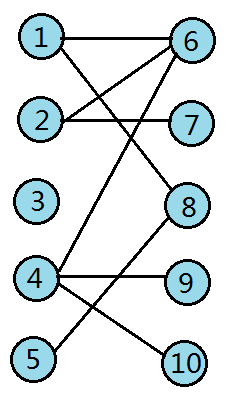
二分图的匹配
左边一个连右边一个，且每个节点只能被匹配一次，这就是二分图的匹配。
匈牙利算法
1.作用
求二分图最大匹配。
2.流程
不断寻找增广路，直到找不到为止，就求出了二分图的最大匹配。（注意，建图时最好建立单向边）
代码

#include<cstdio>
#include<cstring>
using namespace std;
#define maxn 405
#define maxm 60005
struct node
{
    int v,next;
}tr[maxm];
int match[maxn],head[maxn],vis[maxn];
int n,p,cnt,tot,timer;
void add(int x,int y)
{
    tot++;
    tr[tot].v=y;
    tr[tot].next=head[x];
    head[x]=tot;
}
int dfs(int x)//找增广路
{
    for(int t=head[x];t;t=tr[t].next)
    {
        int y=tr[t].v;
        if(vis[y]==timer) continue;
        vis[y]=timer;
        if(!match[y]||dfs(match[y]))
        {
            match[y]=x;
            return 1;
        }
    }
    return 0;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        tot=0;
        scanf("%d%d",&p,&n);
        for(int i=1;i<=p;i++)
        {
            scanf("%d",&cnt);
            while(cnt--)
            {
                int x;
                scanf("%d",&x);
                add(i,p+x);
            }//建立二分图
        }
        int ans=0;
        for(int i=1;i<=p;i++)
        {
            timer++;
            if(dfs(i))ans++;
        }
        if(ans==p)
        printf("YES\n");
        else printf("NO\n");
        for(int i=1;i<=p+n;++i)head[i]=0;
        for(int i=1;i<=p+n;++i)match[i]=0;
    }
    return 0;
}

习题
1.【模板】二分图匹配；
2.[NOI2009]变换序列；
3.[HEOI2016/TJOI2016]游戏；

网络流

因为种类太多，所以直接给模板了。
- 最大流（最小割）

#include<cstdio>
#include<cstring>
#define maxn 10005
#define maxm 200005
using namespace std;
struct node
{
    int v,val,next;
}tr[maxm];
int n,m,s,e;
int tot=1,head[maxn];//从2开始存，保证异或
int timer,dis[maxn],qu[maxm],vis[maxn];
int min(int a,int b)
{
    return a<b?a:b; 
}
void add(int x,int y,int z)
{
    tot++;
    tr[tot].v=y;
    tr[tot].val=z;
    tr[tot].next=head[x];
    head[x]=tot;
} 
void Add(int x,int y,int z)
{
    add(x,y,z);
    add(y,x,0);
}
int bfs()
{
    int hd=0,top=0;
    qu[++top]=s;
    dis[s]=0;
    vis[s]=++timer;//起点入队,timer判断入队时间
    while(hd<top)
    {
        int x=qu[++hd];
        for(int t=head[x];t!=-1;t=tr[t].next)
        {
            int y=tr[t].v,z=tr[t].val;
            if(z==0)continue;
            if(vis[y]!=timer)
            {
                vis[y]=timer;
                dis[y]=dis[x]+1;
                qu[++top]=y;
            }//拓展节点,寻找增广路
        }
    }
    return vis[e]==timer;//找到增广路返回1,反之返回2
}
int dfs(int x,int lim)
{
    if(x==e)return lim;//到达终点
    int ans=0;
    for(int t=head[x];t!=-1;t=tr[t].next)
    {
        int y=tr[t].v,z=tr[t].val;
        if(z!=0&&dis[y]==dis[x]+1)//有流量且相连
        {
            int nw=dfs(y,min(z,lim));
            if(nw!=0)
            {
                tr[t].val-=nw;
                tr[t^1].val+=nw;
                lim-=nw;
                ans+=nw;
                if(lim==0)
                return ans;
            }   
        }
    }
    return ans;
}
int dinic()
{
    int ans=0;
    while(bfs())ans+=dfs(s,0x3f3f3f3f);
    return ans;
}
int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d%d%d",&n,&m,&s,&e);
    for(int i=1;i<=m;i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        Add(x,y,z);
    }
    printf("%d",dinic());
    return 0;
}

模板：
1.【模板】网络最大流；
2.酒店之王；

费用流
最小费用最大流：

#include<cstdio>
#include<algorithm>
#include<cstring>
#define inf 0x3f3f3f3f
#define maxn 50005
#define maxm 150005
using namespace std;
struct node
{
    int u,v,next,val,cost;
}tr[maxm];
int tot=1,head[maxn];
int hd,tp,que[maxm<<2],dis[maxn],in[maxn],pre[maxn];//建队
int n,m,s,t;
int ans,ans2;
void add(int x,int y,int w,int va)
{
    tot++;
    tr[tot].u=x;
    tr[tot].v=y;
    tr[tot].next=head[x];
    tr[tot].val=w;
    tr[tot].cost=va;
    head[x]=tot;
}//建边
void Add(int x,int y,int w,int va)
{
    add(x,y,w,va);
    add(y,x,0,-va);//建立反向边,注意单位费用为-va
}
void spfa()
{
    memset(dis,inf,sizeof(dis));
    memset(que,0,sizeof(que));
    memset(in,0,sizeof(in));
    hd=tp=0;
    dis[s]=0;
    que[++tp]=s;
    in[s]=1;//初始化队列
    while(hd<tp)
    {
        int x=que[++hd];
        in[x]=0;
        for(int i=head[x];i!=-1;i=tr[i].next)
        {
            int y=tr[i].v;
            if(tr[i].val&&dis[y]>dis[x]+tr[i].cost)
            {
                pre[y]=i;//记录y连接的边
                dis[y]=dis[x]+tr[i].cost;
                if(!in[y])
                {
                    que[++tp]=y;
                    in[y]=1;
                }//将y入队,标记节点
            }//更新费用的最短路
        }
    }
}//spfa求增广路
void price()
{
    while(spfa(),dis[t]<inf)
    {
        int nw=inf;
        for(int i=pre[t];i;i=pre[tr[i].u])
        nw=min(nw,tr[i].val);//求出最小剩余流量
        ans+=dis[t]*nw;
        ans2+=nw;
        for(int i=pre[t];i;i=pre[tr[i].u])
        {
            tr[i].val-=nw;
            tr[i^1].val+=nw;
        }
    }
}//求出最小费用
int main()
{
    memset(head,-1,sizeof(head));
    scanf("%d%d%d%d",&n,&m,&s,&t);
    for(int i=1;i<=m;++i)
    {
        int x,y,w,va;
        scanf("%d%d%d%d",&x,&y,&w,&va);
        Add(x,y,w,va);
    }
    price();//求费用流
    printf("%d %d",ans2,ans);
    return 0;
}

模板：【模板】最小费用最大流；

无源汇可行流
有源汇可行流

线段树优化建图

因为是写了博客的，所以不细讲，直接见博客吧！
线段树优化建图
- 代码

#include<cstdio>
#include<algorithm>
#define maxn 4000005
#define lid ls[k]
#define rid rs[k]
using namespace std;
struct node
{
    int v,next;
}tr[maxn*10];
int n,m,rt,ndnum,ans;
int id[maxn],dp[maxn],nw[maxn],in[maxn];
int ls[maxn*4],rs[maxn*4],fl[maxn*4];//线段树
int tot,head[maxn];
int hd,top,que[maxn];
void add(int x,int y)
{
    tot++;
    tr[tot].v=y;
    tr[tot].next=head[x];
    head[x]=tot;
    in[y]++;//统计入度
}
void build(int &k,int l,int r)
{
    if(l==r)
    {
        k=l;
        return;
    }
    k=++ndnum;//传新编号
    int mid=(l+r)>>1;
    build(lid,l,mid);
    build(rid,mid+1,r);//下传左右儿子
    add(lid,k);
    add(rid,k);//向父节点连边
}
void addtr(int k,int L,int R,int l,int r)
{
    if(L>=l&&R<=r)
    {
        add(k,ndnum);//等级小连等级大
        return;
    }
    int mid=(L+R)>>1;
    if(l<=mid)
    addtr(lid,L,mid,l,r);
    if(r>mid)
    addtr(rid,mid+1,R,l,r);
}//线段树优化建边
void topusort()
{
    for(int i=1;i<=ndnum;++i)
    {
        if(!in[i])
        {
            que[++top]=i;
            if(i<=n)dp[i]=1;//赋初值
        }
    }
    while(hd<top)
    {
        int x=que[++hd];
        ans=max(ans,dp[x]);
        for(int t=head[x];t;t=tr[t].next)
        {
            int y=tr[t].v;
            dp[y]=max(dp[y],dp[x]+(y<=n));//状态转移
            in[y]--;
            if(!in[y])
            que[++top]=y;
        }
    }
}
int main()
{
    freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);
    scanf("%d%d",&n,&m);
    ndnum=n;//从n开始建边
    build(rt,1,n);
    for(int i=1;i<=m;++i)
    {
        int x;
        scanf("%d",&x);
        ndnum++;//建虚点
        for(int j=1;j<=x;++j)
        {
            scanf("%d",&nw[j]);
            add(ndnum,nw[j]);
        }
        for(int j=1;j<x;++j)
        {
            if(nw[j]+1!=nw[j+1])
            addtr(n+1,1,n,nw[j]+1,nw[j+1]-1);//线段树优化建边(等级小连等级大)
        }
    }
    topusort();
    printf("%d",ans);
    return 0;
}

对应例题：
车站分级