Red-Black Trees

learning

1. properties of red-black trees

1. Every node is either red or black.
2. The root is black.
3. Every leaf (NIL) is black.
4. If a node is red, then both its children are black.
5. For each node, all simple paths from the node to descendant leaves contain the same number of balck nodes.

Lemma: A red-black tree with internal nodes has height at most $2lg(n+1)$

Proof: 当 internal nodes 全为黑时，internal nodes 的数目为 $2^0+2^1+ ... +2^{bh(x)-1}=2^{bh(x)}-1$ ,也就是说，一颗红黑树至少有$2^{bh(x)}-1$个 internal nodes 。由性质4得，当黑节点数目一定时，要使得 internal nodes 数目最多，则父节点与子节点的颜色红黑相间，也就是说，从根节点到叶节点（不包括根节点）的任何一条简单路径上都至少有一半的节点为黑色。所以，$n\ge2^{h/2}-1$（其中，h为树的高度）。化简得，$h\le2lg(n+1)$

2. Rotation

• LEFT-ROTATION

/* 
 * 对红黑树的节点(x)进行左旋转
 *
 * 左旋示意图(对节点x进行左旋)：
 *      px                              px
 *     /                               /
 *    x                               y                
 *   /  \      --(左旋)-->           / \                #
 *  lx   y                          x  ry     
 *     /   \                       /  \
 *    ly   ry                     lx  ly  
 *
 *
 */
template <class T>
void RBTree<T>::leftRotate(RBTNode<T>* &root, RBTNode<T>* x)
{
    // 设x的右孩子为y
    RBTNode<T> *y = x->right;
    // 将y的左孩子设为x的右孩子
    // 如果y的左孩子非空，将x设为y的左孩子的父亲
    x->right = y->left;
    if (y->left != NULL)
        y->left->parent = x;
    // 将 “x的父亲” 设为 “y的父亲”
    y->parent = x->parent;
    if (x->parent == NULL)
    {
        root = y;            
        // 如果 “x的父亲” 是空节点，则将y设为根节点
    }
    else
    {
        if (x->parent->left == x)
            x->parent->left = y;  
    // 如果x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
        else
            x->parent->right = y; 
  // 如果x是它父节点的左孩子，则将y设为“x的父节点的左孩子”
    }
    // 将 “x” 设为 “y的左孩子”
    y->left = x;
    // 将 “x的父节点” 设为 “y”
    x->parent = y;
}

• RIGHT-ROTATION
  

/* 
 * 对红黑树的节点(y)进行右旋转
 *
 * 右旋示意图(对节点y进行左旋)：
 *            py                               py
 *           /                                /
 *          y                                x                  
 *         /  \      --(右旋)-->            /  \                     #
 *        x   ry                           lx   y  
 *       / \                                   / \                   #
 *      lx  rx                                rx  ry
 * 
 */
template <class T>
void RBTree<T>::rightRotate(RBTNode<T>* &root, RBTNode<T>* y)
{
    // 设置x是当前节点的左孩子。
    RBTNode<T> *x = y->left;
    // 将 “x的右孩子” 设为 “y的左孩子”；
    // 如果"x的右孩子"不为空的话，将 “y” 设为 “x的右孩子的父亲”
    y->left = x->right;
    if (x->right != NULL)
        x->right->parent = y;
    // 将 “y的父亲” 设为 “x的父亲”
    x->parent = y->parent;
    if (y->parent == NULL) 
    {
        root = x;           
        // 如果 “y的父亲” 是空节点，则将x设为根节点
    }
    else
    {
        if (y == y->parent->right)
            y->parent->right = x;    
            // 如果y是它父节点的右孩子，则将x设为“y的父节点的右孩子”
        else
            y->parent->left = x;   
            // (y是它父节点的左孩子) 将x设为“x的父节点的左孩子”
    }
    // 将 “y” 设为 “x的右孩子”
    x->right = y;
    // 将 “y的父节点” 设为 “x”
    y->parent = x;
}

3.Insertion

• Insert node z into the tree as if it were an ordinary binary search tree.
• color z red.
• call an auxiliary procedure RB-INSERT-FIXUP to recolor nodes and perform rotations.

/* 
 * 参数说明：
 *     root 红黑树的根结点
 *     node 插入的结点        // 对应《算法导论》中的node
 */
template <class T>
void RBTree<T>::insert(RBTNode<T>* &root, RBTNode<T>* node)
{
    RBTNode<T> *y = NULL;
    RBTNode<T> *x = root;
    /*1. Insert node z into the tree as if it were an ordinary binary search tree*/
    while (x != NULL)
    {
        y = x;
        if (node->key < x->key)
            x = x->left;
        else
            x = x->right;
    }
    node->parent = y;
    if (y!=NULL)
    {
        if (node->key < y->key)
            y->left = node;
        else
            y->right = node;
    }
    else
        root = node;
    // 2. color z red
    node->color = RED;
    /* 3. call an auxiliary procedure RB—INSERT-FIXUP to recolor nodes and perform rotations*/
    insertFixUp(root, node);
}

• case 1: z's uncle y is red

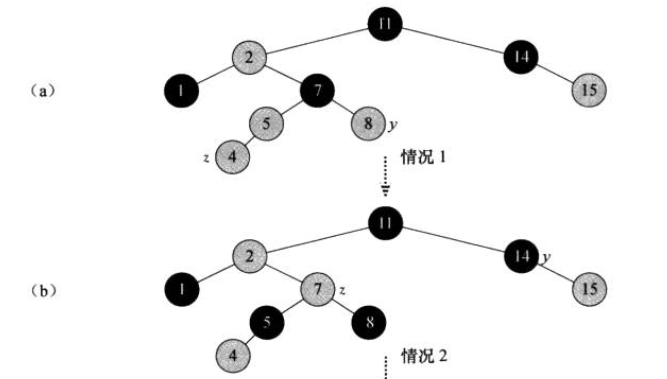
• case 2: z's uncle y is black and z is a right child

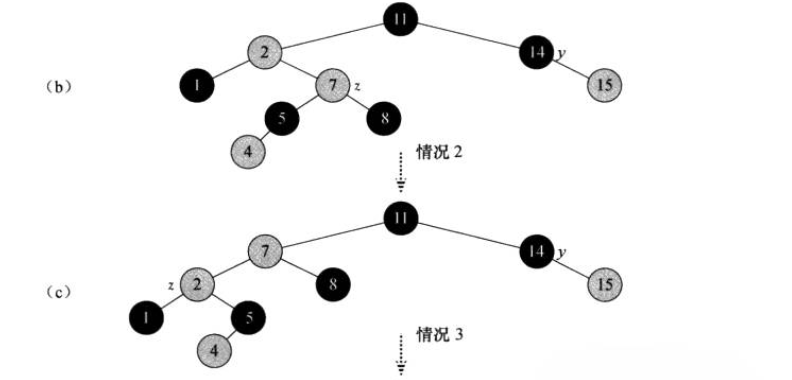
• case 3: z's uncle y is black and z is a left child

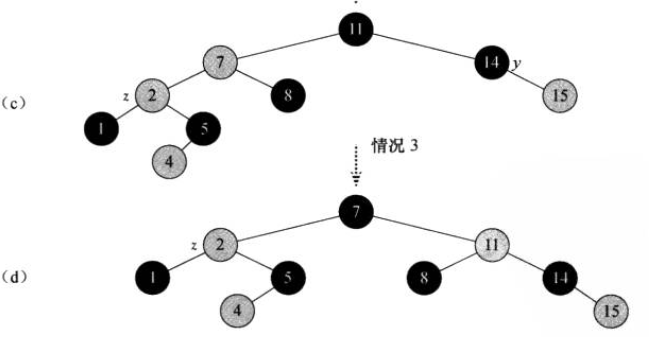
Same as then clause with "right" and "left" exchanged.

*
 * 红黑树插入修正函数
 *
 * 在向红黑树中插入节点之后(失去平衡)，再调用该函数；
 * 目的是将它重新塑造成一颗红黑树。
 *
 * 参数说明：
 *     root 红黑树的根
 *     node 插入的结点        // 对应《算法导论》中的z
 */
template <class T>
void RBTree<T>::insertFixUp(RBTNode<T>* &root, RBTNode<T>* node)
{
    RBTNode<T> *parent, *gparent;
    // 若“父节点存在，并且父节点的颜色是红色”
    while ((parent = rb_parent(node)) && rb_is_red(parent))
    {
        gparent = rb_parent(parent);
        //若“父节点”是“祖父节点的左孩子”
        if (parent == gparent->left)
        {
            // Case 1 z's uncle y is red
            {
                RBTNode<T> *uncle = gparent->right;
                if (uncle && rb_is_red(uncle))
                {
                    rb_set_black(uncle);
                    rb_set_black(parent);
                    rb_set_red(gparent);
                    node = gparent;
                    continue;
                }
            }
          // Case 2 z's uncle y is black and z is a right child
            if (parent->right == node)
            {
                RBTNode<T> *tmp;
                leftRotate(root, parent);
                tmp = parent;
                parent = node;
                node = tmp;
            }
     // Case 3 z's uncle y is black and z is a left child
            rb_set_black(parent);
            rb_set_red(gparent);
            rightRotate(root, gparent);
        } 
        else//若“z的父节点”是“z的祖父节点的右孩子”
        {
            // Case 1 z's uncle y is red
            {
                RBTNode<T> *uncle = gparent->left;
                if (uncle && rb_is_red(uncle))
                {
                    rb_set_black(uncle);
                    rb_set_black(parent);
                    rb_set_red(gparent);
                    node = gparent;
                    continue;
                }
            }
            // Case 2 z's uncle y is black and z is a left child
            if (parent->left == node)
            {
                RBTNode<T> *tmp;
                rightRotate(root, parent);
                tmp = parent;
                parent = node;
                node = tmp;
            }
         // Case 3 z's uncle y is black and z is a right child
            rb_set_black(parent);
            rb_set_red(gparent);
            leftRotate(root, gparent);
        }
    }
    // color root node black
    rb_set_black(root);
}

4. Deletion

• Delete node z into the tree as if it were an ordinary binary search tree.
• call an auxiliary procedure RB-DELETE-FIXUP to recolor nodes and perform rotations.

/* 
 * 参数说明：
 *     root 红黑树的根结点
 *     node 删除的结点
 */
template <class T>
void RBTree<T>::remove(RBTNode<T>* &root, RBTNode<T> *node)
{
    RBTNode<T> *child, *parent;
    RBTColor color;
    // 被删除节点的"左右孩子都不为空"的情况。
    if ( (node->left!=NULL) && (node->right!=NULL) ) 
    {
        // 被删节点的后继节点。(称为"取代节点")
        // 用它来取代"被删节点"的位置，然后再将"被删节点"去掉。
        RBTNode<T> *replace = node;
        // 获取后继节点
        replace = replace->right;
        while (replace->left != NULL)
            replace = replace->left;
        // "node节点"不是根节点(只有根节点不存在父节点)
        if (rb_parent(node))
        {
            if (rb_parent(node)->left == node)
                rb_parent(node)->left = replace;
            else
                rb_parent(node)->right = replace;
        } 
        else 
            // "node节点"是根节点，更新根节点。
            root = replace;
        // child是"取代节点"的右孩子，也是需要"调整的节点"。
        // "取代节点"肯定不存在左孩子！因为它是一个后继节点。
        child = replace->right;
        parent = rb_parent(replace);
        // 保存"取代节点"的颜色
        color = rb_color(replace);
        // "被删除节点"是"它的后继节点的父节点"
        if (parent == node)
        {
            parent = replace;
        } 
        else
        {
            // child不为空
            if (child)
                rb_set_parent(child, parent);
            parent->left = child;
            replace->right = node->right;
            rb_set_parent(node->right, replace);
        }
        replace->parent = node->parent;
        replace->color = node->color;
        replace->left = node->left;
        node->left->parent = replace;
        if (color == BLACK)
            removeFixUp(root, child, parent);
        delete node;
        return ;
    }
    if (node->left !=NULL)
        child = node->left;
    else 
        child = node->right;
    parent = node->parent;
    // 保存"取代节点"的颜色
    color = node->color;
    if (child)
        child->parent = parent;
    // "node节点"不是根节点
    if (parent)
    {
        if (parent->left == node)
            parent->left = child;
        else
            parent->right = child;
    }
    else
        root = child;
    if (color == BLACK)
        removeFixUp(root, child, parent);
    delete node;
}

/*
 * 红黑树删除修正函数
 *
 * 在从红黑树中删除插入节点之后(红黑树失去平衡)，再调用该函数；
 * 目的是将它重新塑造成一颗红黑树。
 *
 * 参数说明：
 *     root 红黑树的根
 *     node 待修正的节点
 */
template <class T>
void RBTree<T>::removeFixUp(RBTNode<T>* &root, RBTNode<T> *node, RBTNode<T> *parent)
{
    RBTNode<T> *other;
    while ((!node || rb_is_black(node)) && node != root)
    {
        if (parent->left == node)
        {
            other = parent->right;
            if (rb_is_red(other))
            {
             // Case 1 x's sibling w is red
                rb_set_black(other);
                rb_set_red(parent);
                leftRotate(root, parent);
                other = parent->right;
            }
            if ((!other->left || rb_is_black(other->left)) &&
                (!other->right || rb_is_black(other->right)))
            {
            /*Case 2 x's sibling w is black, and both of w's children are black*/            
                rb_set_red(other);
                node = parent;
                parent = rb_parent(node);
            }
            else
            {
                if (!other->right || rb_is_black(other->right))
                {
                   /* Case 3 x's sibling w is black, w's left child is red, and w's right child is black*/
                    rb_set_black(other->left);
                    rb_set_red(other);
                    rightRotate(root, other);
                    other = parent->right;
                }
  /* Case 4 x's sibling w is black, and w's right child is red*/
                rb_set_color(other, rb_color(parent));
                rb_set_black(parent);
                rb_set_black(other->right);
                leftRotate(root, parent);
                node = root;
                break;
            }
        }
        else
        {
            other = parent->left;
            if (rb_is_red(other))
            {
                // Case 1 x's sibling w is red
                rb_set_black(other);
                rb_set_red(parent);
                rightRotate(root, parent);
                other = parent->left;
            }
            if ((!other->left || rb_is_black(other->left)) &&
                (!other->right || rb_is_black(other->right)))
            {
            /*Case 2 x's sibling w is black, and both of w's children are black*/
                rb_set_red(other);
                node = parent;
                parent = rb_parent(node);
            }
            else
            {
                if (!other->left || rb_is_black(other->left))
                {
                    /* Case 3 x's sibling w is black, w's right child is red, and w's left child is black*/
                    rb_set_black(other->right);
                    rb_set_red(other);
                    leftRotate(root, other);
                    other = parent->left;
                }
                /* Case 4 x's sibling w is black, and w's left child is red*/
                rb_set_color(other, rb_color(parent));
                rb_set_black(parent);
                rb_set_black(other->left);
                rightRotate(root, parent);
                node = root;
                break;
            }
        }
    }
    if (node)
        rb_set_black(node);
}