CodeCraft-21 and Codeforces Round #711 (Div. 2)

codeforces

A.GCD Sum

题意:

给你一个n,求出大于等于n的第一个满足gcd(x,Sum of digits of x)>1的数。

Solution:

考虑3的倍数，对于3的倍数一定满足上述条件。故每三个数有一个满足，暴力

#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline bool ck(ll x){
    ll sum=0;
    ll tmp=x;
    while(x) {
        sum+=x%10;x/=10;
    }
    return __gcd(tmp,sum)==1;
}
int main(){
    int n;
    scanf("%d",&n);
    long long x;
    for(int i=1;i<=n;i++){
        scanf("%lld",&x);
        for(ll i=x;i;i++) if(!ck(i)){
             printf("%lld\n",i);
             break;
        }
    }
}

B.Box Fitting

题意:

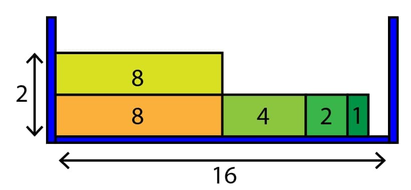
给你一个宽为W的盒子和一些高为1，宽为2^x的矩形，矩形不能重叠，问盒子至少为多高可以放下所有矩形

Solution:

直接贪心，每一层放最大的，当放不下时就要新开一层。同时可以用一个优先队列记录当前每一层剩余宽度，这样保证每次找到的剩余宽度最大。

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+7;
int n,W,w[N],ans;
priority_queue<int> q;
inline bool cmp(int a,int b){
    return a>b;
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&W);
        ans=0;
        while(!q.empty()) q.pop();
        for(int i=1;i<=n;i++) scanf("%d",&w[i]);
        sort(w+1,w+1+n,cmp);
        for(int i=1;i<=n;i++){
            if(q.empty()) {
                q.push(W);
                ans++;
            }
            if(q.top()<w[i]){
                ans++;
                q.push(W);
            }
            int x=q.top()-w[i];
            q.pop();
            q.push(x);
        }
        cout<<ans<<endl;
    }
}

C. Planar Reflections

题意:

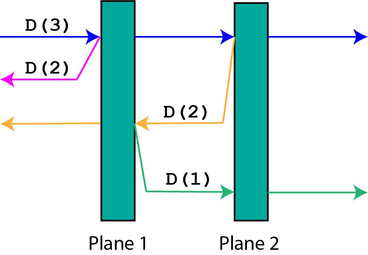
有n架飞机和一个寿命为k的粒子，当粒子撞上飞机且寿命不为1时，他会产生一个方向相反的寿命为k-1的粒子，自己寿命不变并继续保持原方向穿过飞机。给你飞机数量n，k，问最后有多少个粒子。

Solution

dp，设计状态dp[i][j][d]为寿命为j的粒子以方向d撞向第i个飞机所能产生的粒子数。
How to update the DP states? If k=1, the value of dpn[d] for any n or d is obviously 1 (as no copies are produced).

So, let us consider a particle P with k>1. This particle P produces a copy P′ going in the opposite direction. We can count the number of particles produced by P′ as dp[n — 1][k — 1][1 — d], as it hits the previous plane with a smaller decay age and in the opposite direction. Moreover, the particle P itself hits the next plane and continues to produce more stuff. We can calculate its number of particles produced as dp[n + 1][k][d], as it hits the next plane with the same decay age and the same direction!

Finally, we can combine these two values to get the value of dp[n][k][d].

#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
const int N = 1001;
const int K = 1001;
int n, k;
const int mod = 1e9 + 7;
int dp[N][K][2];
int solve(int curr, int k, int dir) {
    if (k == 1) {
        return 1;
    }
    if (dp[curr][k][dir] != -1) {
        return dp[curr][k][dir];
    }
    int ans = 2;  // me and my copy
    if (dir == 1) {
        if (curr < n)
            ans += solve(curr + 1, k, dir) — 1;
        ans %= mod;
        if (curr > 1)
            ans += solve(curr — 1, k — 1, 1 — dir) — 1;
        ans %= mod;
        dp[curr][k][dir] = ans;
    } else {
        if (curr > 1)
            ans += solve(curr — 1, k, dir) — 1;
        ans %= mod;
        if (curr < n)
            ans += solve(curr + 1, k — 1, 1 — dir) — 1;
        ans %= mod;
        dp[curr][k][dir] = ans;
    }
    return ans;
}
int main() {
    int t;
    cin >> t;
    while (t--) {
        cin >> n >> k;
        memset(dp, -1, sizeof(dp));
        cout << solve(1, k, 1) << endl;
    }
}