@Duanxx
2016-12-30T02:10:44.000000Z
字数 9365
阅读 4280
BP神经网络
神经网络&深度学习
@author : duanxxnj@163.com
@time: 2016-11-15
之前已经对感知机有了详细的解释,但是感知机只能解决线性可分的二分类问题。如果要做多分类的非线性可分问题,感知机就力不从心了。但是如果能够将感知机机连接在一起,形成一个网络的话,基于这个网络就可以实现非线性的多分类问题,这就是神经网络。
一个神经网络大致就是下面这个形式,下图所示的就是一个是三层的神经网络的示意图,其主要包括输入层(Input layer),隐藏层(Hidden layer),输出层(Output layer)。每一层都可以有多个神经元,神经网络也可以有多个隐藏层。
----------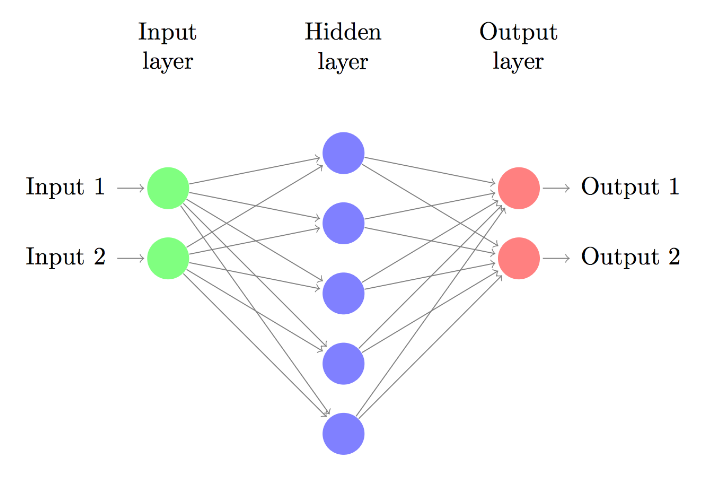
对于输入层和输出层而言,其神经元的个数基本上是定的。输入层神经元的个数和输入特征向量的维度一致;输出层的维度和待分类的类别的数据相同。决定神经网络复杂度的主要就是隐藏层的维度。
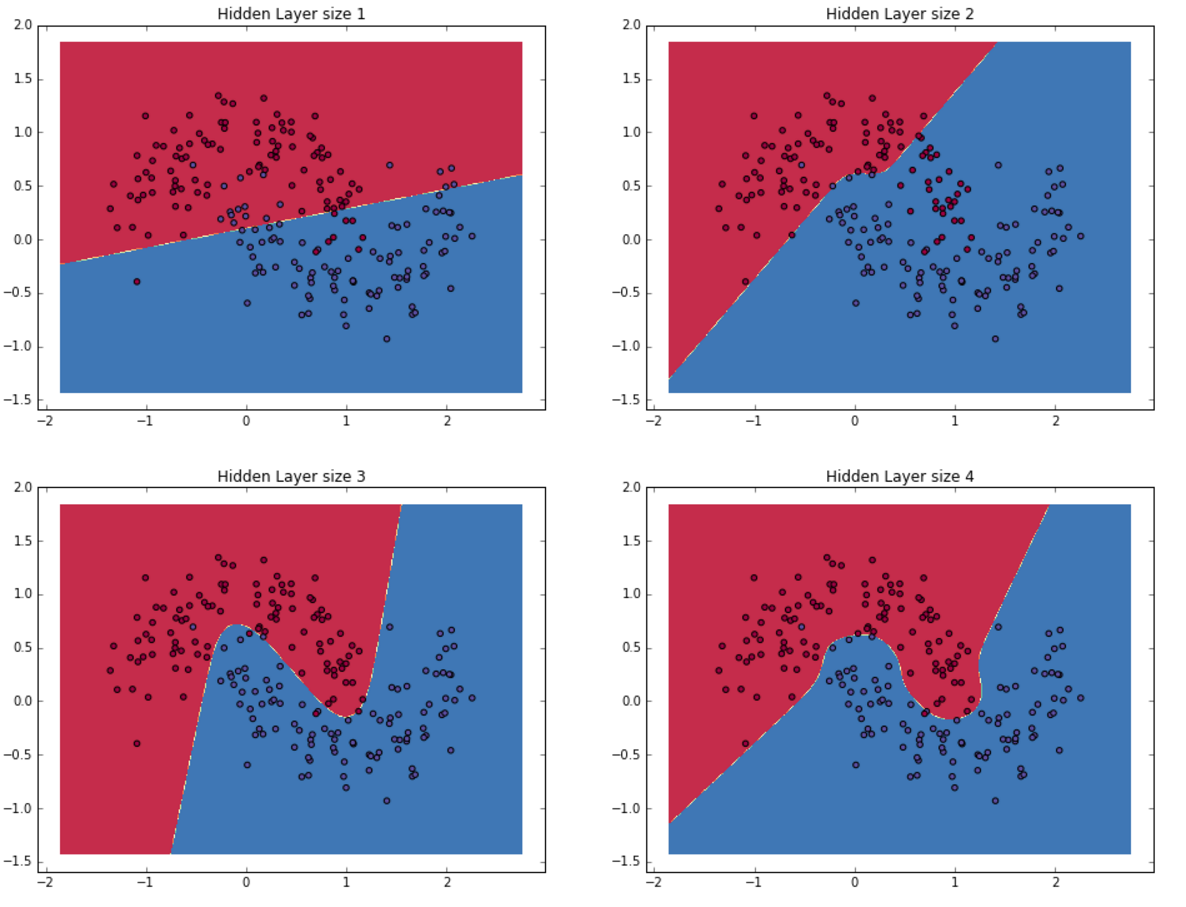
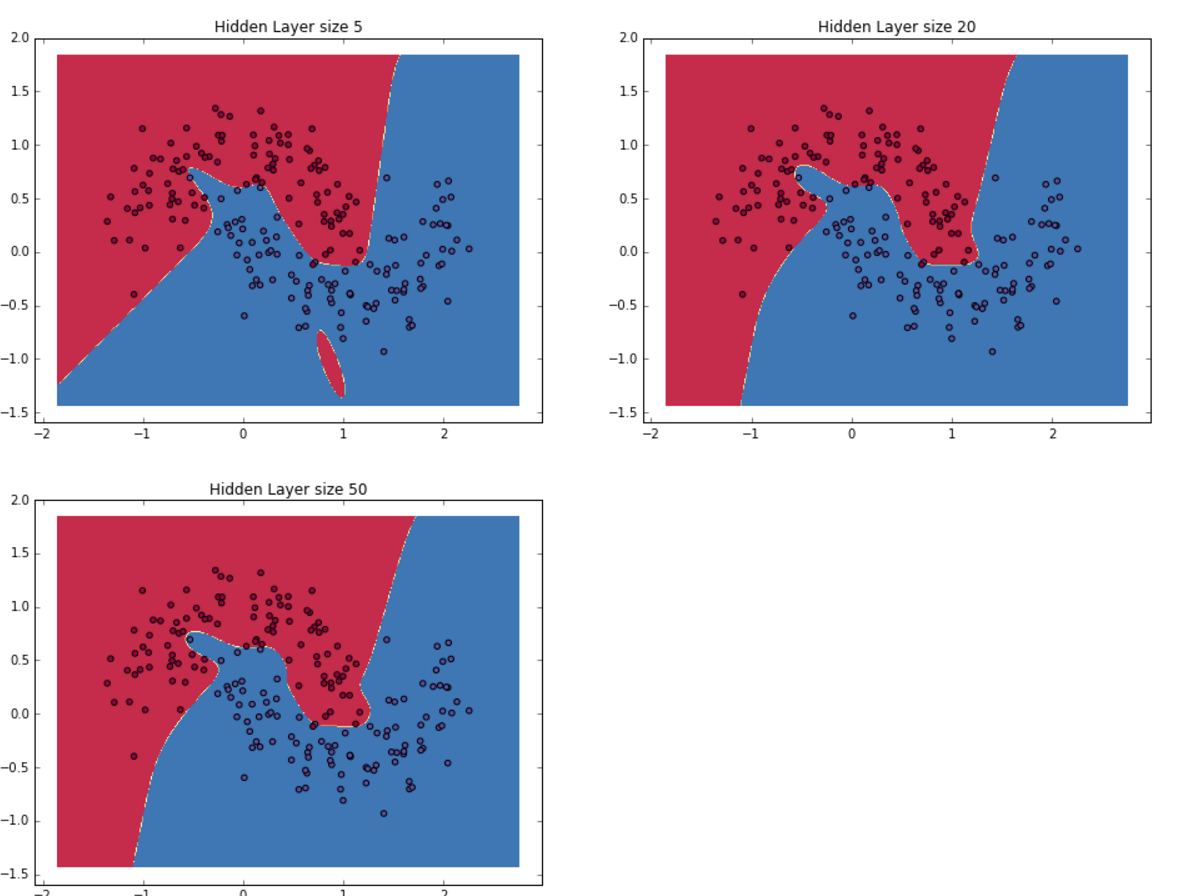
隐藏层神经元的数目越多,那么神经网络的复杂度就越高,需要的计算量就约到,但是其学习能力也就越强,当然过拟合的几率也就越大。至于隐藏层神经元的数目应该如何去选择,这个涉及模型选择相关的问题,这里并不讨论。
之前说了,神经网络中每个神经元都是一个感知机,对于感知机而言,最重要的就是其激活函数的选择。
这里可以这么理神经网络:每一个圆圈都代表一个激活函数,而每一条带箭头的线段都代表一次乘积,每个线段上都有一个权值;带箭头的线段的输入,是其输入端圆圈的输出,而带箭头线段的输出,是其输入和线段上的权值的乘积。每个圆圈的作用就是将输入到当前神经元的数据做一个求和,然后再对求和的结果使用激活函数,就可以得到神经元的输出。
各层激活函数的选择
对于输入层而言,可以认为输入层没有激活函数,输入层就是将输入的数据原原本本的放到了神经网络之中。
对于隐藏层而言,其激活函数的选择有很多,一般使用的是下面这三种函数:
函数
----------------------
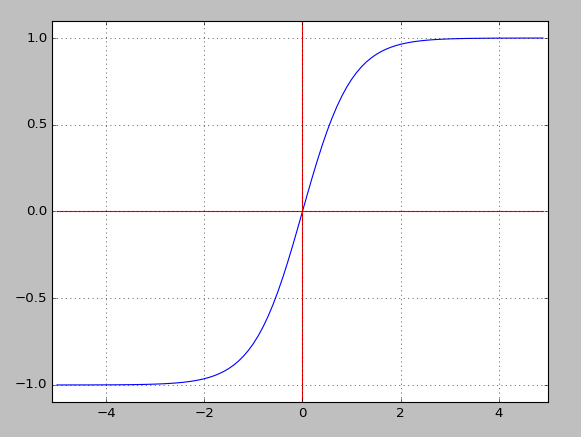
函数
----------------------
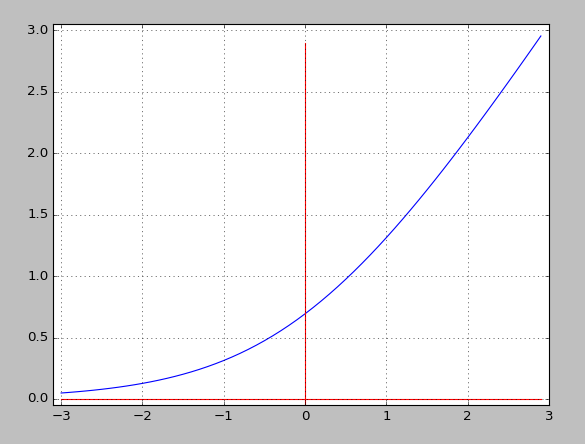
函数
函数导数是 函数
---------------------
上面这三个函数的共同特点就是,其求导十分的容易,使用自身的结果就可以得到导数。
这里仅仅考虑使用 函数做代码演示,主要也是因为这个函数在绝大多数场合都很适用。
对于输出层而言,由于需要判断输入的样本属于哪一个类别,所以一般考虑使用 函数, 这个函数在多分类 回归中提到过:对于有 个类别的分类算法而言,将其输出转换成对应的概率。
假设神经网络输出的类别有 个,即需要将输入到神经网络中的样本分类到这 中类别中的某一个去,假设输入样本x,在隐藏层的输出是向量 ,那么输入样本x输入第 类的概率为:
显然, 这里的 代表的是输出层第 个神经元的输入,即
这里 或者说是 其实也可以写成 ,代表的是输出层第 个神经元的输出。
代表的是输出层所有神经元输出的总和。
函数最明显的特点在于:它把每个神经元的输入占当前层所有神经元输入之和的比值,当作该神经元的输出。这使得输出更容易被解释:神经元的输出值越大,则该神经元对应的类别是真实类别的可能性更高。另外, 不仅把神经元输出构造成概率分布,而且还起到了归一化的作用,适用于很多需要进行归一化处理的分类问题。
的导数:
如果
如果
损失函数的选择
一般来说,基于 函数的神经网络,所使用的损失函数(Cost Function)是交叉熵损失函数(Cross-entropy cost function)。
平方损失函数
在之前机器学习的算法中,大部分算法所使用的的损失函数都是SSE,即平方误差和。但是SSE损失函数有一个比较大的缺点,就是这个损失函数在初始化权值和目标权值差的很远的时候,其收敛速度特别慢,只有在权值相对接近最优解的时候,收敛速度才比较的快,其测试代码和结果如下:
#-*- coding=utf-8 -*-"""@file : test_perceptron.py@author : duanxxnj@163.com@time : 2016-11-15"""import matplotlib.pyplot as pltimport numpy as npfrom dxxlearn.linear_model.perceptron import Perceptron# 这里使用单个感知机,单输入做为测试样本# 主要用于测试初始化权值对平方误差损失函数收敛速率的影响clf = Perceptron(300, 0.01)# 初始化权值为w=[2, 2]cost1 = clf.train(np.array([[1, 1]]), [0], clf.sigmoid, w_in=2)# 初始化权值为w=[0.6, 0.6]cost2 = clf.train(np.array([[1, 1]]), [0], clf.sigmoid, w_in=0.6)plt.plot(cost1, label='init w=[2, 2]', c='b')plt.plot(cost2, label='init w=[0.6, 0.6]', c='r')plt.legend()plt.grid()plt.show()
这里是不同的初始 对应的平方损失的收敛速度:
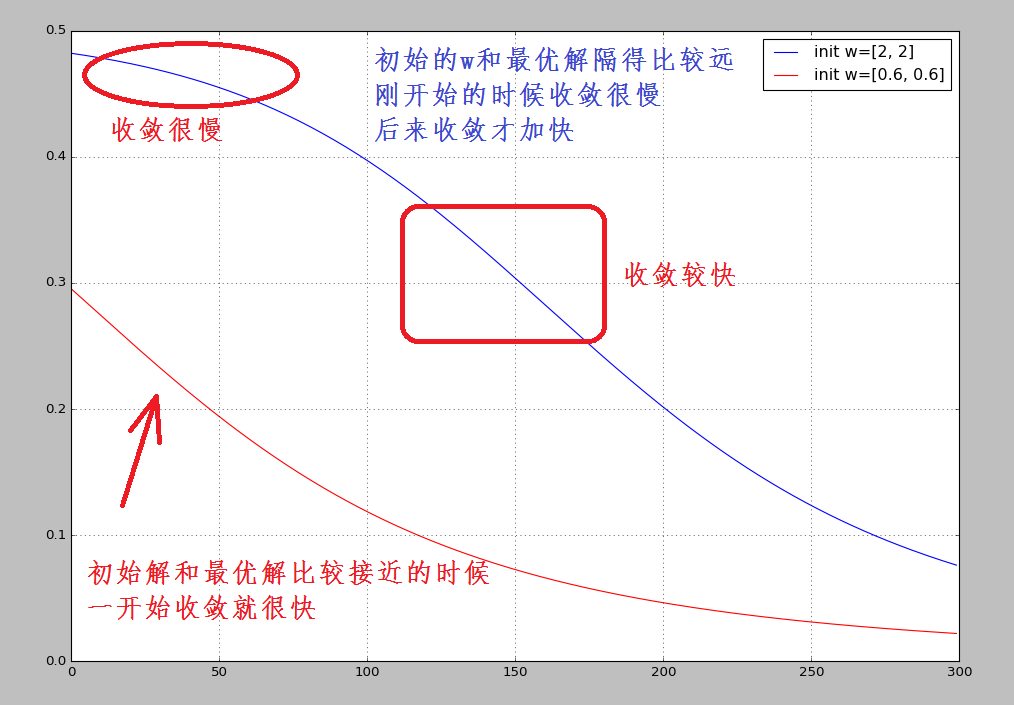
初始权值选择比较好的红色线,其代价随着训练次数增加而快速降低
初始权值选择不太好的蓝色线,其代价在一开始下降得非常缓慢,后来才加快收敛速度
直观上看,初始的误差越大,收敛得越缓慢。但是,根据我们自己的直观感觉,如果初值选择的不好,和最优解有很大的偏离,那么在一开始的时候,其收敛的速度应该是最快的才对。而不应该一开始收敛很慢。
其实,当初始权值选择偏离比较大的时候,收敛速度慢的主要原因在于使用的损失函数:
这里 取
那么,的导数为:
很显然,的导数中 和 可以认为是常数,因为这两个值可以直接从训练样本中计算出来,于是乎, 的导导数和 函数的导数成线性关系。
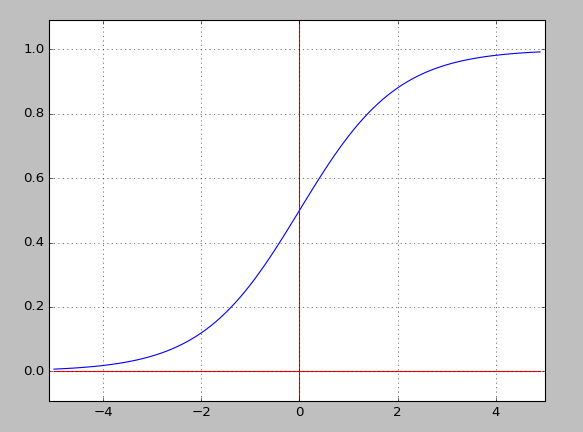
而 函数和其导数导数如下图所示,显然在刚开始的时候,收敛很慢,随和逐步增加收敛速度的。
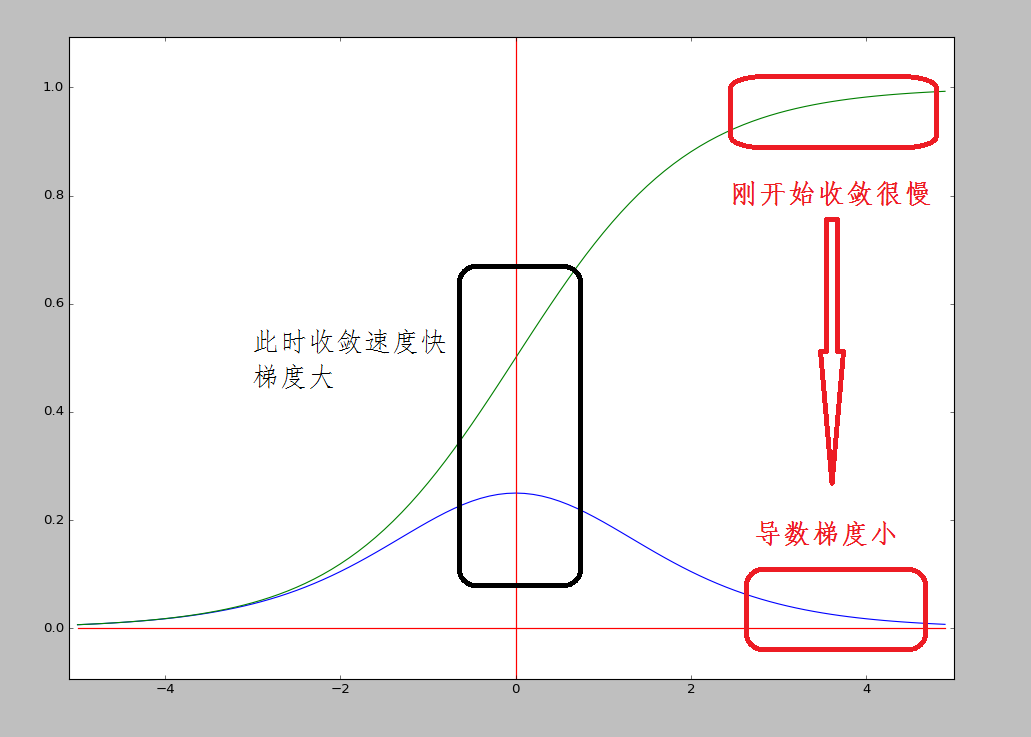
由于 函数的形式如此,所以,平方误差和损失函数的导数和 函数成线性关系,平方误差和损失函数的收敛在初始偏离很大到时候,收敛非常慢。这就是初始的代价(误差)越大,导致训练越慢的原因。
交叉熵损失函数
交叉熵与熵的关系,如同协方差与方差的关系一样,关于熵,会在其他的文章中详细说明,并不是本文的重点。
二分类交叉熵损失函数:
参数求解过程
基于上面所说的内容,这里将神经网络的参数求解过程概要性的推导一遍。
正向传播
当神经网络需要对样本进行预测的时候,使用的是正向传播算法。其实这个过程仅仅是一些矩阵和激活函数之间的乘法而已。这里假设:
1、 是一个 n 维的输入
2、总的样本个数为
3、是类别向量(对于三个类别而言,类别一:[1, 0, 0];类别二:[0, 1, 0];类别三:[0, 0, 1])
4、是输入经过神经网络之后预测得到的类别向量
5、隐藏层激活函数使用 函数(使用 函数也是一样的)
6、输出层激活函数使用 函数
7、损失函数使用交叉熵损失函数
8、第 层的输入为 ,第 层使用过激活函数后的输出为
9、 是第 层的参数
那么,对于只有一个隐藏层的神经网络而言,其参数分布如下:
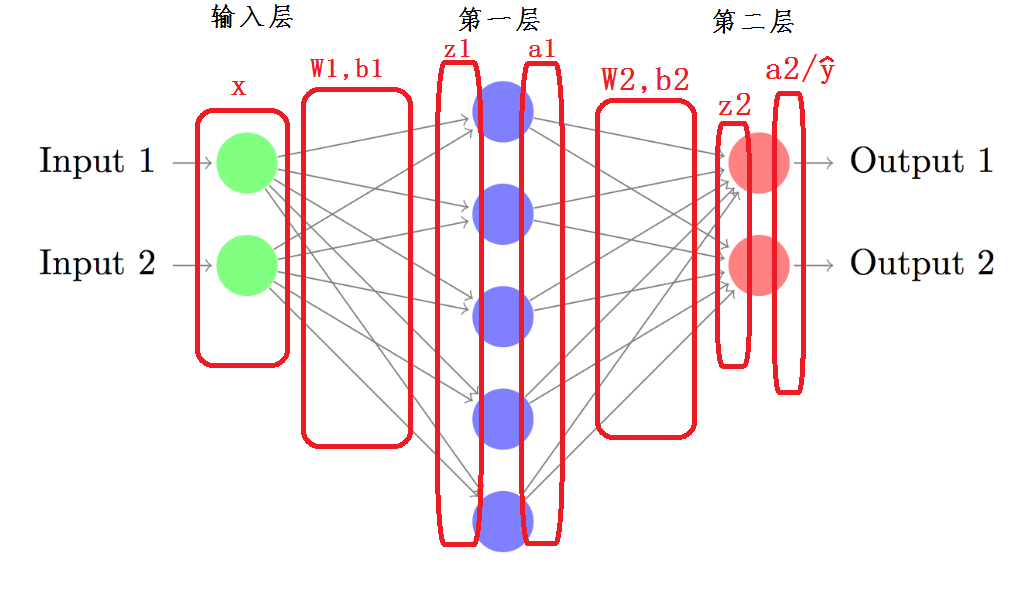
前向算法实现:
这里假设输入层有 个神经元,隐藏层有 个神经元,输出层有 个神经元,那么:
反向传播
损失函数是交叉熵损失函数(cross-entropy loss),也叫做negative log likelihood:
然后再对损失函数求导:
BP神经网络代码实现
#-*- coding=utf-8 -*-"""@file : nn_classfication_tests.py@author : duanxxnj@163.com@time : 2016/11/15 14:30"""import numpy as npfrom sklearn import datasets, linear_modelimport matplotlib.pyplot as pltclass Config:nn_input_dim = 2 # input layer dimensionalitynn_output_dim = 2 # output layer dimensionality# Gradient descent parameters (I picked these by hand)epsilon = 0.01 # learning rate for gradient descentreg_lambda = 0.01 # regularization strengthdef generate_data():np.random.seed(0)X, y = datasets.make_moons(200, noise=0.20)return X, ydef visualize(X, y, model):# plt.scatter(X[:, 0], X[:, 1], s=40, c=y, cmap=plt.cm.Spectral)# plt.show()plot_decision_boundary(lambda x:predict(model,x), X, y)plt.title("Logistic Regression")def plot_decision_boundary(pred_func, X, y):# Set min and max values and give it some paddingx_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5h = 0.01# Generate a grid of points with distance h between themxx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))# Predict the function value for the whole gidZ = pred_func(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)# Plot the contour and training examplesplt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)plt.show()# Helper function to evaluate the total loss on the datasetdef calculate_loss(model, X, y):num_examples = len(X) # training set sizeW1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']# Forward propagation to calculate our predictionsz1 = X.dot(W1) + b1a1 = np.tanh(z1)z2 = a1.dot(W2) + b2exp_scores = np.exp(z2)probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)# Calculating the losscorect_logprobs = -np.log(probs[range(num_examples), y])data_loss = np.sum(corect_logprobs)# Add regulatization term to loss (optional)data_loss += Config.reg_lambda / 2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)))return 1. / num_examples * data_lossdef predict(model, x):W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']# Forward propagationz1 = x.dot(W1) + b1a1 = np.tanh(z1)z2 = a1.dot(W2) + b2exp_scores = np.exp(z2)probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)return np.argmax(probs, axis=1)# This function learns parameters for the neural network and returns the model.# - nn_hdim: Number of nodes in the hidden layer# - num_passes: Number of passes through the training data for gradient descent# - print_loss: If True, print the loss every 1000 iterationsdef build_model(X, y, nn_hdim, num_passes=20000, print_loss=False):# Initialize the parameters to random values. We need to learn these.num_examples = len(X)np.random.seed(0)W1 = np.random.randn(Config.nn_input_dim, nn_hdim) / np.sqrt(Config.nn_input_dim)b1 = np.zeros((1, nn_hdim))W2 = np.random.randn(nn_hdim, Config.nn_output_dim) / np.sqrt(nn_hdim)b2 = np.zeros((1, Config.nn_output_dim))# This is what we return at the endmodel = {}# Gradient descent. For each batch...for i in range(0, num_passes):# Forward propagationz1 = X.dot(W1) + b1a1 = np.tanh(z1)z2 = a1.dot(W2) + b2exp_scores = np.exp(z2)probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)# Backpropagationdelta3 = probsdelta3[range(num_examples), y] -= 1dW2 = (a1.T).dot(delta3)db2 = np.sum(delta3, axis=0, keepdims=True)delta2 = delta3.dot(W2.T) * (1 - np.power(a1, 2))dW1 = np.dot(X.T, delta2)db1 = np.sum(delta2, axis=0)# Add regularization terms (b1 and b2 don't have regularization terms)dW2 += Config.reg_lambda * W2dW1 += Config.reg_lambda * W1# Gradient descent parameter updateW1 += -Config.epsilon * dW1b1 += -Config.epsilon * db1W2 += -Config.epsilon * dW2b2 += -Config.epsilon * db2# Assign new parameters to the modelmodel = {'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}# Optionally print the loss.# This is expensive because it uses the whole dataset, so we don't want to do it too often.if print_loss and i % 1000 == 0:print("Loss after iteration %i: %f" % (i, calculate_loss(model, X, y)))return modeldef classify(X, y):# clf = linear_model.LogisticRegressionCV()# clf.fit(X, y)# return clfpassdef main():X, y = generate_data()model = build_model(X, y, 3, print_loss=True)visualize(X, y, model)if __name__ == "__main__":main()
这里有一点需要说明,就是隐藏层的神经元的个数基本上代表的是该神经网络的复杂度。复杂度越高,神经网络的分类能力越强,同时其过拟合的可能性也就越大: