题解(bitset版）

part.1 什么是格雷码

格雷码（Gray Code）是一种特殊的二进制编码方式，其核心特性在于：任意两个相邻的数之间仅有一位二进制位不同。这种特性使得格雷码在许多工程和算法问题中具有广泛应用，例如减少数字转换过程中的出错概率、优化状态转移等。

part.2 二进制转格雷码

我们可以用一种“列竖式”的方式将二进制转化为格雷码

需要的知识点-异或&二进制

我们以3（二进制为0011为例）

首先，列一个竖式

方法：

步骤一：将相同的数字下移然后向右移$1$位，进行异或运算

如图所示

附件-异或：

异或是在各种计算机语言中，如C、C++、java等，使用按位异或的思想执行的操作。异或逻辑的关系是：当AB不同时，输出$P=1$；当AB相同时，输出$P=0$。“⊕”是异或数学运算符号

步骤二：进行按位异或运算

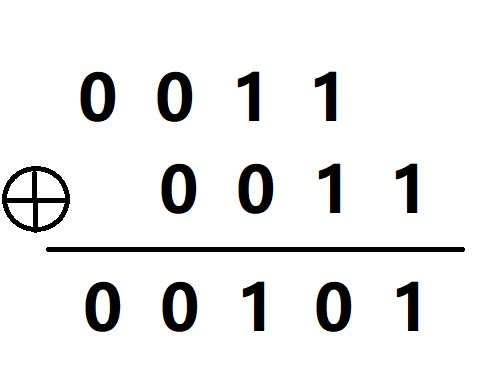
解释：

1.第一位只有一个$0$，抄下来
2.第二位两个$0$，相同，故为零
3.第三位一个$1$一个$0$,不同，故为一
4.第四位两个$1$，相同，故为零
5.第五位只有一个$1$，抄下来
6.故答案为$00101$

步骤三：去掉最后一位

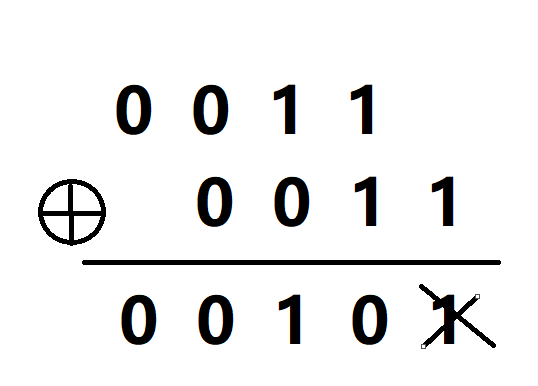
故3的格雷码为0010

part.3 题目解读

题目原文

P5657 [CSP-S2019] 格雷码

题目描述

通常，人们习惯将所有 $n$ 位二进制串按照字典序排列，例如所有 2 位二进制串按字典序从小到大排列为：00，01，10，11。

格雷码（Gray Code）是一种特殊的 $n$ 位二进制串排列法，它要求相邻的两个二进制串间恰好有一位不同，特别地，第一个串与最后一个串也算作相邻。

所有 2 位二进制串按格雷码排列的一个例子为：00，01，11，10。

$n$ 位格雷码不止一种，下面给出其中一种格雷码的生成算法：
1. 1 位格雷码由两个 1 位二进制串组成，顺序为：0，1。
2. $n + 1$ 位格雷码的前 $2^n$ 个二进制串，可以由依此算法生成的 $n$ 位格雷码（总共 $2^n$ 个 $n$ 位二进制串）按顺序排列，再在每个串前加一个前缀 0 构成。
3. $n + 1$ 位格雷码的后 $2^n$ 个二进制串，可以由依此算法生成的 $n$ 位格雷码（总共 $2^n$ 个 $n$ 位二进制串）按逆序排列，再在每个串前加一个前缀 1 构成。

综上，$n + 1$ 位格雷码，由 $n$ 位格雷码的 $2^n$ 个二进制串按顺序排列再加前缀 0，和按逆序排列再加前缀 1 构成，共 $2^{n+1}$ 个二进制串。另外，对于 $n$ 位格雷码中的 $2^n$ 个 二进制串，我们按上述算法得到的排列顺序将它们从 $0 \sim 2^n - 1$ 编号。

按该算法，2 位格雷码可以这样推出：

1. 已知 1 位格雷码为 0，1。
2. 前两个格雷码为 00，01。后两个格雷码为 11，10。合并得到 00，01，11，10，编号依次为 0 ~ 3。

同理，3 位格雷码可以这样推出：

1. 已知 2 位格雷码为：00，01，11，10。
2. 前四个格雷码为：000，001，011，010。后四个格雷码为：110，111，101，100。合并得到：000，001，011，010，110，111，101，100，编号依次为 0 ~ 7。

现在给出 $n$，$k$，请你求出按上述算法生成的 $n$ 位格雷码中的 $k$ 号二进制串。

输入格式

仅一行两个整数 $n$，$k$，意义见题目描述。

输出格式

仅一行一个 $n$ 位二进制串表示答案。

。

【数据范围】

对于 $50\%$ 的数据：$n \leq 10$

对于 $80\%$ 的数据：$k \leq 5 \times 10^6$

对于 $95\%$ 的数据：$k \leq 2^{63} - 1$

对于 $100\%$ 的数据：$1 \leq n \leq 64$, $0 \leq k \lt 2^n$

简化：n代表格雷码的位数，k代表格雷码的十进制，就是把k化成n位的格雷码

part.4 题目思路

1.将k转化为二进制

可以使用bitset
不会bitset点此了解

string b=bitset<64>(k).to_string();

意思：将k转化为64位的二进制，并且用s存起来

2.将s转化为n位

因为bitset中的位数只支持常数，所以我们只能声明初始为数据范围的最大值（64位）

所以我们要保留s的后n位，可以使用函数substr

b=b.substr(64 - n);

3.将二进制转化为格雷码

参考上文，递推式为

代码

#include<bits/stdc++.h>
using namespace std;
int main() {
   unsigned long long n,k;
   cin>>n>>k;
   string b=bitset<64>(k).to_string(),gray;
   b=b.substr(64 - n);
   gray+=b[0]; 
   for(int i=1;i<n;i++) gray+=(b[i]==b[i-1])?'0':'1';
   cout<<gray;
   return 0;
}