@l1ll5 2020-02-11T04:00:12.000000Z 字数 12657 阅读 2587

基础数据结构杂谈

—— by 东北师范大学附属中学 l1ll5

写在前面的话

由于划定的讲课范围比较坑爹，从单调栈划到了树套树，难度跨度很大。
因为我写这篇课件的时候基本还没有见过大家，所以基于世除我佬，猜想大家都很强，太水的东西就略讲啦。
准备的内容貌似有点多...大家视情况可以随时要求调整速度。
佬.jpg-47.1kB
你可以通过在BZOJ搜索l1ll5这个名字来找到我。

如果你们在前几天考了遥遥三十八万公里的航程和不可能的弹幕结界这两道题的话，它们是我出的。
如果你们还没考过的话，可能未来会考，都是很水的送分题~

宣一下个人博客，这里面可以找到下文提到的所有例题的题解和代码。

Q&A

Q：你是哪个菜？我怎么没听说过你。
A：我的确是个菜... 哭.png-1.8kB 所以没法掏出一堆很屌的个人成就来让你认识我...
Q：如果我事后发现了文章的错误想骂你该怎么办？
A：你可以加 QQ：2817629709 去骂我，或者在我的博客下留言。
Q：如果我现在就发现了文章的错误想骂你该怎么办？
A：那你就赶快拍桌子大喊 異議あり骂我吧~
Q：你讲的东西太水我想睡觉怎么办？
A：请睡吧...
Q：你讲的东西太神我听不懂怎么办？
A：那你一定是在假...

难度差别较大，大家可以选认为可以听一听的东西选听。
讲的顺序是：单调栈->树状数组->线段树->主席树->树套树->K-Dtree
~~方便大家遇到想听的东西后及时醒来~~

数据结构

data structure
和算法并列的，OI的重要组成部分。
与大多数常见题目不同，数据结构题目大部分拥有相对较小的，不依赖于灵光一现的思维难度，所以可能做不来思维题的同学会比较喜欢做数据结构题。
今天选讲其中最基础的一部分...

单调栈

地球人都会的东西。
为什么要把它和单调队列分开呢？

栈

一个栈是一个垃圾桶，后丢进去的东西在栈顶，先丢进去的东西在栈底，只能从栈顶往外拿东西。
可以发现，我们在递归的过程中实际上就是维护了一个栈，每次处理栈顶。

单调栈

这个栈中的元素具有自底向上的单调递增/单调递减性。
由于栈中元素是有序的，可以根据这个性质解决一些问题。

例 $1$

题意：给一个序列，求序列中每个元素和它右边第一个比它大的元素的距离的和。
（可能和原题意不完全一致，在此不考虑等于的边界情况。）

题解：非常经典的题，设数组 $nxt_i$ 表示 $i$ 右边第一个比它大的数的位置。 $nxt$ 数组很多时候都能用到。

我们自左向右的考虑每个元素，维护一个单调递减的栈。
为什么要单调递减呢，考虑什么时候一个新进的元素可以更新旧元素的答案。

该旧元素没被更新过。
该旧元素小于新进元素。

考虑如果有一些元素是自左向右单调递减的，则如果新进元素可以更新最后一个元素的答案，也可以更新之前元素的答案直至不能更新为止。
暴力更新的复杂度是 $O(n^2)$ 的，不能接受。所以可以用一个数据结构去优化这个过程，考虑到一个元素只会被更新一次，即被它右边最近的符合要求的元素更新，则限定这个数据结构的元素只能进出各一次。
考虑到需要快速找到新进元素可以更新哪些旧元素，则令这个数据结构的元素具有自左向右的单调递减性。
这样的话，如果新进元素可以更新一个旧元素，就这样更新到不能更新位置，然后将这个元素丢入单调栈即可。
由于每个元素只会进出一次，时间复杂度为 $O(n)$ 。
BZOJ 1660 乱发节

关于 $nxt$ 数组的一个常用性质：随机序列的情况下， $nxt_i-i$ 的期望值是 $log_n$ 的。
~~可以用来骗分~~

就讲这点好了。

树状数组

( Binary Indexed Tree )
常简写为 $bit$

挺好玩但是可（被）替代性很强的一个精巧的小数据结构。

考虑这样一个问题：
给定一个长为 $n$ 的序列 $A$ ，有 $m$ 次操作。

$add$ $x$ $y$ ：令 $a_x=a_x+y$
$ask$ $l$ $r$ ：查询 $sum_{i=l}^{r} a_i$

$n,m \leq 10^6$

考虑一个差分思想，记 $sum_i$ 表示从 $1$ 到 $i$ 的前缀和，显然对于查询操作有 $ans=sum_r-sum_{l-1}$ 。
虽然查询操作是 $O(1)$ 的，但是对于修改操作，暴力的话每次要修改 $O(n)$ 个 $sum$ ，考虑优化掉这个过程。
换一种方法高效的平衡复杂度。

构造数组 $c$ ，对于 $c$ 有：

$c_1=a_1$
$c_2=a_1+a_2$
$c_3=a_3$
$c_4=a_1+a_2+a_3+a_4$
$c_5=a_5$
$c_6=a_5+a_6$
$c_7=a_7$
$c_8=a_1+a_2+...+a_8$
$...$
$c_{16}=a_1+a_2+...+a_{16}$

形式话的说，定义 $lowbit_i$ 为 $i$ 在二进制下的低位起第一个 $1$ ，则有 $c_x=sum_{i=x-lowbit_x+1}^{x} a_i$
即 $c_i$ 维护了 $(x-lowbit_x,x]$ 这个区间的信息。

那么考虑怎么实现查询操作：

int ask(int x)
{
    int ret=0;
    for(;x;x-=lowbit(x))
    ret+=c[x];
    return ret;
}

这个操作实现了一次从 $1$ 到 $x$ 的前缀和查询，没什么好说的吧？
用 $c$ 数组拆分了区间，每次将这些区间的贡献累加起来。
记 $\Delta x=x-lowbit(x)$ ，则首先累计 $(\Delta x,x]$ 的答案，再考虑 $(\Delta x-lowbit_{\Delta x},\Delta x]$ 的答案...以此类推。
正确性显然，由于每次消掉了 $x$ 二进制位下的一个 $1$ ，所以记 $bitcount_x$ 为 $x$ 在二进制下 $1$ 的个数，则单次询问的复杂度是 $O(bitcount_n)$ 的，上界为 $O(log_n)$ ，常数非常小，而且是非递归实现。

对于对 $a_x$ 的修改操作，只要找到有哪些 $c_i$ 包含了 $a_x$ ，直接更新它们的答案即可。
先看代码：

void add(int x,int v)
{
    for(;x<=n;x+=lowbit(x))
    c[x]+=v;
}

不压行的两行代码，可以说是非常的优美简洁了
为什么这么做是正确的呢？
我们根据 $lowbit_x$ 的不同取值为 $x$ 分组，显然 $x$ 只有不同的 $log_n$ 组。
存在这样的一个性质：对于每组不同的 $lowbit_x$ ，最多存在一个位置可以覆盖 $x$ 。
证明是不困难的：
考虑这样的一个 $k$ 包含了 $x$ ：
即 $k-lowbit_k < x \leq k$
则 $k$ 和 $x$ 的二进制组成一定是形如这样的：
$k:X10000$
$x:X01000$
其中 $X$ 是相同的两部分。
为什么呢？如果 $X_k$ 更大，显然减去 $lowbit_k$ 后还是比 $x$ 大。
如果 $X_k$ 较小，则本来就比 $x$ 小了，都不成立，所以必然是相同的两部分。
我们称呼 $X$ 后的第一个 $1$ 为关键位。则 $k$ 的关键位后必须均为 $0$ ，否则不满足在同一个 $lowbit$ 组内。
现在考虑存在另一个数 $p$ 也在同一个 $lowbit$ 组内包含了 $x$ ，则 $p$ 的二进制组成如下：
$p：Y1Z$
考虑关键位后的 $Z$ ，一定全为 $0$ 。
考虑关键位前的 $Y$ ，一定与 $X$ 相同。
所以不存在这样一个合法的 $p$ 。
这样的话，显然每次 $+=lowbit_i$ 的操作都消掉了目前的最低位，进入了一个新的 $lowbit$ 组。
不重不漏的遍历了所有包含 $x$ 的区间。

这个图可以直观的感受树状数组。
此处输入图片的描述

方便好写
常数很小，实际运行速度飞快
不能解决大多数问题

一个比较常见的小技巧：树状数组维护区间加和区间求和。

我们知道树状数组维护的是前缀信息，可以利用差分的思想解决解决区间修改单点询问和单点修改区间询问这两个问题。但是对于区间询问和区间修改看起来就无能为力了。
实际不然。
依旧考虑差分的思想，记 $det_i$ 为下标为 $i$ 的数的目前改变量，考虑如下式子：
$sum_i = \sum_{j=1}^{i} a_j + det_1 \times i+det_2\times (i-1) + ... +det_i\times 1$
$sum_i = \sum_{j=1}^{i} a_j + \sum_{j=1}^{i}det_j\times (i-j+1)$
$sum_i = \sum_{j=1}^{i} a_j + (i+1) \sum_{j=1}^{i}det_j - \sum_{j=1}^{i}det_j\times j$

分别维护 $det_i$ 和 $det_i \times i$ 的前缀和即可，跑的飞起。
在用于辅助高级数据结构的时候很方便~
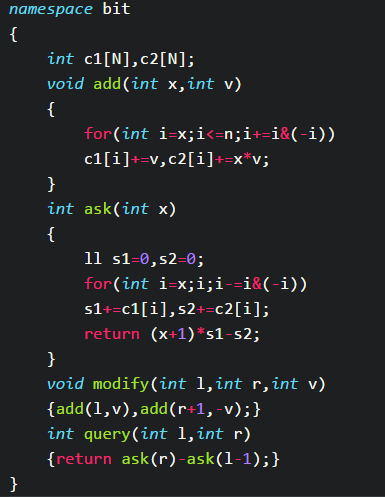
bit.png-35.1kB

geili.jpg-3.5kB

这个思想可以推广到更高维的情况，二维树状数组也可以这样简单的差分统计。
具体式子有点长，不写了，感兴趣可以自己画一画，超休闲的~

例 $1$

题意：平面内有 $n$ 棵树， $m$ 次询问，每次询问一个矩形内有多少棵树。
$n,m \leq 5 \times 10^5 , 0 \leq x_i,y_i \leq 10^9$
允许离线。

无语.jpg-4kB

题解：
发现坐标范围很大，可以离散化。
离线所有询问，由于树状数组只能维护前缀信息，将一个询问拆成四个询问。（容斥）
考虑我们可以简单的维护一列的信息，进一步，可以维护这一列和所有处理过的列的信息和。
那么按照 $x$ 为关键字排序所有询问，每次就可以直接累计之前处理过的信息了。
对于 $y$ 的限制，直接树状数组维护，时间复杂度 $O(nlog_n)$

思想：离线操作序列，对于二维限制通常排序一维和用数据结构维护另一维。
BZOJ 1935 [Shoi2007]Tree 园丁的烦恼

例 $2$

题意：给一个序列，多次查询区间有多少个数出现了两次及以上。
$n,m,a_i \leq 10^6$
允许离线

原题的话用莫队算法可以随便 $O(n \sqrt n )$ 的过， BZOJ 上加强了数据，要求优越的 $O(nlog_n)$ 做法。
显然是钦定树状数组了。

无语.jpg-4kB

题解：
处理出下标为 $i$ 的数下一次出现的位置 $nxt_i$ 。
显然第一次出现一个数是对答案没有贡献的，但是第二次以后就都有了。
也就是说，如果我们保证这个数第一次出现了，就可以在第二次出现的地方 $+1$ ，直接统计区间和即可，因为如果接下来出现是没有影响的。
这样的话如果所有询问区间的左端点都为 $1$ 就可以做了，但是不是，怎么办呢？
离线所有询问，将询问左端点从左往右移动。
每次移动都相当于在集合里删除了一个数，即不保证它的“第一次”是一定出现的了。
怎么办？将第二次赋为第一次，在第三次出现的地方统计答案即可，借助 $nxt$ 数组可以完成
时间复杂度 $O(nlog_n)$ 。

BZOJ 2743 [HEOI2012] 采花

可以体现树状数组必须性的题很少...就这样了。

线段树

这个比较重要所以讲的多一点：
由于难度波动较大大家也可以选听...

从零开始的线段树速成

普通线段树：

又是这个问题：
给定一个长为 $n$ 的序列 $A$ ，有 $m$ 次操作。

$add$ $x$ $y$ ：令 $a_x=a_x+y$
$ask$ $l$ $r$ ：查询 $sum_{i=l}^{r} a_i$

$n,m \leq 2\times 10^5$

就是不想用树状数组。

我们考虑一种类似分治的思想，我们可以把整个序列划分成多个段，处理出每个段的答案，每次查询操作如果包含了一个完整的段就把这个段的答案都加进去。~~如果到此为止这个算法就是分块...~~
然后，对每个分出的小段也继续这样的操作，直到我们分出不能再分的小段为止。

这个段应该怎么划分呢？显然这是一个大段（整个序列）包含了若干小段，而若干小段又划分成了更多小段。
常见的，也是比较优越的做法是每次二分目前序列，举个例子：
假设给出的序列长度 $n$ 为 $2048$ ，我们就可以将整个序列划分为 $[1,1024],[1025,2045]$ ，然后进一步的划分为 $[1,512],[513,1024],[1025,1536],[1537,2048]$ 。这样以此类推，直到划分的区间长度为 $1$ 为止。

此时考虑如果我们需要查询从 $1$ 到 $1088$ 的区间和 $S(l,r)$ ，发现 $S(1,1088)=S(1,1024)$ + $S(1025,1088)$
我们已经预处理出了 $S(1,1024)$ 的答案，直接加进去，这样一下子将答案的范围缩小了很多，继续划分 $S(1025,1088)$ 即可。

这就是线段树。
pttree

为什么说是线段“树”呢，因为这个数据结构考虑出来是一棵二叉树的形式，即父亲节点维护区间 $[l,r]$ ，父亲节点有左右两个儿子，分别维护区间 $[l,mid],[mid+1,r]$ 的信息，每次查询一个长度为 $1$ 的区间的操作实质上是在二叉树上的一次遍历，由根节点走到一个叶子节点。

对于修改操作，直接找到这个点被多少个区间所包含了，修改这些区间维护的区间和即可。

呃，复杂度呢？
比较容易分析的是修改操作，发现一次操作访问到的节点是树上的一条链，显然长度是 $O(log_n)$ 的。
对于查询操作，我们需要知道的是这次查询访问了多少个节点，发现一个事实是线段树上每次区间查询操作，每层最多只会访问到四个节点。
这是为什么呢？考虑我们目前访问的节点包括节点 $x$ ，则对于下一层需要访问的节点，如果 $x$ 的儿子都需要被完全访问，则根本不需要访问它们，考虑到单次查询的区间是连续的，为了单次访问到尽可能多的节点我们只能完全访问其中一个节点同时部分访问另一个节点，这样的话这个区间才有可能在这层的另一个节点处有覆盖。虽然这样访问了下一层的两个节点，但是同层我们只能再有一个节点可以访问下去了，因为完整跨过的区间都是不需要向下访问的，而另外的那个节点也只能向下访问两个节点，所以一层内最多访问四个节点。（看文字可能有点晕...自己 YY 下还是比较显然的）
故线段树区间操作的复杂度为 $O(log_n)$ 。

推论：一个区间在线段树上最多被分解成 $O(log_n)$ 个子区间。

但是由于是递归实现的和分析过程中就能看出来的原因，常数较大，实测比树状数组慢很多。

在实际的实现中，通常将线段建成一棵满二叉树，这样我们发现节点 $x$ 的左右儿子分别为 $2x$ 和 $2x+1$ 。

文艺线段树：

我们常常会遇到这样的问题：
给定一个长为 $n$ 的序列 $A$ ，有 $m$ 次操作。

$add$ $l$ $r$ $y$ ：令对于所有 $x \in [l,r]$ ， $a_x=a_x+y$
$ask$ $l$ $r$ ：查询 $sum_{i=l}^{r} a_i$

$n,m \leq 2\times 10^5$
虽然我们知道树状数组还是可以做但是我们还是不想做...

区间修改需要我们快速考虑修改操作带来的贡献，但是每次修改影响的区间是 $O(n^2)$ 的，没法搞。
不过我们知道：

一个区间在线段树上最多被分解成 $O(log_n)$ 个子区间。

利用这个性质，提出“懒”标记思想。
简而言之，就是每次在母区间打标记，意为我们修改了这个区间，但是暂时不考虑对子区间的影响。
当我们再次访问到这个区间，并不得不访问它的子区间的时候，再考虑这个修改标记对子区间的影响。
显然复杂度仍然为 $O(log_n)$

线段树几乎是除了数组和栈的数据结构中最最最常用的了，为什么？
我们刚刚考虑的是区间加和区间求和，这个标记很简单，也很好处理。
线段树可以处理几乎所有标记信息，只要这个信息满足：

修改可下传性，即可快速计算修改操作对子区间的影响。
查询可上传性，即可快速用子区间的信息修改母区间的信息。

举个简单的例子：
区间赋值，对母区间赋值即一定对子区间进行了一样的赋值，这个修改操作可以简单下传。
区间最值，母区间的最值一定是通过子区间的最值取最值转移而来的，这个询问操作可以简单上传。
举几个稍复杂点的例子：

例 $1$

题意：单点修改，查询区间最大连续子段和。
$n \leq 5 \times 10^5 , m \leq 10^5$
不要求在线，有在线做法。

无语.jpg-4kB

题解：
发现最大连续子段和具有可上传性，对于一个区间，要么全选，要么选左起的一段，要么选右起的一段。
分别维护这三个信息即可。
上传的时候分三种情况讨论。

左全选，右选左起
右全选，左选右起
左右全选

修改操作直接找到叶子修改，一路上传上来即可。
时间复杂度 $O(nlog_n)$

BZOJ 1756 Vijos1083 小白逛公园　

例 $2$

题意：
区间两种修改：将小于一个数的数都变成这个数，将大于一个数的数都变成这个数。
最后查询整个序列。
数据范围可以认为是要求 $O(nlog_n)$ 做法。
不要求在线，有在线做法。

无语.jpg-4kB

题解：
朴素的考虑，修改操作实质上修改了区间最值，那么直接维护区间最值就行了。对于修改操作带个区间赋值标记，最后输出所有叶子节点的最值。
上下传都是简单的。
仔细一想可以发现，其实区间最值是什么根本不需要维护，直接维护区间覆盖标记即可，因为覆盖标记已经可以维护这个信息了，这样的话不需要上传标记，只需要下传。
为什么？显然父亲节点的信息更加新啊。这样写比之前的写法快了一倍。

QQ截图20171224190826.png-15.7kB

BZOJ 4364 [IOI2014]wall砖墙

例 $3$

题意：给一个 $01$ 序列，支持区间赋值，区间取反，查询区间和，查询区间最长连续 $1$

这题其实题意即题解，但是需要维护的信息很多，很适合用来练习对线段树多标记上下传的处理问题...
请大家说一说都需要维护哪些信息？

无语.jpg-4kB

我的写法是多少这样的：

分别维护区间最多连续 0/1，区间左右连续 0/1，区间覆盖标记，区间和，区间取反标记

最好先拿一张纸写下来各种标记和转移方式。
上下传的时候注意细节...

int len[N<<2][2],L[N<<2][2],R[N<<2][2],cov[N<<2];//最多连续01 左右连续01 覆盖
int sum[N<<2],rev[N<<2];//求和 取反
void pushup(int x,int l,int r)
{
    int ls=x<<1,rs=x<<1|1;
    int mid=(l+r)>>1;
    sum[x]=sum[ls]+sum[rs];
    len[x][0]=Mx(len[ls][0],len[rs][0]);
    len[x][0]=Mx(len[x][0],R[ls][0]+L[rs][0]);
    len[x][1]=Mx(len[ls][1],len[rs][1]);
    len[x][1]=Mx(len[x][1],R[ls][1]+L[rs][1]);
    L[x][0]=L[ls][0]+(L[ls][0]==mid-l+1)*L[rs][0];
    L[x][1]=L[ls][1]+(L[ls][1]==mid-l+1)*L[rs][1];
    R[x][0]=R[rs][0]+(R[rs][0]==r-mid)*R[ls][0];
    R[x][1]=R[rs][1]+(R[rs][1]==r-mid)*R[ls][1];
}
void pushdown(int x,int l,int r)
{
    int ls=x<<1,rs=x<<1|1;
    int mid=(l+r)>>1;
    if(cov[x]!=-1)
    {
        if(cov[x]==0)
        {
            rev[ls]=rev[rs]=0;
            sum[ls]=sum[rs]=0;
            cov[ls]=cov[rs]=0;
            len[ls][1]=len[rs][1]=L[ls][1]=L[rs][1]=R[ls][1]=R[rs][1]=0;
            len[ls][0]=R[ls][0]=L[ls][0]=mid-l+1;
            len[rs][0]=R[rs][0]=L[rs][0]=r-mid;
        }
        else
        {
            rev[ls]=rev[rs]=0;
            len[ls][1]=L[ls][1]=R[ls][1]=sum[ls]=mid-l+1;
            len[rs][1]=L[rs][1]=R[rs][1]=sum[rs]=r-mid;
            cov[ls]=cov[rs]=1;
            len[ls][0]=len[rs][0]=L[ls][0]=L[rs][0]=R[ls][0]=R[rs][0]=0;
        }
    }
    if(rev[x])
    {
        rev[ls]^=1,rev[rs]^=1;
        sum[ls]=mid-l+1-sum[ls];
        sum[rs]=r-mid-sum[rs];
        swap(len[ls][0],len[ls][1]);
        swap(len[rs][0],len[rs][1]);
        swap(L[ls][0],L[ls][1]);
        swap(L[rs][0],L[rs][1]);
        swap(R[ls][0],R[ls][1]);
        swap(R[rs][0],R[rs][1]);
    }
    rev[x]=0;cov[x]=-1;
}

嗯...我写的可能不太优雅。
BZOJ 1858 [Scoi2010] 序列操作

上面几个题可以帮助大家更好的理解打标记的相关思想，其中最后一题更可以提升代码能力...

下面说一个线段树实现中的小技巧：

例 $4$

题意：对于一个下标为 $1 - 10^9$ 的数列， $n$ 次操作，将区间 $[a,b)$ 这个区间中所有比 $k$ 小的数改为 $k$ ，求最终数列和。

这个操作实际上是维护区间最值，没什么特殊的，重点是发现这个序列的长度非常长，直接开肯定是空间双爆炸的...
怎么办呢？

有一个技巧是动态开点：

考虑到线段树上每次区间操作最多找到 $log_n$ 个区间，当操作个数相对较少（ $10^5$ 左右）的时候，显然不是线段树上的每个节点都会被访问到的。

所以可以先不记录这些节点的编号，当我们访问到一个没有访问过的节点时，为这个节点赋予一个新的编号。

具体一点，对于点 $x$ ， $ch[x][2]$ 数组代表这个节点的左右两个儿子，当我们需要访问某个儿子时，若这个儿子为空（即为0），则将它的编号设置为一个没有出现过的编号。

这样的话空间复杂度就是 $O(nlog_m)$ 的了，其中 $n$ 为操作次数， $m$ 为序列长度。

代码如下：

void update(int &x,int l,int r,int val)
{
    if(!x)x=++tot;
    if(l>=L&&r<=R)
    {
        v[x]=max(v[x],val);
        return ;
    }
    int mid=(l+r)>>1;
    if(L<=mid)
    update(ch[x][0],l,mid,val);
    if(R>mid)
    update(ch[x][1],mid+1,r,val);
}

BZOJ 4636 蒟蒻的数列

线段树不止可以用于维护一个序列上的问题，它能做的事情真的是非常的多...下面说几个线段树相关的奇技淫巧♂

例 $5$

题意：给一个 $n$ 个点的无向图，但是边很多，以如下形式给出：

$(a,b)$ , $(c,d)$ 表示，对于任意两个点 $x,y$ ，如果 $a \leq x \leq b$ , $c \leq y \leq d$ ，那么在 $x,y$ 之间建造一条边，边权为 $1$
最后查询单源最短路。
这样的操作有 $m$ 次。
$n,m \leq 5 \times 10^5$

这个图真的很大，暴力建出来跑最短路死定了，时空双爆炸。
考虑利用线段树优化建图：

由于 $n$ 很大，直接建图一定无法接受... 但是我们发现数据给出的很有规律，都是一个区间向一个区间连边，所以可以让我们想到线段树。
具体是怎么优化建图的呢？我们建 $2$ 棵线段树，记为树 $A，B$ （接下连边均为单向边）
将树 $A$ 中的点连向父亲节点树 $B$ 中的点连向儿子节点树 $A,B$ 对应的叶子节点相连，这些边权均为 $0$ 。
此时从~~（心中的）~~ $B$ 树的任意一个节点都能以 $0$ 的距离到达该节点对应区间在 A 树上的节点

（对于给出的加边操作由于其为无向边，在进行下操作后进行一次反操作。）

对于每一个操作开一个新点从 $A$ 树的对应节点连向 $B$ 树的对应节点权值为 $\frac {1}{2}$ 这样做后，可以抽象 $A$ 树的每个叶子节点为原图中的点了
为什么可以呢，我们这样考虑：
首先在不开新点时 $A$ 树叶子节点是两两不可达的加入了新点后 $A$ 树叶子节点如果想抵达另一个叶子节点必须要经过如下流程： $A$ 树 -新点- $B$ 树- $A$ 树
那么这样的一条路径就和原图中的一条边一一对应了， $A$ 树中两叶子节点联通当且仅当它们在原图中可以互相抵达。然后就结束了，bfs 求最短路即可。

篇幅所限就这些内容了，线段树是所以基础数据结构中可变性最大的，也是最有趣的~
一些其他习题如下：

BZOJ 1636/1699 Balanced Lineup 排队
BZOJ 5039 [Jsoi2014] 序列维护
BZOJ 2770 YY 的 Treap
BZOJ 4631 踩气球
BZOJ 3939 [Usaco2015 Feb]Cow Hopscotch
BZOJ 3038 上帝造题的七分钟 2
BZOJ 2752 [HAOI2012] 高速公路 (road)

基本按照难度顺序给出。

主席树

终于到这里啦...

考古时间：
为什么主席树叫主席树呢？一定不是因为 OIER 们普遍崇拜江泽民主席...
hqdefault.jpg-19kB
事实上，主席树又名可持久化线段树，函数式线段树等奇怪的东西，被称呼为主席树主要是因为在国内，fotile 主席首先发明了这个数据结构。
为什么 fotile 被称作主席呢？因为他的真实姓名缩写是 HJT... ~~可惜不是 JZM~~

主席树超休闲的~

采用一个更形象具体的名字来称呼它：可持久化线段树。

什么叫可持久化呢？通俗的说，就是当我们每次对序列进行一次操作的时候，都修改了目前线段树的信息，我们记这个被修改后的的线段树为一个新的“版本”，在接下来的操作中，需要在线的对第 $i$ 个版本的线段树进行信息询问或修改成一个新的版本。

朴素的考虑怎么实现这个，我们直接大力存下每个版本的所有信息就行了...？
显然时空双爆炸。

哪里出现了问题呢？我们发现对线段树的一次操作只会修改 $log_n$ 个节点的信息，即根到某叶子节点的一条链。当区间操作的时候也是同理的。
所以实质上两个相邻版本的线段树的信息绝大部分都是一样的，为什么要都存下来呢？只要存下有哪些信息发生的变化即可，其他信息保持不变。
对于不变的某个子树，可以直接将父节点的儿子信息设为上一个版本的对应节点，这样就可以 $O(1)$ 的复制信息了。

代码写起来也超休闲的~

void update(int &x,int y,int l,int r,int pos)
{
    x=++tot;
    ch[x][0]=ch[y][0],ch[x][1]=ch[y][1],sum[x]=sum[y]+1;
    if(l==r)return ;
    int mid=(l+r)>>1;
    if(pos<=mid) update(ch[x][0],ch[y][0],l,mid,pos);
    else update(ch[x][1],ch[y][1],mid+1,r,pos);
}

这段代码实现了单点加和创建新版本的操作，实际实现中记录每个版本的根节点的标号就可以快速遍历这个版本了。

主席树使得我们可以记录“版本”信息，这有什么用呢？

用一个经典问题来辅助理解：

二维数点问题

初始给定平面上的 $n$ 个点，每次查询一个矩形内有多少个点。
$n \leq 5 \times 10^5 ， 1 \leq x_i,y_i \leq n$
强制在线。

我们考虑这个问题的一维情况：即给一个序列，问区间内有多少个点。

无语.jpg-4kB

修改操作都没有，普及选手都会做，维护前缀和即可。
如果想的话，可以线段树维护区间和。

啊！我会二维数点了！维护二维前缀和就好了！
无语.jpg-4kB
时空都是 $O(n^2)$ 的，所以从线段树的角度入手。

发现这样一个事实，我们可以简单的用线段树维护一行的信息，进一步，如果直接继承上一行的信息，我们可以简单的维护从第一行到目前行的前缀信息，每次加入在当前行的点即可。
如果查询矩形的底边均为 $y=1$ ，那么这个问题可以被轻易解决，然而不是。
可以很快想到用差分思想做这个事情，即将一个不贴底的矩形拆成两个贴底的矩形。
这样的话如果我们可以实时的保留第 $i$ 行和以前各行的线段树，问题就被简单解决了...！
主席树就可以做到这一点。

namespace seg
{
    int ch[N*40][2],sum[N*40],tot;
    void update(int &x,int y,int l,int r,int pos)
    {
        x=++tot;
        ch[x][0]=ch[y][0],ch[x][1]=ch[y][1],sum[x]=sum[y]+1;
        if(l==r)return ;
        int mid=(l+r)>>1;
        if(pos<=mid) update(ch[x][0],ch[y][0],l,mid,pos);
        else update(ch[x][1],ch[y][1],mid+1,r,pos);
    }
    int ask(int x,int l,int r,int L,int R)
    {
        if(l>=L&&r<=R)return sum[x];
        int mid=(l+r)>>1,ret=0;
        if(L<=mid) ret+=ask(ch[x][0],l,mid,L,R);
        if(R>mid)  ret+=ask(ch[x][1],mid+1,r,L,R);
        return ret;
    }
}

int now=1;
for(int i=1;i<=n;i++)
{
    root[i]=root[i-1];
    while(now<=cnt&&b[now].y==i)
    seg::update(root[i],root[i],1,n,b[now].x),now++;
}//每次加入当前行的点

点有权也可以一样的解决掉。
实质上是优化掉了树套树中的一层树。

时空复杂度均为 $O(nlog_n)$

下面考虑一些经典的问题：

例 $1$

题意： $n$ 个数， $m$ 次询问，对于每次询问，输出区间 $[l,r]$ 中第 $k$ 小的数是什么...
要求在线

无语.jpg-4kB

非常经典的问题，在线询问区间第 $k$ 小。
考虑对应权值维护一棵线段树，如果目前的集合里存在 $k$ 个权值为 $i$ 的点，则这棵线段树代表区间 $[i,i]$ 的叶子的区间和信息为 $k$ 。
这样的话，如果我们查询目前整个集合的第 $k$ 小，直接从根节点开始贪心的遍历即可。
具体方式是如果左子树内有超过 $k$ 个数，则答案一定在左子树内，否则向右子树遍历并带上目前左子树的贡献。
这样的话，如果所有询问的区间左端点均为 $1$ 就可以依次将目前的数加进线段树，并且处理以目前点为右端点的所有查询，可以做了。
这样就和刚刚的问题很像了，差分这个问题，用主席树维护历史版本的集合即可。

POJ 2104 K-th Number

例 $2$

题意： $n$ 个数， $m$ 次询问，对于每次询问，输出区间 $[l,r]$ 内是否存在严格众数，若存在，输出是什么
要求在线
$n,m \leq 5\times 10^5$

其中，严格众数定义为在区间内出现次数超过一半。

无语.jpg-4kB

和刚刚的问题很像，一样用主席树维护前缀版本的序列，在查询时，我们考虑左右儿子的元素个数。由于严格众数只可能在一边出现，所以直接判断一下然后找过去即可，若找不到，返回 $0$

BZOJ 3524 [Poi2014]Couriers

例 $3$

题意：询问树上路径第 k 小。
要求在线
$n,m \leq 5\times 10^5$

无语.jpg-4kB

把每一个点到根的路径建主席树，这样查询一个路径 $u-v$ 即相当于查询版本 $u+v-lca(u,v)-fa[lca(u,v)]$

然后就是经典问题了。

BZOJ 2588 Spoj 10628. Count on a tree

例 $4$

题意：n 个集合 m 个操作

操作：

$1$ $a$ $b$ 合并 $a$ , $b$ 所在集合
$2$ $k$ 回到第 $k$ 次操作之后的状态 (查询算作操作)
$3$ $a$ $b$ 询问 $a$ , $b$ 是否属于同一集合，是则输出 $1$ ，否则输出 $0$

实际上就是实现一个可持久化并查集。
$n,m \leq 5\times 10^5$

无语.jpg-4kB

通过主席树可以实现 可持久化数组 ，并查集其实就是记录了一个 $fa$ 数组... 那么可持久化 $fa$ 一下就是可持久化并查集了...

具体可以看代码...

BZOJ [3673/3674] [可持久化并查集 by zky]/[可持久化并查集加强版]

例 $5$

题意：
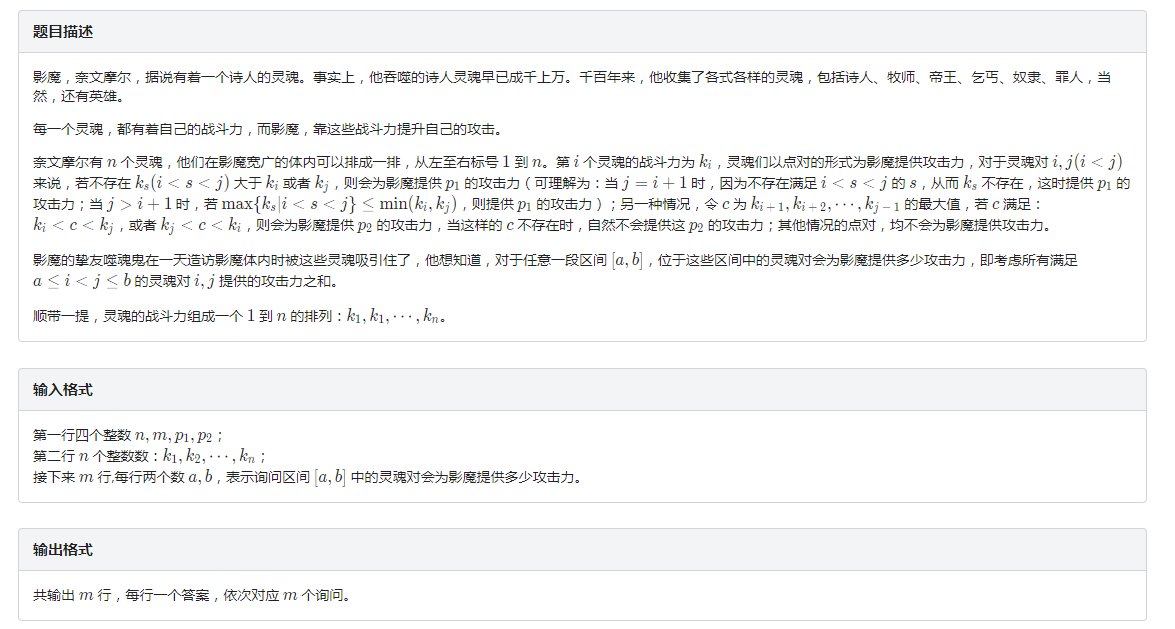
ym.png-91.5kB
YMM.png-4.6kB

无语.jpg-4kB

记 $pre_i$ 和 $nxt_i$ 分别表示 $i$ 前后第一个比它大的数的位置。
首先考虑第一种贡献，发现符合条件的点对只有 $O(n)$ 个，即对于数 $i$ , $(pre_i,nxt_i)$ 组成了它。
这个可以用简单的二维数点去维护。
那么考虑第二种贡献，显然为了满足单调性，区间端点一定包含 $pre_i$ 和 $nxt_i$ 的其中一个。
然后考虑确定了 $i$ 和一个端点，另一个端点最远可以延伸到哪里，这个其实就是另一个端点 $+1$ 或者 $-1$ 。
也就是说，第二种贡献的可行点对是一个固定一个端点的连续区间，体现在平面上就是一条与坐标轴平行的线段。
这个怎么维护呢？
考虑如果只有横向的线段，正常维护主席树，每次遇到线段区间加即可。
有纵向的？再开一棵主席树，分别维护行列就行了。
主席树的区间修改也需要动态开点，或者干脆标记永久化。

BZOJ 4826 [Hnoi2017] 影魔

另外的一些习题：
BZOJ 3123 [Sdoi2013] 森林
BZOJ 4771 七彩树

真的超休闲的。

树套树

课件

K-Dtree

这个数据结构讲课内容里没有，但是我很喜欢，所以加进来了。

课件

写在后面的话

数据结构的世界多彩缤纷，我只向大家揭露了她的冰山一角。
希望能够引起大家的兴趣，使得大家喜欢上美妙的数据结构，为数据结构大厦的建成添砖加瓦。
在OI的道路上越走越远，目标是成为数据结构大师！

最后祝大家在接下来一周的中学习顺利，考试全AK~

顺便再宣一下个人博客，这里面可以找到上文提到的所有例题的题解和代码。

基础数据结构杂谈

写在前面的话

Q&A

数据结构

单调栈

栈

单调栈

例 1

树状数组

一个比较常见的小技巧：树状数组维护区间加和区间求和。

例 1

例 2

线段树

普通线段树：

文艺线段树：

例 1

例 2

例 3

例 4

例 5

主席树

二维数点问题

例 1

例 2

例 3

例 4

例 5

树套树

K-Dtree

写在后面的话

内容目录

例 $1$

例 $1$

例 $2$

例 $1$

例 $2$

例 $3$

例 $4$

例 $5$

例 $1$

例 $2$

例 $3$

例 $4$

例 $5$