《算法与数据结构》学习笔记：树状数组

树状数组 前缀和

---

一、树状数组能解决的问题

树状数组，也称作“二叉索引树”（Binary Indexed Tree）或 Fenwick 树。 它可以高效地实现如下两个操作：

1、数组前缀和的查询；

2、单点更新。

下面具体解释这两个操作。

1、 数组前缀和的查询

首先看下面这个例子，了解什么是数组的前缀和查询。

例1：已知数组 $[10, 15, 17, 19, 20, 14, 12]$。

1、求索引 $0$ 至索引 $4$ 的所有元素的和；
2、求索引 $0$ 至索引 $5$ 的所有元素的和；
3、求索引 $0$ 至索引 $7$ 的所有元素的和。

“前缀和”定义了一个数组从“头”开始的区间，计算的是这个从索引位置是 $0$ 开始的区间中的所有元素的“和”。

注意：我们的基本问题是解决从索引位置是 $0$ 开始的所有元素的和，而其它不是从 $0$ 开始的数组的区间和可以转化成前面的这个问题。这一点可以看后面的例 4 。

2、单点更新

例 2：已知数组 $[10, 15, 17, 19, 20, 14, 12]$ 。

1、将索引为 $4$ 的元素增加 $2$；
2、将索引为 $6$ 的元素减少 $3$。

“单点更新”定义了将数组指定索引的元素值变更为另一个值，给出的参数是一个改变的数值，即“更新以后的值-原来的值”。注意，单点更新的操作，我们描述的是“相对于之前的值发生的变化”，而不是“变成了什么”。

如果我们不使用任何数据结构，仅依靠定义，“数组前缀和的查询 ” 的时间复杂度是 $O(n)$，“单点更新” 的时间复杂度是 $O(1)$。
我们觉得“数组前缀和的查询 ” 的时间复杂度较大，要扫描这个区间的一大部分元素，才能得到这个区间的和。于是一个常见的做法是，我们可以首先计算出一个“前缀和数组”，这个数组的每个元素的值对应的正是原来数组的前缀和。

例3：已知数组 nums = [1, 2, 3, 4, 5, 6, 7]，求前缀和数组 cumsum。

分析：根据前缀和的定义，容易计算前缀和数组是 cumsum = [1, 3, 6, 10, 15, 21, 28]。

有了前缀和数组每次查询前缀和时间复杂度就变成了 $O(1)$。前缀和数组得到以后，就可以以 $O(1)$ 的时间复杂度解决“区间和”问题。

例4：已知数组 nums = [1, 2, 3, 4, 5, 6, 7] ，求区间 [3, 7] 的和，特别说明：该例中数组的索引从 $1$ 开始计算。

说明：注意到这个例子有一个特别说明“该例中数组的索引从 $1$ 开始计算”，大家先不要纠结为什么。因为后续我们对树状数组的定义都选择从索引 $1$ 开始，这和堆的一般实现思想类似，索引 $0$ 我们不放元素。这个例子只是为了说明“已知前缀和可以用 $O(1)$ 的时间复杂度得到区间和”。

分析：由于“前缀和(7)” = nums[1] + nums[2] + nums[3] + nums[4] + nums[5] + nums[6] + nums[7] ；
“前缀和(2)” = nums[1] + nums[2]；
而“区间 [3, 7] 的和”= nums[3] + nums[4] + nums[5] + nums[6] + nums[7]；
所以，“区间 [3, 7] 的和” = “前缀和(7)” - “前缀和(2)” 。

从这个例子中，我们可以看出：前缀和数组知道了，区间和也可以很快地求出来。

那如果我要执行“单点更新”，就得更新这个前缀和数组，又得计算一次前缀和，时间复杂度为 $O(n)$。
那如果我在一次业务场景中“前缀和”和“单点更新”的次数都很多，前缀和数组就不高效了。而 Fenwick 树就是“高效的”实现“前缀和”和“单点更新”这两个操作的数据结构。

二、树状数组长什么样子

我们首先先看看树状数组长什么样，有一个直观的认识。

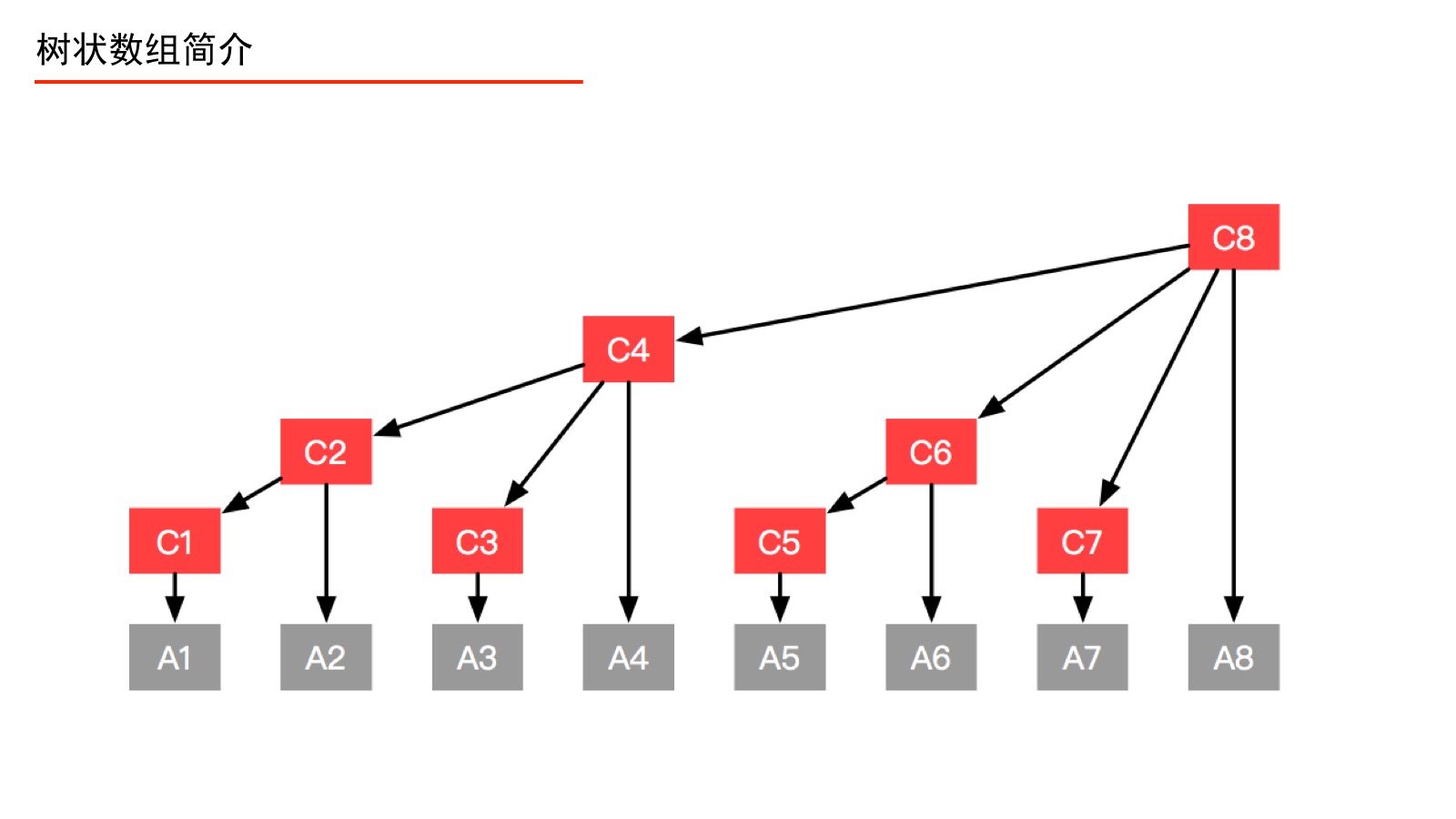
例5：我们以一个有 $8$ 个元素的数组 A 为例（如上图），在数组 A 之上建立一个数组 C，使得数组 C 的形成如上的一个多叉树形状，数组 C 就是一个树状数组。此时我们有以下疑问：

• 1、树状数组要建成动态的树形结构吗？

  分析：不。学习过堆、线段树的朋友一定知道，使用数组就能方便地索引左右孩子结点、双亲结点（因为规律特别容易找到），这样的树就不必创建成结点、指针那样的动态树形结构。

• 2、如何解释“前缀和查询”、“单点更新”？
  分析：例如我们要查询“前缀和(4)”，本来应该问 A1、A2、A3、A4，有了数组 C 之后，我们只要问 C4 即可。再如，我们要更新结点 A1 的值，只要自底向上更新 C1、C2、C4、C8 的值即可。

补充说明：这一段看不明白没有关系，耐着性子往后看。我们构件好 数组 C 以后，就完全可以抛弃数组 A 了。

在这个小数组中，可能我们无法体会到 Fenwick 树的威力，请大家稍安勿躁，学习到后面，你就知道为什么 Fenwick 树对于“前缀和查询”和“单点更新”都非常频繁的业务来说是高效的。

三、理解数组 C 的定义

首先我们强调一下，树状数组的下标从 $1$ 开始计数，这一点我们看到后面就会很清晰了。我们先了解如下的定义，请大家一定先记住这些记号所代表的含义：

1、数组 C 是一个对原始数组 A 的预处理数组。

2、我们还要熟悉几个记号。为了方便说明，避免后面行文啰嗦，我们将固定使用记号 $i$ 、$j$ 、 $k$，它们的定义如下：
记号 $i$ ：表示预处理数组 $C$ 的索引（十进制表示）。
记号 $j$ ：表示原始数组 $A$ 的索引（十进制表示）。
我们通过以下的图，来看看 C1、C2、C3、C4、C5、C6、C7、C8 分别是如何定义的。

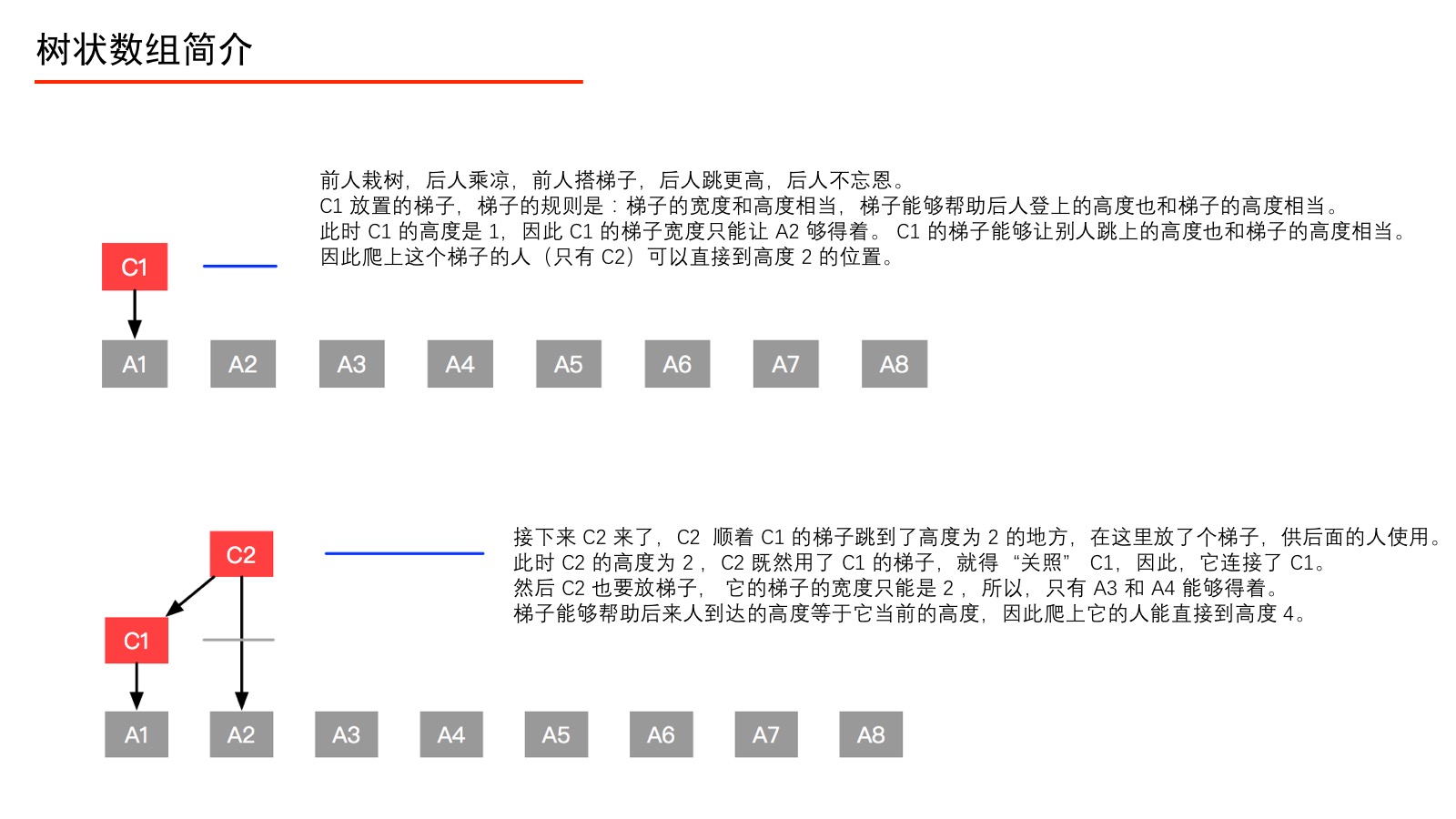
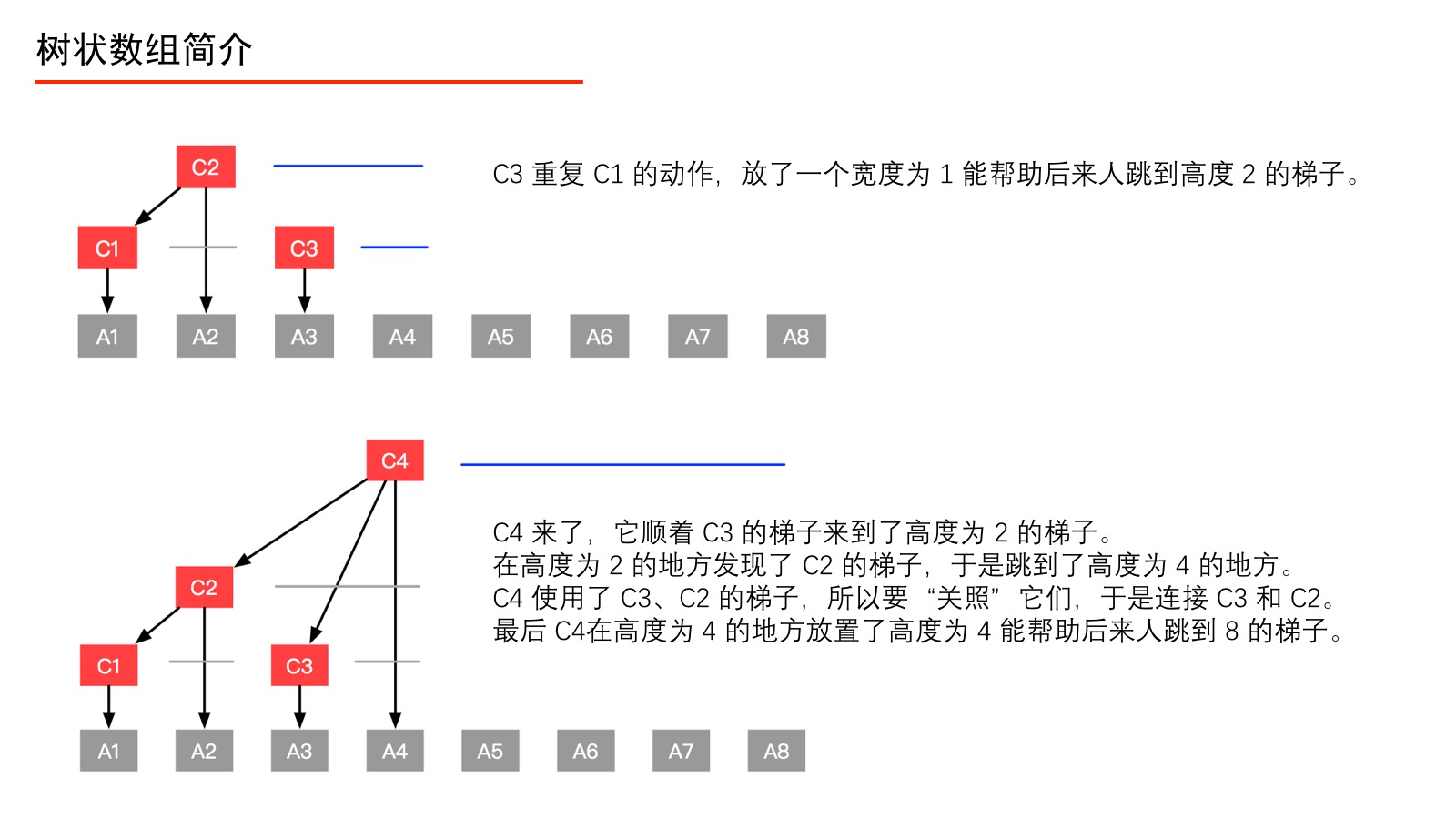
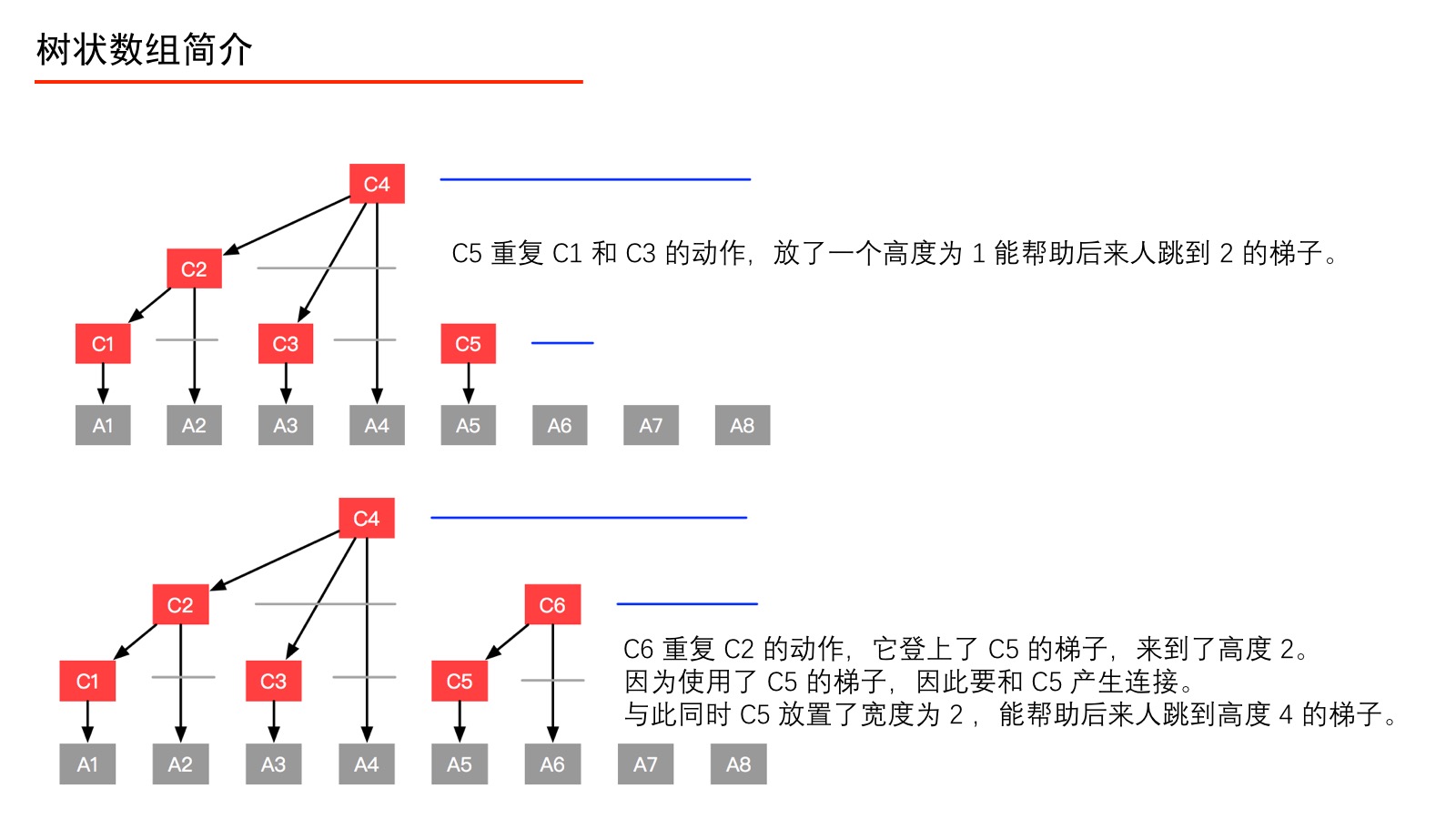
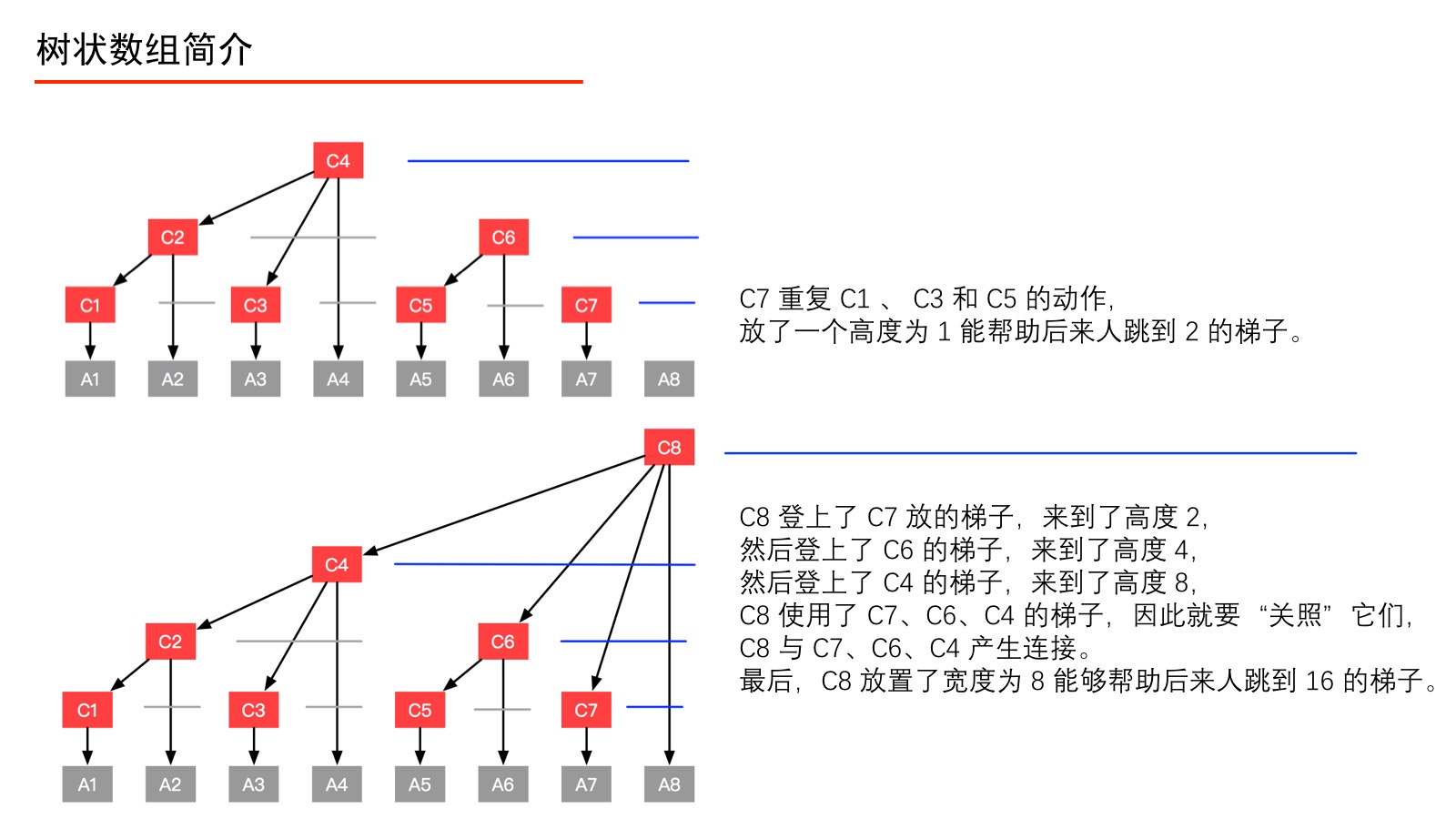
上面的过程我们用如下的表来表示。

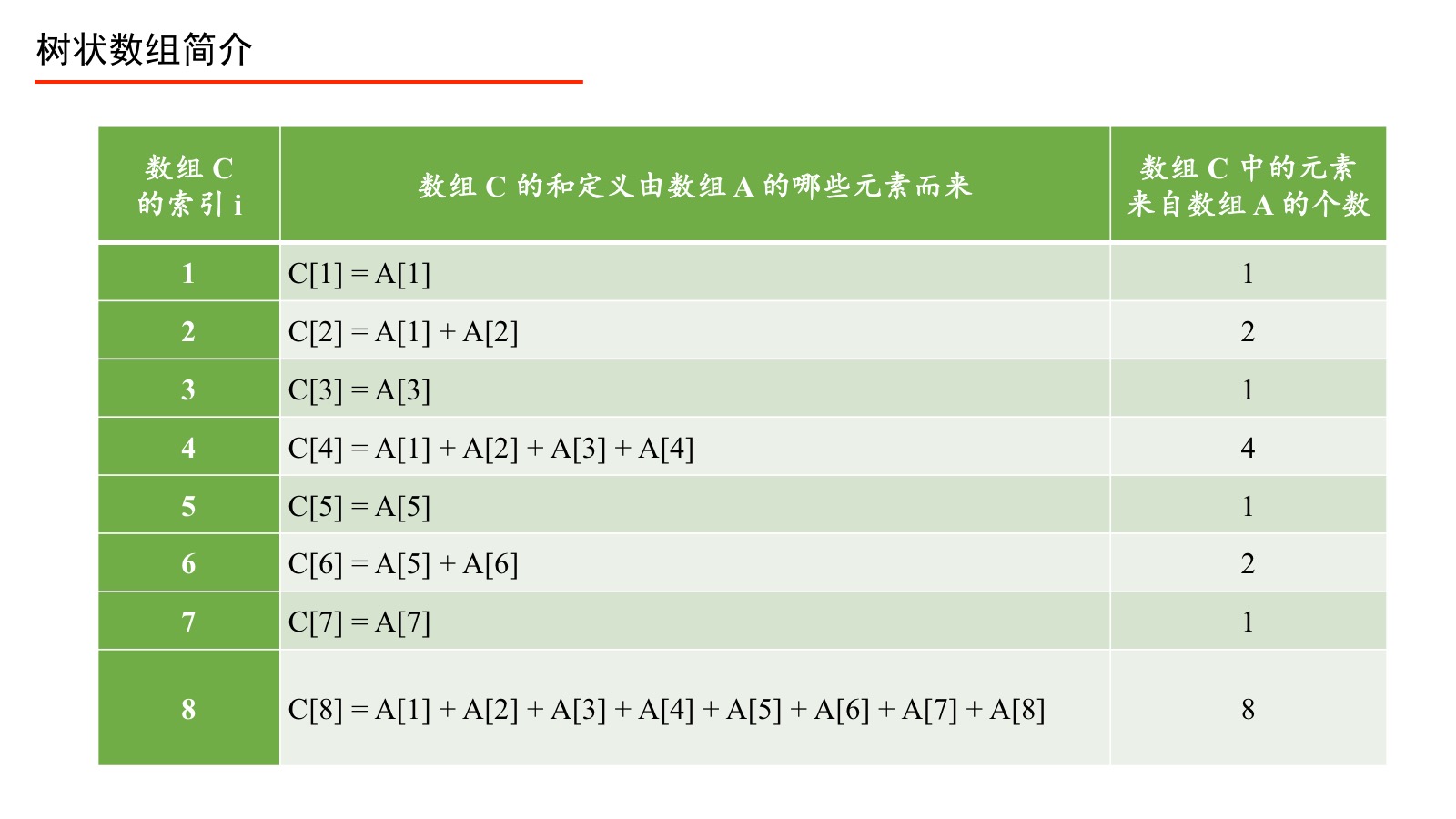
四、数组 $C$ 的索引与数组 $A$ 的索引的关系

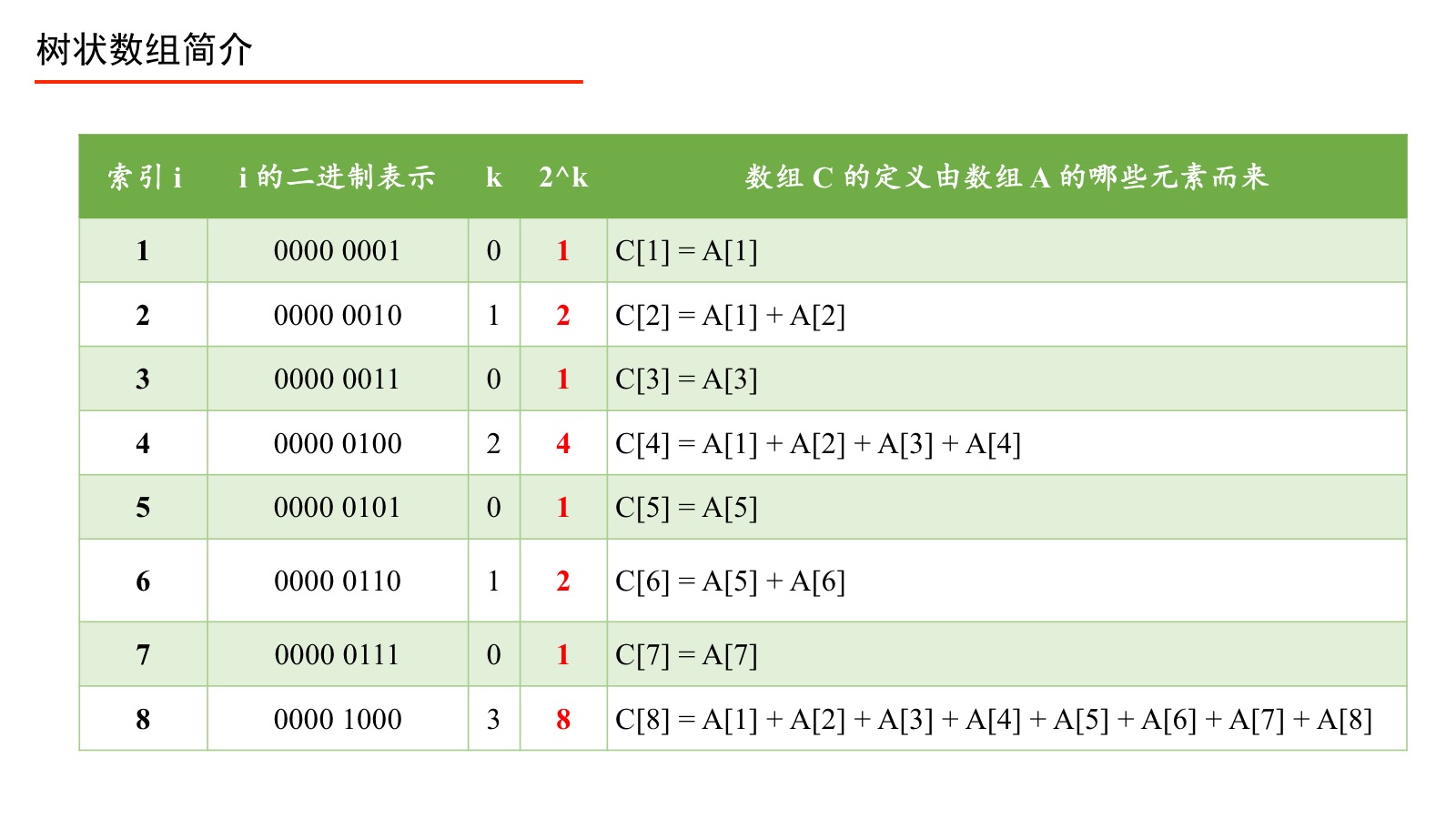
伟大的计算机科学家注意到上表中标注了“数组 $C$ 中的元素来自数组 $A$ 的元素个数”，它们的规律如下：将数组 $C$ 的索引 $i$ 表示成二进制，从右向左数，遇到 $1$ 则停止，数出 $0$ 的个数记为 $k$，则计算 $2^k$ 就是“数组 $C$ 中的元素来自数组 $A$ 的个数”，并且可以具体得到来自数组 $A$ 的表示，即从当前索引 $i$ 开始，从右向前数出 $2^k$ 个数组 $A$ 中的元素的和，即组成了 $C[i]$。下面具体说明。

记号 $k$ ：将 $i$ 的二进制表示从右向左数出的 $0$ 的个数，遇到 $1$ 则停止，记为 $k$。 我们只对数组 $C$ 的索引 $i$ 进行这个计算，数组 $A$ 的索引 $j$ 不进行相应的计算。理解 $k$ 是如何得到的是关键，请务必重视。下面我们通过两个例子进行说明。

例5：当 $i = 5$ 时，计算 $k$。

分析：因为 $5$ 的二进制表示是 $0000\;0101$，从右边向左边数，第 $1$ 个是 $1$ ，因此 $0$ 的个数是 $0$，此时 $k=0$ 。

例6：当 $i = 8$ 时，计算 $k$。

分析：因为 $8$ 的二进制表示是 $0000\;1000$，从右边向左边数遇到 $1$ 之前，遇到了 $3$ 个 $0$，此时 $k$ = 3。

计算出 $k$ 以后，$2^k​$ 立马得到，为此我们可以画出如下表格：

我们看到 $2^k$ 是我们最终想要的。下面我们介绍一种很酷的操作，叫做 lowbit ，它可以高效地计算 $2^k$，即我们要证明：

$${\rm lowbit}(i) = 2^k$$

其中 $k$ 是将 $i$ 表示成二进制以后，从右向左数，遇到 $1$ 则停止时，数出的 $0$ 的个数。

五、通过 lowbit 操作高效计算 $2^k$

lowbit(i) = i & (-i)

对，就是这么简单。理解这行伪代码需要一些二进制和位运算的知识作为铺垫。

首先，我们知道负数的二进制表示为：相应正数的二进制表示的反码 + 1。

例7：计算 $-6$ 的二进制表示。

分析：$6$ 的二进制表示为 $0000\;0110$，先表示成反码，即“ $0$ 变 $1$，$1$ 变 $0$”，得 $1111\;1001$，再加 $1$，得 $1111\;1010$。

例8：当 i = 6 时，计算 ${\rm lowbit}(i)​$ 。

分析：由例 7 及“与”运算的定义，把它们按照数位对齐上下写好：

0000 0110
1111 1010
0000 0010

说明：上下同时为 $1​$ 才写 $1​$，否则写 $0​$，最后得到 0000 0010，这个二进制数表示成十进制数就是 $2​$。建议大家多在稿纸上写几个具体的例子来计算 ${\rm lowbit}​$，进而理解为什么 ${\rm lowbit}(i)=2^k​$。

下面我给出一个我的直观解释：如果我们直接将一个整数“按位取反”，再与原来的数做“与”运算，一定得到 $0$。巧就巧在，负数的二进制表示上，除了要求对“按位取反”以外，还要“加” $1$，在“加 ” $1$ 的过程中产生的进位数即是“将 $i$ 表示成二进制以后，从右向左数，遇到 $1$ 停止时数出 $0$ 的个数”。

那么我们知道了 ${\rm lowbit}$ 以后，又有什么用呢？由于位运算是十分高效的，它能帮助我们在树状数组中高效计算“从子结点索引到双亲节点”（即对应“单点更新”操作），高效计算“前缀和由预处理数组的那些元素表示”（即对应“前缀和查询操作”）。

六、体会 lowbit 的魅力所在

1、 “单点更新”操作：“从子结点到父节点”

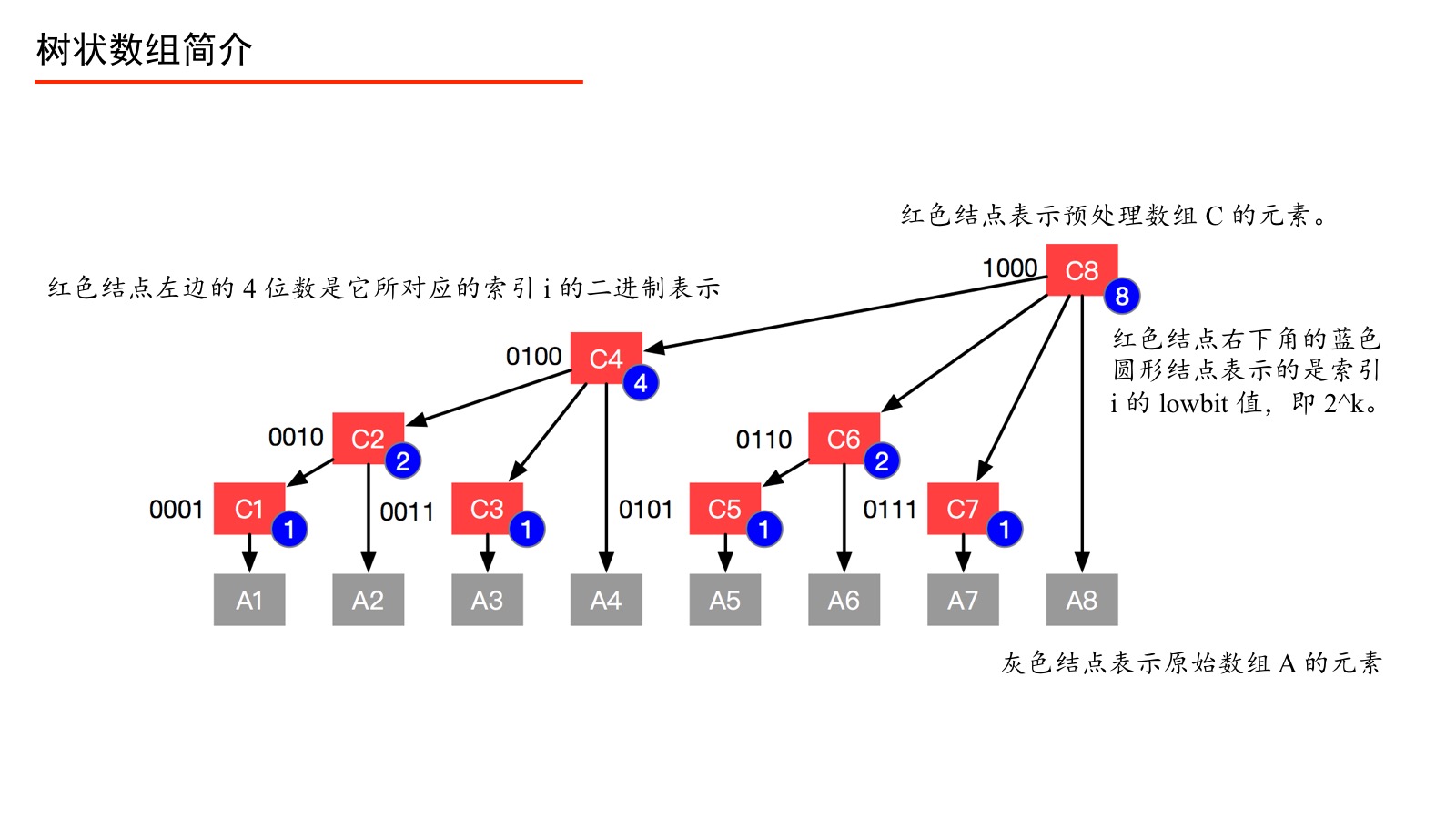
例9：修改 $A[3]​$， 分析对数组 $C​$ 产生的变化。

从图中我们可以看出 $A[3]$ 的父结点以及祖先结点依次是 $C[3]$、$C[4]$、$C[8]$ ，所以修改了 $A[3]$ 以后 $C[3]$、$C[4]$、$C[8]$ 的值也要修改。

先看 $C[3]​$ ，${\rm lowbit}(3) = 1​$， $3 + {\rm lowbit}(3) = 4​$ 就是 $C[3]​$ 的父亲结点 $C[4]​$ 的索引值。
再看 $C[4]​$ ，${\rm lowbit}(4) = 4​$， $4 + {\rm lowbit}(4) = 8​$ 就是 $C[4]​$ 的父亲结点 $C[8]​$ 的索引值。
从图中，也可以验证：“红色结点的索引值 + 右下角蓝色圆形结点的值 = 红色结点的双亲结点的索引值”。

下面我试图解释这个现象：$3$ 即 $0011$，从右向左，遇到 $0$ 放过，遇到 $1$ 为止，给这个数位加 $1$，这个操作就相当于加上了一个 $2^k$ 的二进制数，即一个 ${\rm lowbit}$ 值，有意思的事情就发生在此时，马上就发发生了进位，得到 $0100$，即 $4$ 的二进制表示。
接下来处理 $0100$，从右向左，从右向左，遇到 $0$ 放过，遇到 $1$ 为止，给这个数位加 $1$，同样地，这个操作就相当于加上了一个 $2^k$ 的二进制数，即一个 ${\rm lowbit}$ 值，可以看到，马上就发发生了进位，得到 $1000$，即 $8$ 的二进制表示。

从我上面的描述中，你可以发现，我们又在做“从右边到左边数，遇到 $1$ 之前数出 $0$ 的个数”这件事情了，
由此我们可以总结出规律：从已知子结点的索引 $i$ ，则结点 $i$ 的父结点的索引 ${\rm parent}$ 的计算公式为：

$${\rm parent}(i) = i + {\rm lowbit}(i)$$

可不过我还想说明的是，这不是巧合和循环论证，这正是因为对 “从右边到左边数出 $0$ 的个数，遇到 $1$ 停止这件事情”的定义，使用 ${\rm lowbit}$ 可以快速计算这件事成立，才会有的。

分析到这里“单点更新”的代码就可以马上写出来了。

/**
 * 单点更新
 *
 * @param i     原始数组索引 i
 * @param delta 变化值 = 更新以后的值 - 原始值
 */
public void update(int i, int delta) {
    // 从下到上更新，注意，预处理数组，比原始数组的 len 大 1，故 预处理索引的最大值为 len
    while (i <= len) {
        tree[i] += delta;
        i += lowbit(i);
    }
}
public static int lowbit(int x) {
    return x & (-x);
}

2、 “前缀和查询操作”：计算前缀和由预处理数组的那些元素表示”

还是上面那张图。

例 10 ：求出“前缀和(6)”。

由图可以看出“前缀和(6) ” = $C[6]$ + $C[4]$。

先看 $C[6]$ ，${\rm lowbit}(6) = 2$， $6 - {\rm lowbit}(6) = 4$ 正好是 $C[6]$ 的上一个非叶子结点 $C[4]$ 的索引值。这里给出我的一个直观解释，如果下标表示高度，那么上一个非叶子节点，其实就是从右边向左边画一条水平线，遇到的墙的索引。只要这个值大于 $0​$，都能正确求出来。

例11：求出“前缀和(5)”。

再看 $C[5]$ ，${\rm lowbit}(5) = 1$， $5 - {\rm lowbit}(6) = 4$ 正好是 $C[5]$ 的上一个非叶子结点 $C[4]$ 的索引值，故“前缀和(5)” = $C[5]$ + $C[4]$。

例12：求出“前缀和(7)”。

再看 $C[7]$ ，${\rm lowbit}(7) = 1$， $7 -{\rm lowbit}(7) = 6$ 正好是 $C[7]$ 的上一个非叶子结点 $C[6]$ 的索引值，再由例9 的分析，“前缀和(7)” =$C[7]$ + $C[6]$ + $C[4]​$。

例13：求出“前缀和(8)”。

再看 $C[8]$ ，${\rm lowbit}(8) = 8$， $8 - {\rm lowbit}(8) = 0$ ， $0$ 表示没有，从图上也可以看出从右边向左边画一条水平线，不会遇到的墙，故“前缀和(8)” = $C[8]​$ 。

经过以上的分析，求前缀和的代码也可以写出来了。

/**
 * 查询前缀和
 *
 * @param i 前缀的最大索引，即查询区间 [0, i] 的所有元素之和
 */
public int query(int i) {
    // 从右到左查询
    int sum = 0;
    while (i > 0) {
        sum += tree[i];
        i -= lowbit(i);
    }
    return sum;
}

可以看出“单点更新”和“前缀和查询操作”的代码量其实是很少的。

三、树状数组的初始化

这里要说明的是，初始化前缀和数组应该交给调用者来决定。下面是一种初始化的方式。树状数组的初始化可以通过“单点更新”来实现，因为“最最开始”的时候，数组的每个元素的值都为 $0$，每个都对应地加上原始数组的值，就完成了预处理数组 $C$ 的创建。
这里要特别注意，update 操作的第 $2$ 个索引值是一个变化值，而不是变化以后的值。因为我们的操作是逐层上报，汇报变更值会让我们的操作更加简单，这一点请大家反复体会。

public FenwickTree(int[] nums) {
    this.len = nums.length + 1;
    tree = new int[this.len + 1];
    for (int i = 1; i <= len; i++) {
        update(i, nums[i]);
    }
}

基于以上所述，树状数组的完整代码已经可以写出来了。

Java 代码：

public class FenwickTree {
    /**
     * 预处理数组
     */
    private int[] tree;
    private int len;
    public FenwickTree(int n) {
        this.len = n;
        tree = new int[n + 1];
    }
    /**
     * 单点更新
     *
     * @param i     原始数组索引 i
     * @param delta 变化值 = 更新以后的值 - 原始值
     */
    public void update(int i, int delta) {
        // 从下到上更新，注意，预处理数组，比原始数组的 len 大 1，故 预处理索引的最大值为 len
        while (i <= len) {
            tree[i] += delta;
            i += lowbit(i);
        }
    }
    /**
     * 查询前缀和
     *
     * @param i 前缀的最大索引，即查询区间 [0, i] 的所有元素之和
     */
    public int query(int i) {
        // 从右到左查询
        int sum = 0;
        while (i > 0) {
            sum += tree[i];
            i -= lowbit(i);
        }
        return sum;
    }
    public static int lowbit(int x) {
        return x & (-x);
    }
}

Python 代码：

class FenwickTree:
    def __init__(self, n):
        self.size = n
        self.tree = [0 for _ in range(n + 1)]
    def __lowbit(self, index):
        return index & (-index)
    # 单点更新：从下到上，最多到 size，可以取等
    def update(self, index, delta):
        while index <= self.size:
            self.tree[index] += delta
            index += self.__lowbit(index)
    # 区间查询：从上到下，最少到 1，可以取等
    def query(self, index):
        res = 0
        while index > 0:
            res += self.tree[index]
            index -= self.__lowbit(index)
        return res

四、树状数组的应用

例题1：《剑指 Offer 》第 51 题：逆序数的计算

传送门：数组中的逆序对。

要求：在数组中的两个数字如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。

输入一个数组，求出这个数组中的逆序对的总数。

样例

输入：[1,2,3,4,5,6,0]
输出：6

分析：这道题最经典的思路是使用分治法计算，不过使用树状数组语义更清晰一些。

class Solution(object):
    def inversePairs(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        class FenwickTree:
            def __init__(self, n):
                self.size = n
                self.tree = [0 for _ in range(n + 1)]
            def __lowbit(self, index):
                return index & (-index)
            # 单点更新：从下到上，最多到 size，可以取等
            def update(self, index, delta):
                while index <= self.size:
                    self.tree[index] += delta
                    index += self.__lowbit(index)
            # 区间查询：从上到下，最少到 1，可以取等
            def query(self, index):
                res = 0
                while index > 0:
                    res += self.tree[index]
                    index -= self.__lowbit(index)
                return res
        # 特判
        l = len(nums)
        if l < 2:
            return 0
        # 原始数组去除重复以后从小到大排序
        s = list(set(nums))
        # 构建最小堆，因为从小到大一个一个拿出来，用堆比较合适
        import heapq
        heapq.heapify(s)
        # 由数字查排名
        rank_map = dict()
        index = 1
        # 不重复数字的个数
        size = len(s)
        for _ in range(size):
            num = heapq.heappop(s)
            rank_map[num] = index
            index += 1
        res = 0
        # 树状数组只要不重复数字个数这么多空间就够了
        ft = FenwickTree(size)
        # 从后向前看，拿出一个数字来，就更新一下，然后向前查询比它小的个数
        for i in range(l - 1, -1, -1):
            rank = rank_map[nums[i]]
            ft.update(rank, 1)
            res += ft.query(rank - 1)
        return res

说明：中间将数字映射到排名是将原数组“离散化”，“离散化”的原因有 2 点：

1、树状数组我们看到，索引是从“$1$”开始的，我们不能保证我们的数组所有的元素都大于等于 $1$；

2、即使元素都大于等于“$1$”，为了节约树状数组的空间，我们将之“离散化”可以把原始的数都压缩到一个小区间。我说的有点不太清楚，这一点可以参考 树状数组 求逆序数 poj 2299。

例2：LeetCode 第 315 题：计算右侧小于当前元素的个数

要求：给定一个整数数组 nums，按要求返回一个新数组 counts。数组 counts 有该性质： counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。

示例:

输入: [5,2,6,1]
输出: [2,1,1,0]
解释:
5 的右侧有 2 个更小的元素 (2 和 1).
2 的右侧仅有 1 个更小的元素 (1).
6 的右侧有 1 个更小的元素 (1).
1 的右侧有 0 个更小的元素.

思路：“计算右侧小于当前元素的个数”我们可以“从后向前一个一个填”。因为涉及大小关系，所以要排个序，并且给出序号。这一步操作也叫“离散化”。具体方法是：先画出一个排名表，对于这个问题，排名表是：

数	排名
1	1
2	2
5	3
6	4

从后向前填：

1、遇到 1 ，1 的排名是 1 ，首先先在 1 那个位置更新 1，那么 1 之前肯定没有数了，所以就是 0；

2、遇到 6 ， 6 的排名是 4，首先先在 4 那个位置更新 1，那么 6 之前可以在树状树组里面查一下，是 1；

3、遇到 2 ， 2 的排名是 2，首先先在 2 那个位置更新 1，那么 2 之前可以在树状树组里面查一下，是 1；

4、遇到 5 ，5 的排名是 3，首先先在 3 那个位置更新 1，那么 3 之前可以在树状树组里面查一下，是 2；

反过来就是结果 [2,1,1,0]。

Python 代码：

class Solution:
    def countSmaller(self, nums):
        """
        :type nums: List[int]
        :rtype: List[int]
        """
        class FenwickTree:
            def __init__(self, n):
                self.size = n
                self.tree = [0 for _ in range(n + 1)]
            def __lowbit(self, index):
                return index & (-index)
            # 单点更新：从下到上，最多到 size，可以取等
            def update(self, index, delta):
                while index <= self.size:
                    self.tree[index] += delta
                    index += self.__lowbit(index)
            # 区间查询：从上到下，最少到 1，可以取等
            def query(self, index):
                res = 0
                while index > 0:
                    res += self.tree[index]
                    index -= self.__lowbit(index)
                return res
        l = len(nums)
        if l == 0:
            return []
        if l == 1:
            return [0]
        s = list(set(nums))
        import heapq
        heapq.heapify(s)
        index = 1
        size = len(s)
        rank_map = dict()
        ft = FenwickTree(size)
        for _ in range(size):
            num = heapq.heappop(s)
            rank_map[num] = index
            index += 1
        # 从后向前填表
        res = [None for _ in range(l)]
        for index in range(l - 1, -1, -1):
            rank = rank_map[nums[index]]
            ft.update(rank, 1)
            res[index] = ft.query(rank - 1)
        return res

五、扩展与参考资料

1、扩展

下面这个课件提到了树状数组深入的使用技巧和二维树状数组：

https://wenku.baidu.com/view/1bc0aa1852d380eb62946db0.html?from=search

我没有精力继续研究了，毕竟我不搞算法竞赛，有时间再看。

2、参考资料

编写本文参考了以下网络资源：

【算法】逆序对问题的四种解法（归并排序，BST，树状数组，线段树）及变形
https://blog.csdn.net/haolexiao/article/details/54989306

leetcode 315 Count of Smaller Numbers After Self 以及 BST总结。
https://segmentfault.com/a/1190000008233783

poj 2299 Ultra-QuickSort 求逆序数，树状数组解法，详细解析
https://blog.csdn.net/Lionel_D/article/details/43535741

白话数据结构
https://blog.csdn.net/column/details/acxxz.html

（完）