[关闭]
@onejune 2021-10-15T00:03:06.000000Z 字数 9136 阅读 2083

MindAlpha系列(7)-ctr&cvr联合预估之EESMM

MindAlpha FTRL ESMM cvr

0.目录

1.问题背景

样本选择偏差 Sample selection bias (SSB)

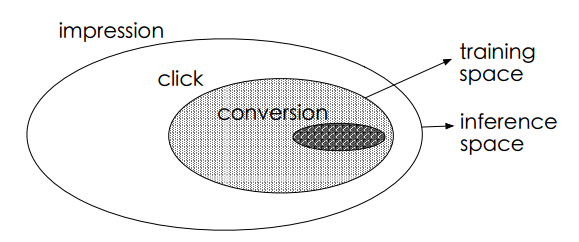
image_1dabfknfru8514df153t8ua1hd59.png-34.1kB
如图所示，最外面的大椭圆为整个样本空间S，其中有点击的事件（y=1）的样本组成的集合为,对应图中的阴影区域。传统的cvr模型是使用图中的阴影区域训练得到的，同时训练好的cvr模型又需要在整个样本空间做预估。

由于点击事件相对展现事件要少很多，因此只是样本空间S的一个很小的子集，从上提取的特征相对于从S中提取到哦特征而言是有偏的，甚至是很不相同。从而，按这种方法构建的训练样本集相当于是从一个与真实分布不一致的分布中采样得到的，这一定程度上违背了机器学习算法之所以有效的前提：训练样本与测试样本必须独立地采样自同一个分布，即独立同分布的假设。

训练样本从整体样本空间的一个较小子集中提取，而训练得到的模型却需要对整个样本空间中的样本做推断预测的现象称之为样本选择偏差。样本选择偏差会伤害学到的模型的泛化性能。

数据稀疏 Data sparsity (DS)

推荐系统展现给用户的广告数量要远远大于被用户点击的广告数量，同时有点击行为的用户也仅仅只占所有用户的一小部分，因此有点击行为的样本空间相对于整个样本空间来说是很小的，通常来讲，量级要少1~3个数量级。在淘宝公开的训练数据集上，只占整个样本空间的4%。而对Mobvista的normal广告来说，这个比例只有0.8%。这就是所谓的训练数据稀疏的问题，高度稀疏的训练数据使得模型的学习变得相当困难。

2.ESMM解决的问题

ESMM模型利用用户行为序列数据，在完整的样本数据空间同时学习点击率和转化率（post-view clickthrough&conversion rate，CTCVR），解决了传统CVR预估模型难以克服的样本选择偏差（sample selection bias）和训练数据过于稀疏（data sparsity ）的问题。

用户在观察到系统展现的推荐商品列表后，可能会点击自己感兴趣的商品，进而产生购买行为。换句话说，用户行为遵循一定的顺序决策模式：impression → click → conversion。 CVR模型旨在预估用户在观察到曝光商品进而点击到商品详情页之后购买此商品的概率，即pCVR = p(conversion|click,impression)。


ESMM的做法是：pCVR在先估计出pCTR和pCTCVR之后推导出来。相当于分别单独训练两个模型拟合出pCTR和pCTCVR，再通过pCTCVR除以pCTR 得到最终的拟合目标pCVR。pCTR和pCTCVR是ESMM模型需要估计的两个主要因子，而且是在整个样本空间上建模得到的，pCVR只是一个中间变量。由此可见，ESMM模型是在整个样本空间建模，而不像传统CVR预估模型那样只在点击样本空间建模。

3.损失函数及梯度推导

损失函数


其中，和分别是CTR网络和CVR网络的参数，是交叉熵损失函数。在CTR任务中，有点击行为的展现事件构成的样本标记为正样本，没有点击行为发生的展现事件标记为负样本；在CTCVR任务中，同时有点击和购买行为的展现事件标记为正样本，否则标记为负样本。

梯度推导

将(1)分成两部分：


已知:
令，则即：

针对单条训练样本进行梯度推导：将(2)代入(1)得到：
for ctr:
损失函数展开：

然后对θ求导：

for ctcvr:
损失函数展开：
我们令

则有：

于是：

综上可得：


对的梯度：

对的梯度：

4.直观理解

对于(23)和(25)式：
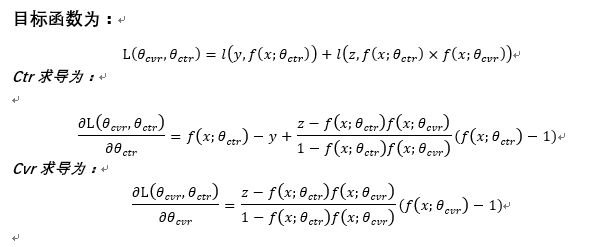
微信图片_20181110222720.png-13.2kB

下面对y和z的取值分情况讨论：
(1) 当z=1时，必有y=1(有转化必定有点击)：


此时ctr的梯度会变为原始的2倍，相当于有转化的点击加大样本的权重；cvr与原始更新一致。

(2)当z=0时:

cvr的梯度公式为：


其中
与原始梯度比较：

ctr梯度的更新需要分y=1和y=0两种情况考虑：

(a) y=1时：此时表示有点击无转化


其中是原始ctr更新的梯度。但是因为考虑到ivr的loss，会在原来ctr的梯度反方向上加上(ivr的几率)倍的ctr更新梯度。
直观含义为：

即便一条样本被点击了，但是由于最终没有转化，随着ivr几率的大小，ctr模型的更新需要向反方向进行调整，在极端情况下，即ivr几率大于1，ctr的梯度反向更新；这样的修正是符合直觉的，没有转化的ctr的正样本的置信度小于有转化的正样本的置信度；

(b) y=0时：此时表示无点击也无转化


其中是原始ctr更新的梯度。如y=1情况类似，由于考虑ivr的loss，引入修正项，其中与原始梯度方向相反。

5.FTRL optimizer

有了损失函数的梯度，我们就可以通过FTRL算法进行online learning。不过与传统的model train不同的地方在于：

FTRL的算法框架如下：
Alt text

使用FTRL优化的EESMM代码如下：
算法步骤如下：
(1) 解析训练样本，分别提取ctr和cvr特征，并进行特征组合
(2) 根据λ1更新每个feature的weight
(3) 根据更新后的weight分别预估ctr和cvr
(4) 根据预估的ctr和cvr，分别更新两个子任务的梯度和学习率等超参变量
(5) 继续(1)
(6) 保存ctr和cvr模型

private void optimize(Sample sample) {
    for (int i = 0; i < sample.strFeaturesCtr.size(); ++i) {
        for (int m = 0; m < modelConfig.paraSize(); ++m) {
            Parameter parameter = modelConfig.getPara(m);
            if (featureInfo.z[m] <= parameter.ctr_lambda1 && featureInfo.z[m] >= -parameter.ctr_lambda1) {
                featureInfo.omiga[m] = 0;
            } else {
                double rst = -1 / ((parameter.ctr_beta + sample.sqrtNCtr[i]) / parameter.ctr_alpha + parameter.ctr_lambda2)                         * (featureInfo.z[m] - Math.signum(featureInfo.z[m]) * parameter.ctr_lambda1);
                featureInfo.omiga[m] = rst;
            }
        }
    }
    for (int i = 0; i < sample.strFeaturesCvr.size(); ++i) {
        for (int m = 0; m < modelConfig.paraSize(); ++m) {
            Parameter parameter = modelConfig.getPara(m);
            if (featureInfo.z[m] <= parameter.cvr_lambda1 && featureInfo.z[m] >= -parameter.cvr_lambda1) {
                featureInfo.omiga[m] = 0;
            } else {
                double rst = -1 / ((parameter.cvr_beta + sample.sqrtNCvr[i]) / parameter.cvr_alpha + parameter.cvr_lambda2) * (featureInfo.z[m] - Math.signum(featureInfo.z[m]) * parameter.cvr_lambda1);
                featureInfo.omiga[m] = rst;
            }
        }
    }
    //calcuate gradient of loss(grad)
    predict(sample, predictCtr, null, grad, sample.featureInfosCtr, false, true);
    predict(sample, predictCvr, null, grad, sample.featureInfosCvr, false, false);

    // ctr feature update
    for (int i = 0; i < sample.featureInfosCtr.length; ++i) {
        FeatureInfo featureInfo = sample.featureInfosCtr[i];
        if (featureInfo == null) {
            continue;
        }
        for (int j = 0; j < modelConfig.paraSize(); ++j) {
            grad[j] = (sample.labelCvr - predictCtr[j]*predictCvr[j])*(1.0 - predictCtr[j])
                    / Math.max((1.0 - predictCtr[j]*predictCvr[j]), 0.001) + sample.labelCtr - predictCtr[j];
            grad[j] *= -1;
            delta[j] = (doubleSqrt(sample.nCtr[i] + grad[j] * grad[j]) - sample.sqrtNCtr[i]) / modelConfig.getPara(j).ctr_alpha;
            featureInfo.z[j] += grad[j] - delta[j] * featureInfo.omiga[j];
        }
        if (sample.labelCtr == 1) {
            featureInfo.positive += 1;
        } else {
            featureInfo.negtive += 1;
        }
    }
    // cvr feature update
    for (int i = 0; i < sample.featureInfosCvr.length; ++i) {
        FeatureInfo featureInfo = sample.featureInfosCvr[i];
        if (featureInfo == null) {
            continue;
        }
        for (int j = 0; j < modelConfig.paraSize(); ++j) {
            grad[j] = (sample.labelCvr - predictCtr[j]*predictCvr[j])*(1.0 - predictCvr[j])
                    / Math.max((1.0 - predictCtr[j]*predictCvr[j]), 0.001);
            grad[j] *= -1;
            delta[j] = (doubleSqrt(sample.nCvr[i] + grad[j] * grad[j]) - sample.sqrtNCvr[i]) / modelConfig.getPara(j).cvr_alpha;
            featureInfo.z[j] += grad[j] - delta[j] * featureInfo.omiga[j];
        }
        if (sample.labelCvr == 1) {
            featureInfo.positive += 1;
        } else {
            featureInfo.negtive += 1;
        }
    }
}

6.delay feedback问题

关于cvr预估的第三个重要问题“安装延迟"，这也是MindAlpha解决的一个重要难题。那么我们是如何解决的呢？
预知后事如何，且听下回分解......

7.致谢

Mobvista AI中心算法一哥——尹广学

参考文献

1 Entire Space Multi-Task Model: An Effective Approach for Estimating Post-Click Conversion Rate
2 Mobvista发布一站式全链路机器学习平台MindAlpha

添加新批注
在作者公开此批注前，只有你和作者可见。
回复批注