ICPC code (自用)(一版)

-

列表项

---

准备之后的版本把模板使用结构体封装，便于快速的调用以及综合。acm中由于利用结构体浪费的时间可以忽略不计。

一、基础算法

1 高精度

相比于OI，莫名其妙的，高精度在ACM/ICPC中相当常用，不知道是不是可以随意带入纸质资料和可以用自带高精度的语言编写代码的缘故

#include<stdio.h>
#include<string>
#include<string.h>
#include<iostream>
using namespace std;
//compare比较函数：相等返回0，大于返回1，小于返回-1
int compare(string str1,string str2)
{
    if(str1.length()>str2.length()) return 1;
    else if(str1.length()<str2.le*斜体文本*ngth())  return -1;
    else return str1.compare(str2);
}
//高精度加法
//只能是两个正数相加
string add(string str1,string str2)//高精度加法
{
    string str;
    int len1=str1.length();
    int len2=str2.length();
    //前面补0，弄成长度相同
    if(len1<len2)
    {
        for(int i=1;i<=len2-len1;i++)
           str1="0"+str1;
    }
    else
    {
        for(int i=1;i<=len1-len2;i++)
           str2="0"+str2;
    }
    len1=str1.length();
    int cf=0;
    int temp;
    for(int i=len1-1;i>=0;i--)
    {
        temp=str1[i]-'0'+str2[i]-'0'+cf;
        cf=temp/10;
        temp%=10;
        str=char(temp+'0')+str;
    }
    if(cf!=0)  str=char(cf+'0')+str;
    return str;
}
//高精度减法
//只能是两个正数相减，而且要大减小
string sub(string str1,string str2)//高精度减法
{
    string str;
    int tmp=str1.length()-str2.length();
    int cf=0;
    for(int i=str2.length()-1;i>=0;i--)
    {
        if(str1[tmp+i]<str2[i]+cf)
        {
            str=char(str1[tmp+i]-str2[i]-cf+'0'+10)+str;
            cf=1;
        }
        else
        {
            str=char(str1[tmp+i]-str2[i]-cf+'0')+str;
            cf=0;
        }
    }
    for(int i=tmp-1;i>=0;i--)
    {
        if(str1[i]-cf>='0')
        {
            str=char(str1[i]-cf)+str;
            cf=0;
        }
        else
        {
            str=char(str1[i]-cf+10)+str;
            cf=1;
        }
    }
    str.erase(0,str.find_first_not_of('0'));//去除结果中多余的前导0
    return str;
}
//高精度乘法
//只能是两个正数相乘
string mul(string str1,string str2)
{
    string str;
    int len1=str1.length();
    int len2=str2.length();
    string tempstr;
    for(int i=len2-1;i>=0;i--)
    {
        tempstr="";
        int temp=str2[i]-'0';
        int t=0;
        int cf=0;
        if(temp!=0)
        {
            for(int j=1;j<=len2-1-i;j++)
              tempstr+="0";
            for(int j=len1-1;j>=0;j--)
            {
                t=(temp*(str1[j]-'0')+cf)%10;
                cf=(temp*(str1[j]-'0')+cf)/10;
                tempstr=char(t+'0')+tempstr;
            }
            if(cf!=0) tempstr=char(cf+'0')+tempstr;
        }
        str=add(str,tempstr);
    }
    str.erase(0,str.find_first_not_of('0'));
    return str;
}
//高精度除法
//两个正数相除，商为quotient,余数为residue
//需要高精度减法和乘法
void div(string str1,string str2,string &quotient,string &residue)
{
    quotient=residue="";//清空
    if(str2=="0")//判断除数是否为0
    {
        quotient=residue="ERROR";
        return;
    }
    if(str1=="0")//判断被除数是否为0
    {
        quotient=residue="0";
        return;
    }
    int res=compare(str1,str2);
    if(res<0)
    {
        quotient="0";
        residue=str1;
        return;
    }
    else if(res==0)
    {
        quotient="1";
        residue="0";
        return;
    }
    else
    {
        int len1=str1.length();
        int len2=str2.length();
        string tempstr;
        tempstr.append(str1,0,len2-1);
        for(int i=len2-1;i<len1;i++)
        {
            tempstr=tempstr+str1[i];
            tempstr.erase(0,tempstr.find_first_not_of('0'));
            if(tempstr.empty())
              tempstr="0";
            for(char ch='9';ch>='0';ch--)//试商
            {
                string str,tmp;
                str=str+ch;
                tmp=mul(str2,str);
                if(compare(tmp,tempstr)<=0)//试商成功
                {
                    quotient=quotient+ch;
                    tempstr=sub(tempstr,tmp);
                    break;
                }
            }
        }
        residue=tempstr;
    }
    quotient.erase(0,quotient.find_first_not_of('0'));
    if(quotient.empty()) quotient="0";
}

2. 搜索

没啥好说的，代码不可能忘了。

3.贪心

更没啥好说的。

4.二分

题目分类

二分往往应用于求最大或者最小值，并且在判断一个值是否能够作为可行解的时候，有$O(n)$ 或者 $O(nlogn)$ 的方法可以判断。并且每一次的判断之间没有互相约束。

while (l<=r) 
    {
        int mid=(l+r)>>1;
        if (check(mid)) 
        {
            l=mid+1;
            ans=mid;
        } else r=mid-1;
    }

二、图论

1.最短路问题

最短路问题无疑是竞赛的热门考点，关于最短路有比较多的算法。

1.1 弗洛伊德

弗洛伊德算法支持邻接矩阵建图，并且在$O(n^3)$的时间复杂度找到任意两个点之间的最短路。由于方程的特殊性，往往可以支持除了最短路之外的其它的一些操作。

1.2 迪杰斯特拉算法

不带势的迪杰斯特拉算法无法处理带有负权边的问题。并且不使用堆优化的迪杰斯特拉时间复杂度相当高，很难在合适的时间内得出结果。还有一个，堆优化的迪杰斯特拉时间复杂度是$O(mlogn)$。

#include <bits/stdc++.h>
#define int long long 
using namespace std;
const int MAXN=2e5+7;
struct po
{
    int nxt,to,dis;
}edge[MAXN];
struct Node
{
    int dis,id;
    Node(){}
    Node(int dis,int id) : dis(dis), id(id){}
    bool operator < (const Node& rhs) const
    {
        return dis>rhs.dis;
    }
};
int dis[MAXN],b[MAXN],head[MAXN],num,n,m,s;
inline void add_edge(int from,int to,int dis)
{
    edge[++num].nxt=head[from];
    edge[num].to=to;
    edge[num].dis=dis;
    head[from]=num;
}
void Dijkstra(int s)
{
    memset(dis,100,sizeof(dis));
    priority_queue<Node> q;
    dis[s]=0;
    q.push(Node(0,s));
    while(!q.empty()){
        Node u=q.top();q.pop();
        if(b[u.id]) continue;
        b[u.id]=1;
        for(int i=head[u.id];i;i=edge[i].nxt){
            int v=edge[i].to;
            if(dis[v]>u.dis+edge[i].dis){
                dis[v]=u.dis+edge[i].dis;
                q.push(Node(dis[v],v));
            }
        }
    }
}
main()
{
    cin>>n>>m>>s;
    for(int i=1;i<=m;i++){
        int u,v,l;
        cin>>u>>v>>l;
        add_edge(u,v,l);
    }
    Dijkstra(s);
    for(int i=1;i<=n;i++) cout<<dis[i]<<" ";
    return 0;
}

1.3 SPFA

这算法虽然死了，但是如果不刻意去卡，往往能够拥有比迪杰斯特拉更好的时间效率，并且可以轻松的支持负权边，还能同时找出负环，是有它自己的作用的。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<queue>
#define re register
#define ll long long 
#define MAXN 200005
using namespace std;
struct po{
    int nxt,to,dis;
};
po edge[MAXN];
int b[MAXN],dis[MAXN],n,m,s,t,head[MAXN],num;
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch>'9'||ch<'0')&&ch!='-')ch=getchar();
    while(ch=='-')c*=-1,ch=getchar();
    while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
inline void add_edge(int from,int to,int dis)
{
    edge[++num].nxt=head[from];
    edge[num].to=to;
    edge[num].dis=dis;
    head[from]=num;
}
inline void spfa()
{
    memset(dis,50,sizeof(dis));
    queue<int> q;
    dis[s]=0;
    b[s]=1;
    q.push(s);
    while(!q.empty()){
        int u=q.front();
        q.pop();
        b[u]=0;
        for(re int i=head[u];i;i=edge[i].nxt){
            int v=edge[i].to;
            if(dis[v]>dis[u]+edge[i].dis){
                dis[v]=dis[u]+edge[i].dis;
                if(!b[v]){
                    b[v]=1;
                    q.push(v);
                }
            }
        }
    }
}
int main()
{
    n=read();m=read();s=read();
    for(re int i=1;i<=m;i++){
        int x,y,l;
        x=read();y=read();l=read();
        add_edge(x,y,l);
    }
    spfa();
    for(re int i=1;i<=n;i++){
        printf("%d ",dis[i]);
    }
}

对于负环类的问题，只需要判断一个点的入队次数是否大于n即可。

2.缩点（Tarjan）

缩点往往是可以重复经过某些点但是每条边的贡献只有一次的时候会单独使用，其他时候更多会以某种算法的辅助而存在。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXN=2e5+7;
struct po
{
    int nxt,from,to;
    po(){}
    po(int nxt,int from,int to):nxt(nxt),from(from),to(to) {}
}edge[MAXN],Edge[MAXN];
int head[MAXN],dfn[MAXN],low[MAXN],dis[MAXN],a[MAXN],stacok[MAXN],val[MAXN];
int Head[MAXN],b[MAXN],cnt,color_num,col[MAXN],vis[MAXN],num,nm,tp,s,t,n,m;
inline int read()
{
    int x=0,c=1;char ch=' ';
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    while(ch=='-') c*=-1,ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return x*c;
}
void Tarjan(int u)
{
    dfn[u]=low[u]=++cnt;
    stacok[++tp]=u; vis[u]=1;
    for(int i=head[u];i;i=edge[i].nxt){
        int v=edge[i].to;
        if(!dfn[v]){
            Tarjan(v);
            low[u]=min(low[u],low[v]);
        } else if(vis[v]) low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u]){
        color_num++;
        col[u]=color_num;
        vis[u]=0;
        while(stacok[tp]!=u){
            col[stacok[tp]]=color_num;
            val[color_num]+=a[stacok[tp]];
            a[stacok[tp]]=0;
            vis[stacok[tp--]]=0;
        }
        tp--;
    }
}
void spfa()
{
    memset(dis,0,sizeof(dis));
    b[s]=1;
    queue<int> q;
    q.push(s);
    while(!q.empty()){
        int u=q.front();q.pop();
        b[u]=0;
        for(int i=Head[u];i;i=Edge[i].nxt){
            int v=Edge[i].to;
            if(dis[v]<dis[u]+val[v]){
                dis[v]=dis[u]+val[v];
                if(!b[v]){
                    q.push(v);
                    b[v]=1;
                }
            }
        }
    }
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++){
        a[i]=read();
    }
    for(int i=1;i<=m;i++){
        int u,v;
        u=read();v=read();
        edge[++num]=(po(head[u],u,v));
        head[u]=num;
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i]) Tarjan(i);
    for(int i=1;i<=m;i++){
        int u=edge[i].from,v=edge[i].to;
        val[col[u]]+=a[u];
        val[col[v]]+=a[v];
        a[u]=a[v]=0;
        if(col[u]!=col[v]){
            Edge[++nm]=po(Head[col[u]],col[u],col[v]);
            Head[col[u]]=nm;
        }
    }
    s=0,t=color_num+1;
    for(int i=1;i<=color_num;i++){
        Edge[++nm]=(po(Head[s],s,i)); Head[s]=nm;
        Edge[++nm]=(po(Head[i],i,t)); Head[i]=nm;
    }
    spfa();
    cout<<dis[t];
}

3.双连通分量

对于一个连通图，如果任意两点至少存在两条点不重复路径，则称这个图为点双连通的（简称双连通）；如果任意两点至少存在两条边不重复路径，则称该图为边双连通的。点双连通图的定义等价于任意两条边都同在一个简单环中，而边双连通图的定义等价于任意一条边至少在一个简单环中。对一个无向图，点双连通的极大子图称为点双连通分量（简称双连通分量），边双连通的极大子图称为边双连通分量。

3.1 边双连通分量

一个边双连通分量中，内部无桥

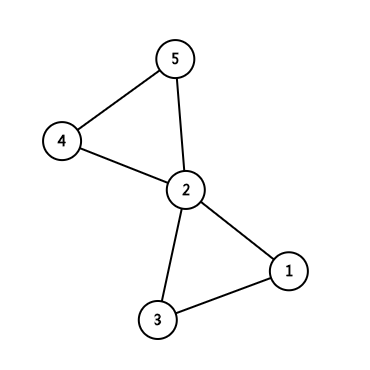
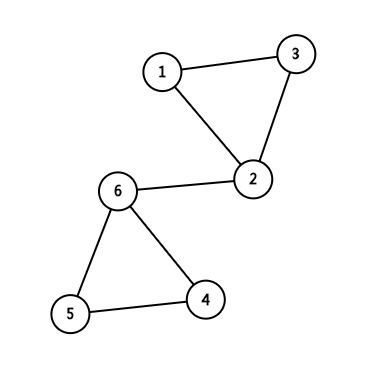
第一张图中五个点在同一个边双连通分量中，第二张图中，边$<2,6>$是桥，将两个边双连通分量连通。

边双连通分量处理过后可以得到一棵树，可以通用树形的各种算法。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXN=1e5+7;
struct po
{
    int u,v;
    po(){}
    po(int u,int v):u(u),v(v){}
}e[MAXN];
int dfn[MAXN],low[MAXN],bridge[MAXN],bccno[MAXN],cnt,bcc_cnt,n,m,num=-1;
vector<int> edge[MAXN];
void Tarjan(int u,int fa)
{
    dfn[u]=low[u]=++cnt;
    for(int i=0;i<edge[u].size();i++){
        int v=e[edge[u][i]].v;
        if(!dfn[v]){
            Tarjan(v,u);
            low[u]=min(low[v],low[u]);
            if(low[v]>dfn[u]){
                bridge[edge[u][i]]=1;bridge[edge[u][i]^1]=1;
            }
        } else if(dfn[v]<dfn[u]&&v!=fa){
            low[u]=min(low[u],dfn[v]);
        }
    }
}
void dfs(int u)
{
    dfn[u]=1;bccno[u]=bcc_cnt;
    for(int i=0;i<edge[u].size();i++){
        int v=e[edge[u][i]].v;
        if(bridge[edge[u][i]]) continue;
        if(!dfn[v]) dfs(v);
    }
}
void find_ebcc()
{
    for(int i=1;i<=n;i++) if(!dfn[i]) Tarjan(i,-1);
    memset(dfn,0,sizeof(dfn));
    for(int i=1;i<=n;i++){
        bcc_cnt++;
        if(!dfn[i]) dfs(i);
    }
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int u,v;
        cin>>u>>v;
        e[++num].u=u;e[++num].v=v;
        edge[u].push_back(num);
        e[++num].u=v;e[++num].v=u;
        edge[v].push_back(num);
    }
    find_ebcc();
    for(int i=1;i<=n;i++) cout<<bccno[i]<<" ";
}

3.2 点双连通分量

(1).点双连通分量之间以割点连接，且两个点双连通分量之间有且只有一个割点。
证明：
若两个点双连通分量之间共用两个点，则删除其中任意一个点，所有点依旧连通。
如图：

​

(2).每一个割点可任意属于多个点双连通分量，因此求点双连通分量时，可能包含重复的点。
(3).只有一条边连通的两个点也是一个点双连通分量，如：

​

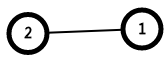
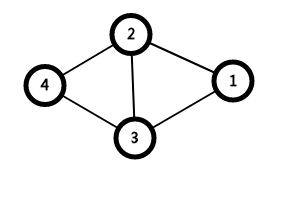
​ 所以，在下图中，存在（1、2、3）,（3、4），（4、5、6）三个点双连通分量。

​

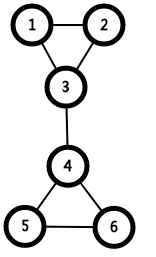
(4).对于此点为根的情况，第一个儿子也属于点双连通分量，故不能用判断割点的方法来判断，

​ 只要dfn[父]<=low[子]，便可将其加入点双：

​

​ 在此图中，1、2、3、4在同一个点双连通分量里，但2是1的第一个儿子

(5).对于删去此点不会不与祖辈连通的儿子，在处理其他儿子的点双连通分量时，不能将其删去，如。

​

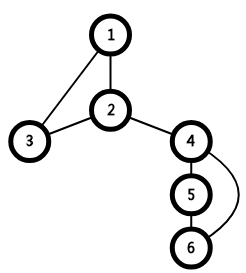
​ 1、2、3共同构成一个点双连通分量，不能在处理4、5、6是将其删去。

​ 所以代码不该为：

​

         while(s[top]!=u) ++siz[tot]=s[top],num[s[top]]=tot,--top;

​ 而应是

​

        v=e[i].to;
        while(s[top+1]!=v) ++siz[tot],num[s[top]]=tot,--top;

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int MAXN=1e5+7;
struct po
{
    int u,v;
    po(){}
    po(int u,int v):u(u),v(v){}
}e[MAXN];
int n,m,dfn[MAXN],low[MAXN],iscut[MAXN],bccno[MAXN],cnt,nm;
int tp,stackk[MAXN],bcc_cnt;
vector<int> edge[MAXN],bcc[MAXN];
void Tarjan(int u,int fa)
{
    int child=0;
    dfn[u]=low[u]=++cnt;
    for(int i=0;i<edge[u].size();i++){
        int v=e[edge[u][i]].v;
        if(!dfn[v]){
            stackk[++tp]=edge[u][i],child++;
            Tarjan(v,u);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]){
                iscut[u]=1;
                bcc[++bcc_cnt].clear();
                while(1){
                    int num=stackk[tp--];
                    if(bccno[e[num].u]!=bcc_cnt){
                        bcc[bcc_cnt].push_back(e[num].u);
                        bccno[e[num].u]=bcc_cnt;
                    }
                    if(bccno[e[num].v]!=bcc_cnt){
                        bcc[bcc_cnt].push_back(e[num].v);
                        bccno[e[num].v]=bcc_cnt;
                    }
                    if(e[num].u==u&&e[num].v==v) break;
                }
            }
        } else if(dfn[v]<dfn[u]&&v!=fa) {
            stackk[++tp]=edge[u][i];
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(fa<0&&child==1) iscut[u]=0;
}
void find_bcc()
{
    for(int i=1;i<=n;i++) if(!dfn[i]) Tarjan(i,-1);
}
inline int read()
{
    int x=0,c=1;char ch=' ';
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    while(ch=='-') c*=-1,ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return x*c;
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=m;i++){
        int u,v;
        u=read();v=read();
        e[++nm]=po(u,v);
        edge[u].push_back(nm);
        e[++nm]=po(v,u);
        edge[v].push_back(nm);
    }
    find_bcc();
    for(int i=1;i<=n;i++){
        if(iscut[i])
            cout<<i<<" ";
    }
    cout<<endl;
    for(int i=1;i<=bcc_cnt;i++){
        cout<<bcc[i].size()<<" ";
    }
}

对拍用的模板，可以参考。

#include <bits/stdc++.h>
using namespace std;
const int maxn = 110;
const int maxm = 10010;
struct node
{
    int u, v, next;
}edge[maxm], tp;
int n, m;   //点数，边数 
int head[maxn], no;
int add_bcc[maxn];//去掉该点之后能增加的bcc数目
int index; //时间戳 
int yltd;   //图的初始连通分量 
int num[maxn], low[maxn];//时间戳和能回到的最早时间戳 
int iscut[maxn];//是否为割点 
int bccno[maxn], bcc_cnt; //bccno[i]表示i属于哪个bcc 
stack<node> S;  //存储bcc边 
vector<int> bcc[maxn];
inline void init()
{
    no = 0;
    memset(head, -1, sizeof head);
}
inline void add(int u, int v)
{
    edge[no].u = u; edge[no].v = v;
    edge[no].next = head[u]; head[u] = no++;
    edge[no].u = v; edge[no].v = u;
    edge[no].next = head[v]; head[v] = no++;
}
inline void input()
{
    int u, v;
    for(int i = 1; i <= m; ++i)
    {
        scanf("%d %d", &u, &v);
        add(u, v);
    }
}
void tarjan(int cur, int father)
{
    int child = 0;
    num[cur] = low[cur] = ++index;
    int k = head[cur];
    while(k != -1)
    {
        int v = edge[k].v; 
        if(!num[v])
        {
            S.push(edge[k]);
            ++child;
            tarjan(v, cur);
            low[cur] = min(low[cur], low[v]);
            if(low[v] >= num[cur])  
            //把更节点看做普通的节点，对根节点这个条件是一定满足的，
            //可以实现把回溯到根节点剩下的出栈，其实这就是一个新的双连通分量 
            {
                iscut[cur] = 1;
                ++add_bcc[cur];
                ++bcc_cnt;//准备把新的双连通分量加入bcc 
                bcc[bcc_cnt].clear();
                while(true)
                {
                    tp = S.top(); S.pop();
                    if(bccno[tp.u] != bcc_cnt)
                    {
                        bcc[bcc_cnt].push_back(tp.u);
                        bccno[tp.u] = bcc_cnt;
                    }
                    if(bccno[tp.v] != bcc_cnt)
                    {
                        bcc[bcc_cnt].push_back(tp.v);
                        bccno[tp.v] = bcc_cnt;
                    }
                    if(tp.u == edge[k].u && tp.v == edge[k].v) break;
                }
            }
        }
        else if(num[v] < num[cur] && edge[k].v != father)
        {
            //num[v] < num[cur]的判断是为了防止当前cur为割点，然后它刚访问的一个双连通分量里有一个较深的点
            //访问过了。然后再从cur访问，如果不判断就会将这个点加入S，造成错误，见上图。 
            //可以看到时间戳走到6再次回溯到2时，还能通过2对2-4这条边进行一次尝试，不判断的话4会被加到S
            S.push(edge[k]);
            low[cur] = min(low[cur], num[v]);
        }
        k = edge[k].next;
    }
    if(father < 0)
    {
        //把根节点看做普通节点了，所以下面最后的特殊判断必需。 
        if(child > 1) iscut[cur] = 1, add_bcc[cur] = child-1;
        else iscut[cur] = 0, add_bcc[cur] = 0;
    }
}
void Find_Cut(int l, int r)
{
    index = bcc_cnt = yltd = 0;
    memset(add_bcc, 0, sizeof add_bcc);
    memset(num, 0, sizeof num);
    memset(iscut, 0, sizeof iscut);
    memset(bccno, 0, sizeof bccno);
    memset(low, 0, sizeof low);
    for(int i = l; i <= r; ++i)
    {
        if(!num[i]) tarjan(i, -1), ++yltd;
    }
}
void PutAll(int l, int r)
{
    for(int i = l; i <= r; ++i)
    {
        if(iscut[i]) printf("%d是割点，", i);
        printf("去掉点%d之后有%d个双连通分量\n", i, add_bcc[i]+yltd);
    }
}
void PutBcc()
{
    printf("有%d个BCC\n", bcc_cnt);
    for(int i = 1; i <= bcc_cnt; ++i)
    {
        printf("BCC%d有%d个点: ", i, bcc[i].size());  
        for(int j = 0; j < bcc[i].size(); ++j) printf("%d ", bcc[i][j]);  
        printf("\n");  
    }
}
int main()
{
    while(~scanf("%d %d", &n, &m))
    {
        init();
        input();
        Find_Cut(1, n);
        PutAll(1, n);
        PutBcc();
    } 
    return 0;
}

4.网络流

网络流算图论吧，应该算吧。

使用建模基础概括一下得了。

此部分会有目录紊乱问题，我也懒得改了。

网络流建模方法一览

大锅博主终于找回来了原稿。。。。

哈，据说加上最详细这几个字会比较容易吸引人阅读。

资料来源：百度百科（笑~

    还有一些dalao的博客，不过也都只是因为不想打字了就copy一些很通俗的结论过来，全文几乎都是笔者的原创。

注：此文随着笔者的不断做题持续更新。

已经很熟悉网络流的dalao可以从七开始看，或许能有些收获。

网络流的题目，大部分都是在考建模，很少有考你板子的。。。除非你非得用EK结果被卡上天。笔者从做过的所有网络流的题目里寻找了一些比较常用和经典的建模方式，一共大家学习。

那么就从简单到难一步步看吧。

一、傻逼建图法

笔者打上这两个字是绝对没有任何问题的，让我们来想想网络流的模板题的要求是什么。

（注：笔者选取了洛谷为题目来源，原因竟是视觉效果友好）

很明显， 没有比这种题目更简单的网络流了，题目给你怎么连的边，你就照着题目连上就可以了，几乎是把你当做一个啥都不会的人手把手教你建图。。但是这种题目的数据范围一般较大，建议使用较高效率的网络流算法。

二、超级源点和汇点的设置

这应该是网络流题目中最最最最常用的一种方法了。经常有题目，我们要求一些最小的利益什么的，但是明显没有可用的源点和汇点或者更多情况是题目中给出了不止一个源点和汇点，这时候就要建立超级源和超级汇，把所有的题目中的可行源点和汇点分别连接到超级源和超级汇上，而事实上，我们拿到任何一道网络流题目，除非它的源点和汇点是严格给定的，我们都可以尝试建立超级源汇从而达到减小建模难度的目的。

例题：飞行员匹配问题

题解：这个题我们先不管输出方案，只看要输出的那个最大值，很明显，如果我们把英国飞行员当成源点，外国飞行员当成汇点的话，会有很多源点和汇点，本着方便至上的原则，建立超级源汇，然后板子即可。
前面的题目这么简单笔者并不想放代码

三、最小割类问题

这其实是一个很关键的定理。事实上真要细细的说这个总结里写的肯定是不够用的。我们在做题的时候，有时会遇到这样的一类问题，就是给你一个图，然后给你边权，问你如何在割掉的边权尽量小的情况下把指定的两个点or两个集合分开。然后我们就把你求得的这个最小的边权和叫做这个图的最小割。

那么补上之前不想证明的结论。

首先最大流==最小割

为什么呢，想象一下，我们现在有这么一个有向图，然后，最大流是小于等于割的，那么。。。在最大流=某个割的时候这个割就是最小的。。。感性理解一下的话，一个最大流跑到那个图上，这个图怎么看S也没法连到T去了。

然后最小割的唯一性？

我们考虑一条边是否一定在最小割中。明显，我们跑完一遍网络流之后残量网络里满流的边都是可能在最小割里的，然后又到了跑Tarjan的时候了，如果这条边在最小割里，那么跑完Tarjan之后它所连接的两个端点一定是在不同的强连通分量里。如果是的话，用脑子想想，割了这条边这个图还是没分开啊。

那么我们也可以由此得证，假设一条边所连接的点一个在S所在的强连通分量里，一个在T所在的强连通分量里的话，那么这条边一定在最小割里。

1.平面图最小割=最大流=对偶图最短路

然后就是转换成对偶图的最短路的问题。其实这已经不应该算在网络流的范畴里了（因为它变成了最短路）。那么就不在这里详述了，具体的可以去看看[BZOJ1001]狼抓兔子，虽然可以最大流全力优化蜜汁跑过。

我们在这里还是讨论最小割的问题

2.割边

这种就是我们所说的最平常的最小割问题，我们只需要直接求出图的最大流就可以了。

然后是一些高深一些的建模：有很多题目都会让你求这样一个东西，就是怎么安排这些balabala的工作可以获得balabala的利益，然后让你去求这个最大利益。很多人都会正常的去想最大流的做法但是由于有限制条件，所以不能像那么求。然后我们不妨转换一下，如果我们所有的都可以选，我们是不是可以得到一个最大利益，然后我们考虑的是放弃最小的利益和，这样我们就把这个题转换成了一个最小割的问题，可以利用最大流求出。

然后随之而来的就是另一个模型：最大权闭合图。这类题目都可以转化为最小割来求解，具体证明还是请百度吧，这篇文章并不是介绍这类东西的，并且笔者对这些模型的证明也不如网上的神犇。现在笔者又回来证这个东西了。请向后翻阅，自然能找到。。

例题：Luogu P3410 拍照

题解：这题就是一个最大权闭合图的模型，求出总利益减去不可得的利益就可以了，连边的话比较容易就不详述了，不过再往后的题目应该就会有连边的思路了。毕竟前面这些都是些入门题目。

例题：方格取数问题

题解：我们可能会有一个比较基础的贪心思想，没错，就是隔一个取一个，但是这么做并不可行，具体反例很容易找。然后我们通过观察，发现这道题和某最大权闭合子图有些类似，如果我们全取所有点，删去最小割说不准可行。 开始考虑建图，首先所有的奇数格子连源点，偶数格子连汇点，边权为点权。他们之间的边只连奇数到偶数的，边权为inf，这么连是为了避免重复计算。然后直接DINIC最大流就可以了。

3.割点(?)

这也是最小割的一种经典问题，具体实现方式我们等下放在拆点那个栏目里讲，这里就先不说了。

四、拆点

说实话，网络流最难思考的地方就在这里了，几乎所有拿得出来的经典的题目都是神奇的拆点然后求出最大流。

1.基础拆点——入点和出点

经常有这一类问题，一个图给出了点权而不是边权，我们在连接边的时候就显得十分不好操作，这个时候我们往往就会有这样一种操作，把每个点拆成入点和出点，题目给出的连边均由每个点的出点连向入点，然后每个点的入点和出点之间连一条流量为点权的边，就可以满足点权的限制了。

然后让我把刚才的坑补一下：割点

我们在很多时候都会发现，在求最小割的时候，我们要割的不是边，而是割掉一个点。这时候我们再用刚才的直接跑的方法很明显就不可以了。因为割掉一条边最多只影响两个点之间的连边，而割掉了一个点的话，与这个点相连的所有边就都失去了作用。这个时候我们就可以先拆点，然后把这个点入点和出点之间的那条边割掉，就相当于是这个点在图中不存在了。

例题：教辅的组成

题解：本题的构图思路可以表示为：
源点->练习册->书(拆点)->答案->汇点
注意一定要拆点，因为一本书只能用一次。
由于题目难度不大，这个题就提点到这里了。

例题：奶牛的电信

为什么找这道奶牛题。。以为确实是割点的题目不是很好找，剩下的题目不大适合放在这个地方。如果你好好看了刚才的割点，这个题应该可以直接做出来了。不详述了。

2.按照时间拆点

有一部分题目是这样的，我们给出的图的同时也给出了一个天数或者时间的限制，然后对每一天做出询问，最后求总和，很明显的一点是，要把每一天都连向汇点然后求出总和。这个时候我们发现，如果其他的点仅仅只是一个点的话，无法满足求出每一天这个要求，因为会互相影响，这个时候我们就相应的把这些点拆成天数这么多个点，然后分别向向对应的天数连边。例题的话一会会有一些笔者认为比较好的题集中放在一起，这里就先介绍建图方法了。

3.根据时间段拆点

这不是和上面那个一样么？？？实际上不是的，注意，刚才那个是时间，而这个是时间段。不过说实话这种拆点方式主要是在费用流里出现，因为有很多这种题目，就是一个人在不同的流量是费用是不一样的，所以为了满足这个要求，就把这个人拆成一共有多少不同费用的点。举个例子：你们数学老师今天布置作业越多，你的不满值越大，如果是5张以下，一张卷子增加1点不满值，如果10张以下，一张卷子增加两点，如果10张以上，那么一张卷子增加inf点不满值。那么我们就把你拆成三个点，分别对应三种不满值。

4.蛇皮拆点

有很多题目，拆点往往十分难想或者蛇皮至极有很多典型的例子就不一一详述了，比如什么一个点拆三个点四个点之类的。直接说一些例题貌似是比较好的。

[CQOI2012]交换棋子

这题不建议刚学费用流的人做，因为确实比较恶心，容易打击到自己。首先，我们可以发现交换这个操作是很难去用流量描述和限制的。那我们应该怎么办？如果我们把格子上的所有黑棋子当棋子，而剩下的白子就当成空的格子，我们就把一个交换的操作当成了一个移动的操作。那么如何限制流量呢？我们这个题要求的是每个格子参与交换的次数，针对一次交换要使用两个格子的次数，我们把格子拆成入点，原点和出点，分别计算，至于交换次数自然让费用承担。好了，这只是大体的思路，但是实际上这题还有很多坑点和不好理解的地方。

拆点更多的是一种工具，而且是网络流里必要和强大的工具。能不能想出拆点的方法从而跑出网络流，往往是解决网络流问题的关键。

五、枚举和二分

原先这个版块叫枚举而二分最大流量，现在想想，当时的理解还是不够深刻，实际上，能够枚举和二分的远远不止流量。这里详细重新讲述一下。

1.枚举和二分流量条件

当然，这个部分依然是必不可少的。

有这样一部分题目，它给你的图不一定是完整的，往往需要你确定一个值来确定是否能够跑出期望的最大流。就比如说去计算一个最少的时间或者花费时，我们并没有一个具体的数值，这个时候我们往往预先通过连接inf先跑一遍最大流，之后二分时间每次重构图，再次跑最大流，并且通过此时的流量是否和刚才相等来调整二分的上下界。抑或跟人数有关的题目，我们二分的时候判断最大流是否等于当前人数。

然后枚举的建图方法就更是简单，每次枚举+1时重构图，然后一直跑到不能再跑了为止。

2.枚举和二分费用

费用流的题目中，有些题目会给你费用的限制，或者说是间接的控制了你的流量，比如说他要一个满足条件时可能的最小费用，你仍然可以像刚才二分流量时那么跑。但是它也有可能要一个不超过一个费用时能满足的最大条件，这个时候去二分那个条件，然后控制费用。

3.枚举和二分边和点

有的题目里，各个点的添加是有顺序的，每个点的边的添加也可能是有顺序的，这个时候就有一类问题会让你确定一个值，要这个值之前的所有点可以满足最大流量，这个时候我们就要二分加入图中的点了，边也是同理。不过总的来说，二分的方法万变不离其宗，总是要通过流量或者费用调整二分上下界。

六、点的构造

大部分题目是有迹可循的，因为他们至少有点或者有明显能够当做点的状态。或者题目给出的点就真的能够当成点使用。但是也有的题目，并没有明显的点的提示，或者给出的你明显的点完全不能够当成网络流里的点使用。对于这种题目，我们就要自己构造出来一些新的点来进行网络流的使用。
单说可能不是很好理解，我们放上几道题给大家看一下。

[HEOI2016/TJOI2016]游戏

这道题目大意就是让我们在一个矩阵里放东西，如果没有硬石头限制，就是同行同列只能放一个。然后考虑算法，n,m<=50很明显这题与什么数据结构啊什么的是没有缘分了。那么就是DP或者网络流了。。考虑DP明显的状态太多根本没法转移，那么网络流呢？这一个一个点完全没有什么用处连起来也没法限制。。。这时候我们就要对这些已经有的点进行重构，根据网络流能够描述互斥关系的原理来搞出这道题。
那么：
这张网格图可以抽象成一系列行块和列块，列块和行块就是说,这一个横行块或纵列块里至多放一个炸弹，另外显而易见的,我们发现选中一个点的时候会同时选中两个块，那么也就是说这张图满足两个限制条件
1.每个点最多被选中一次
2.某些点对之间有必选关系
那么之后连边跑网络流即可了。

BZOJ4950:[Wf2017]Mission Improbable

先说一下题目大意，就是有一个网格方阵，每个格子里都有一个权值，题目要求你在保证每行每列最大的权值不变的情况下，取走尽量多的权值。并且本来有权的格子里不能取成0。

不取成0不用考虑，留下1就可以了。那么剩下的就是保证每行每列最大值不变了。我们可以贪心的考虑每行都把那个最大的留下，如果有那么一行一列的箱子的最大值是相同的，这个时候把最大值放在交点处很明显就要比放在其它的地方要好的多。那么怎么处理这种情况呢？可以像上面的题目那样把每行每列都构造成点，然后一旦出现了刚才那种点，就连起来。之后跑一遍最大流，就可以求出来我们能够放在交点出的最大值是多少了。

七、动态思想

1.基本介绍

有一些题目是这个样子的，他们往往有着较其他网络流题目更大的数据，并且他们也有一个特点，就是在一部分边连好之后，之后是先建建图或者是跑一个点再加一个点这么建图对最终结果并没有影响。这样一来我们就可以通过动态加点或者边的方式使其满足题目要求的复杂度。

2.限制条件

2.1数据范围不能过大

虽说是减小了时间复杂度，但是也只是减少了部分，很多情况下复杂度的等级并没有变化，只是因为在大部分操作里减少了一些不必要的操作使速度加快。

2.2主要应用于费用流

大多时候动态加点的题目都是费用流题目，原因就是最短路一次基本上也就只能增广出来一条增广路，如果是网络流的话，当前弧优化往往能够取到更好的效果。费用流由于大部分人都会使用EK的朴素算法，所以动态加点可以是速度提高好几个档次。

2.3当前最优原则

刚才说过了前面点的选择不会影响后面的选择，这里仔细说一下。因为在跑网络流的时候，不可避免的后面跑的点回合前面跑的点有冲突，这个时候我们可以通过反边来使冲突化解。那么如果我们一个一个的加点，很明显就没办法满足这个条件。但是如果我们可以确定当前这个点跑了这个流，后面的点跑这个流的一定不如这个点优，那么我们就可以无视那个冲突了。

3.经典的例子

对于这个思想有一个很经典的题目，更好的是它甚至有数据弱化版来对比。

[NOI2012]美食节&&[SCOI2007]修车

这两个题的原理都是一样的，就是差在了一个数据范围，我们先说后面那个数据范围小的。

题目描述

同一时刻有N位车主带着他们的爱车来到了汽车维修中心。维修中心共有M位技术人员，不同的技术人员对不同的车进行维修所用的时间是不同的。现在需要安排这M位技术人员所维修的车及顺序，使得顾客平均等待的时间最小。

说明：顾客的等待时间是指从他把车送至维修中心到维修完毕所用的时间。

数据范围

(2<=M<=9,1<=N<=60), (1<=T<=1000)

Solution

要求平均时间最短，就等同于要求总时间最短

对于一个修车工先后用$W_1-W_n$的几个人，花费的总时间是

$$W_n\times 1+W_{n-1} \times 2+...+W_1 \times n$$

不难发现倒数第a个修就对总时间产生a*原时间的贡献

然后我们将每个工人划分成N个阶段，(i,t)表示修车工i在倒数第t个修

可以建一个二分图，左边表示要修理的东西，右边表示工人+阶段

于是可以从左边的e向右边的(i,t)连边，权值是$Time[e][i]*t$，就是第e个用i这个修车工所用时间

最小权值完全匹配后，最小权值和除以N就是答案

因为权值是正的，所以一个修车工接到的连线一定是从(i,1)开始连续的，也符合现实情况

因为假设是断续的，那后面的(i,n)改连向(i,n-k),k

这样我们建立好图以后直接跑费用流就可以了。

那么我们继续看下一道题

题目描述 2.0

m个厨师都会制作全部的n种菜品，但对于同一菜品，不同厨师的制作时间未必相同。他将菜品用1, 2, ..., n依次编号，厨师用1, 2, ..., m依次编号，将第j个厨师制作第i种菜品的时间记为 ti,j 。小M认为：每个同学的等待时间为所有厨师开始做菜起，到自己那份菜品完成为止的时间总长度。换句话说，如果一个同学点的菜是某个厨师做的第k道菜，则他的等待时间就是这个厨师制作前k道菜的时间之和。而总等待时间为所有同学的等待时间之和。现在，小M找到了所有同学的点菜信息: 有 pi 个同学点了第i种菜品（i=1, 2, ..., n）。他想知道的是最小的总等待时间是多少。

数据范围 2.0

对于100%的数据，n <= 40, m <= 100, p <= 800, ti,j <= 1000 （其中p = ∑pi）

Solution 2.0

连边还是和上一个题目一样。那么数据范围变大了，我们现在的时间复杂度就是O（$n^2m\times p \times \overline k$）嗯，T了。

那么怎么办呢？通过仔细的思考可以发现，我们观察发现，第一次spfa得出的最短路肯定是某人倒数第一个修某车某厨师倒数第一个做某菜，因为倒数第一个肯定比倒数第二个距离短

那么我们可以在一开始建图的时候，只把所有“倒数第一个做的菜”的那些边加上

一旦一条增广路被用掉了（也就是一个厨师-做菜顺序二元组(j,k) 被用掉了），那么我们就把所有代表二元组(j,k+1) 加上去（一共有n条），再跑spfa

这样我们图中的总边数不会超过$n\ast\sum_{i=1}^n p \lbrack i\rbrack$

也就是总时间在$O\left(np^2\ast \overline k\right)$左右，k是spfa常数，就可以通过这道题。

八、二分图

二分图又称作二部图，是图论中的一种特殊模型。 设G=(V,E)是一个无向图，如果顶点V可分割为两个互不相交的子集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为一个二分图。

好了不介绍这东西的基本定义了随便百度百度就应该能百度到了，至于增广路什么的也都去看看基础教程吧，笔者这里说的是网络流的建模。。

1.最大匹配

众所周知（？），二分图的最大匹配就是在二分图上跑出来的最大流。那么最优匹配什么的也可以网络流搞搞搞出来，而且时间复杂度一般都要比想象的好很多，大部分比匈牙利要快。。。

2.基本定义

为了方便待会理解，这里特别放上几个基本的定义。

最小覆盖：即在所有顶点中选择最少的顶点来覆盖所有的边。

最大匹配：二分图左右两个点集中，选择有边相连的两个匹配成一对（每个点只能匹配一次），所能达到的最大匹配数。

独立集：集合中的任何两个点都不直接相连。

3.最小覆盖数=最大匹配数

这个比较基础，证起来主要看自己理解吧，具体的证明我也没有特别好的思路，不过还是尽量给大家证一下吧。我们先搞一个二分图，然后最大匹配一下，如图，绿点就是匹配成功的点，红点就是匹配失败的点。那么我们可以发现，每一条边都有两种情况，一种是连了一个红点一个绿点，一种是连了两个绿点。可以发现，没有任何一条边会连接两个红点，所以我们在选择覆盖点的时候都选绿点。

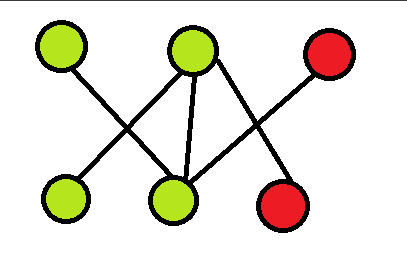
然后又因为如果一个点连接了一个红点，那么与这个点相连的其他的绿点都一定不会连接红点，自己可以画一画，明显可以发现如果连接红点的话，那么刚才所求的就不是最大匹配了。那么对于这些点，我们肯定选择那个连接了红点的点作为覆盖点，因为并不会有其他的点与那个红点相连了。所以可以基本上的出最小覆盖数=最大匹配。

那么我们就把这类问题转化成了网络流了。

4. 最大独立集=总点数-最小覆盖集

这个定理非常好用，不少题目都直接间接的用到了这个东西。先上图：

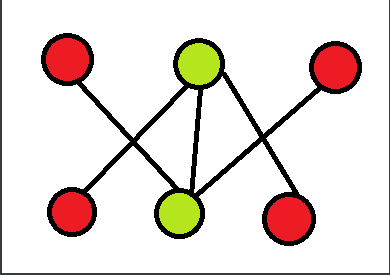
是不是很熟悉，没错就是刚才那个图，笔者实在懒得画另一个了。我们用那两个绿点完成了对这个图的最小覆盖。

然后我们来反证这个结论，即证最小覆盖集+最大独立集$\neq$总点数。

首先我们可以看出除了我们选择的两个用来最小覆盖的点之外，剩下的点之间彼此之间都没有连边，我们可以尝试把任意两个红点之间连一条边，那么明显，我们不满足最小覆盖的要求了，或者我们尝试通过转换使最小覆盖更小。。当然不可行，因为我们已经求得就是最小覆盖了，并且易证的是剩下的所有点一定构成一个独立集。并且这个独立集的大小不能够更大了，然后我们就证出了题目所给的定理。

5.删边

题目不适合起太长，这一部分主要是说：在一个二分图中，如果删去一条边能够使这个图的最大匹配减小1的话，那么这条边一定在残量网络中满流，并且它所连接的两个点一定不在同一个强连通分量当中。

首先满流的条件一定要有，不满流那这条边就不在最大匹配里了。然后就是不在同一个强连通分量里这个条件，我们可以发现，在同一个强连通分量里的话，那他们就可以自己在这个强连通分量的内部进行增广，也就是说我们可以通过操作从而找到另一组最大匹配并且不需要使用当前这条边，所以这条边删掉也就无可厚非了。

6.最小路径覆盖

说一下大意，就是现在有一个有向无环图G，要求用尽量少的不相交的简单路径覆盖所有的节点 。

那么这个也有一个结论，就是最小路径覆盖=原图节点数-最大匹配

诶，等等，哪里来的最大匹配。。

我们对当前的图拆点，把每个节点都拆成x,y两个节点。如果$x_1有一条指向x_2的边，那么就把x_1和y_2之间连一条边$，这样我们就能得到一个二分图了，那么为什么这么做可行呢？

一开始每个点都是独立的为一条路径，总共有n条不相交路径。我们每次在二分图里找一条匹配边就相当于把两条路径合成了一条路径，也就相当于路径数减少了1。所以找到了几条匹配边，路径数就减少了多少。所以有最小路径覆盖=原图的结点数-新图的最大匹配数。

以上就是我们常用的网络流构图的基本思想了，接下来笔者会从做过的题目里挑选出来一些觉得建模比较有代表性的题目分享给大家

九、经典的建模

其实你也可以看出来笔者这个地方写的很青涩，那是早之前写的了，可能对于刚刚入门网络流的人比较有用，但是对于大佬们肯定用处不大了，下面的题目肯定也都有自己独特的见解和理解方式，所以请dalao从6开始看。。。

1.方格取数加强版

注意，这道题和刚才那个不是一道题目。

记不记得我们NOIP曾经考过一道叫做方格取数题目。这道题就是那个题的加强版。本来是要走2次，现在变成了要走n次。。原来的DP方案好像一下子就垮掉了。现在我们来这么考虑，我们把这个题当成一个图论题而不是DP题，那么我们走过的格子就要拿走相应格子的点权，刚才说过什么，如果是点权问题的话，是不是要拆点。那么我们又怎么处理每个格子可以走无数次呢？好办，我们对于每个格子的入点和出点分别连两条边，一条是费用为点权流量为1的边，表示可以取走这个格子里的点权；一条是费用为0流量为inf的边，表示这个格子可以无数次经过。然后相应的建立超级源和超级汇，分别向左上角和右下角连接流量为k的边来限制要走k次这个条件。这样我们是不是就做出了这个题。

2.[CQOI2015]网络吞吐量

这道题就开始慢慢的使建图复杂起来了，我们根据题意可以发现这道题的网络流是严格的按照最短路跑的。等等？按照最短路跑？这和树上跑网络流有个P区别，不直接写出来那个最小的流量O（1）出解更好么？然后笔者就画了画样例模拟了一下，发现这个样例，并不只有一条最短路！！！所以我们先求出来一遍最短路之后，通过遍历一个点的所有出边的方式判定到下一个点的是不是最短路。如果$dis[v]=dis[u]+edge[i].dis$那么我们就找到了到下一个点的一条最短路。然后连边求最短路即可。

3.数字梯形问题

这个题有三问，虽然很相似就是了。让我们一问一问解决这个题目。P.s.把这个题放在这里的意义就是让大家思考一下网络流里连接inf边的道理。

首先先从起点到最上层的每个数字连流量为1的边，表示从这些数字开始走，然后从最下层的每个数字连到汇点，流量为1。

①从梯形的顶至底的 m 条路径互不相交；

这一问就是每个点和每条边都只能用一次的意思，所以练出来流量为1的边跑费用流就可以了。

②从梯形的顶至底的 m 条路径仅在数字结点处相交；

那么我们现在就可以使用重复的点了对不对。。。所以入点和出点的连边我们就可以连inf了，表示这个点可以用无数次。然后我们再跑一遍费用流。

③从梯形的顶至底的 m 条路径允许在数字结点相交或边相交。

话说。。边怎么相交，这个题貌似相交不了。。实际上就是可以经过重复的边，然后我们每个点的出点连向下个点的入点的流量也设置为inf然后我们再跑费用流。

好了，看上去这道题A了，那么交上去试试？然后你就会有这种效果：

为什么，就是因为这一句话 “然后从最下层的每个数字连到汇点，流量为1。”，如果我们这么连边了，那么最后一层的点，就只能使用一次，然后你不就挂掉了。。。所以从第二次开始，我们就要把这条边连inf变成1，然后就可以了。

4. 餐巾计划问题

网络流24题里还是有很好的题目的，比如说这一道，建图方式妥妥的一股清流。首先我们发现这个题的状态很多，首先是两个洗毛巾的操作，这个比较好办，拆点了之后直接去洗就可以了，然后就是这个题目的精髓所在，对于这种直接购买进来的操作，我们往常的思路是向入点连边，然后限制流量，然而这个题我们仅仅只在入点限制流量，而把买餐巾这个操作连到当天的出点上，这样就可以使在洗掉的餐巾不足以支持满流的情况下是这一天满流。然后因为我们有攒着餐巾不使用这种操作，所以我们要把上一天的入点和下一天的入点之间连一条inf的边表示这种情况。

5.[CTSC1999]家园

这个题具体来说就是一个拆门的操作(雾)，先让笔者来说明一下拆门这个操作是什么含义吧。。

笔者有次做了一道叫做紧急疏散的网络流题目，一开始笔者是用时间点建分层图，结果发现不可以这么做，整个题目会爆炸掉，但是这个题又没有更好的方法去支持时间的限制，然后笔者发现可以有拆门这种操作，因为门，也就是指定的汇点的个数总是有限的，哪怕你把这东西拆成500个点，也不会造成有太多边的情况。然后从每天向下一天连边，就可以在一些题目上避免使用分层图造成复杂度过高。

那么这个题我们也可以这么干。首先我们把每天的地球和月球都和超级源点和汇点连inf的边，然后把太空船上一天的位置和这一天的位置连一条容量为太空船装载人数的边，然后再从每一天的向下一天连一条inf边表示可以用人留在这里，我们就可以通过每一天的最大流跑出结果。然后是一个操作，大部分这种题目我们要二分答案，然而二分的代价就是你要有非常繁杂的预处理过程才能保证你建出来的图没有问题，然而这个题的数据范围小到让你可以直接枚举，并且每次不把图清零，而是在已有的残量图上继续跑，从而达到不错的时间效率与较低的代码难度。

---

从这里开始这一个专题要变得不和谐起来了，并且可能有我自己YY的神奇的模型。

6.黑白染色

怎么说呢，黑白染色这东西，很迷。

6.1适用性

黑白染色一定是在棋盘图上，嗯，这点绝对没有问题。然后就是要把棋盘的格子当做点，并且经过了染色之后，你会惊奇的发现黑点只会限制白点，不会限制黑点，白点也只会限制黑点。也就是说同色的点之间并没有直接关系。

6.2为什么使用它

当你拿到一个棋盘的题手足无措，就要被水淹没时，黑白染色很有可能救你一命。黑白染色，一共只有两种颜色，所以这样建图之后一般都会和二分图非常像，然后就是随便匹配的事了。另一种情况是你把这题转化成了一个最小割的模型，发现题目中删去某个点或者添加某个点的操作就是在删边。从而随便网络流跑出来这个题。

6.3模型建立

基本上可以确定的是你选择一个你喜欢的颜色，把它连向你不喜欢的那个颜色，然后你不喜欢的那个颜色去连汇点，你喜欢的连源点。但是问题也就来了，这个东西适用于几乎所有要用到黑白染色的题目，那么也就是说，它没屁用。实际上，真正恶心的一般都在黑白点互相连接的限制上，所以具体问题只能具体分析。

6.4Difficult

然而有的时候发现黑白染色并不能完全解决问题，或者说这个题并不能符合黑白染色的定义。。那么我们就红黄蓝染色，再不行就红黄绿蓝染色。然后重新构造模型。不得不说，这东西有的时候还是能派上大用的。

6.5时间复杂度

黑白染色的题目，我们一定要相信信仰，因为建出来的图基本上都是那种二分图，还是边比较稀疏的那种，所以我们可以几乎在$O(n^{1.5})$的时间复杂度就解决问题，所以不要问为什么有的题1e5的数据都跑网络流了。

7.切糕模型

事先证明，这个鬼畜的名字不是我叫出来的，是网上某个博主这么叫的，然后我一想确实是很有道理。这种模型本来应该叫距离限制模型。也就是说，每个元素选择时，有多种选择，并且相邻两个元素之间的选择会相互限制。例题就是HNOI某一年的一道叫切糕的题目。

其实这个模型挺经典的，但是很多情况下题目不仅仅只是有这样一个限制，然后就被其它的模型覆盖了。

8.最大密度子图

这个事实上都可以单独拿来当成一个题做了。先说一下要求：

给定一个无向图，要求从无向图里抽出一个子图，使得子图中的边数$\mid E\mid$与点数$\mid V\mid$的比值最大，即求最大的$\frac{\mid E\mid}{\mid V\mid}$.

给出一种解法，由前面说过的最大权闭合子图得到的。假设答案为k ，则要求解的问题是：选出一个合适的点集 V 和边集 E，令(|E|−k∗|V|)取得最大值。所谓“合适”是指满足如下限制：若选择某条边，则必选择其两端点。

建图:以原图的边作为左侧顶点，权值为1；原图的点作为右侧顶点，权值为 −k (相当于 支出 $k$)。 若原图中存在边 (u,v)，则新图中添加两条边 ([uv]−>u), ([uv]−>v)，转换为最大权闭合子图。 其中k可以二分得到。

---

锅，突然发现这个东西没证。。。。

然后发现第一步并不能证出来。。。

现在我又证出来了。。。

无向图的子图的密度：$D=\frac{|E|}{|V|}$

看成是分数规划问题，二分答案 λ ，需要求

$g(\lambda)=max(|E|-\lambda|V|)$

g(λ)=0时我们取到最优解。

喏，现在权当我这一步证出来了。

给出证明吧。

给出函数$\lambda=f(x)=\frac{a(x)}{b(x)}(x\in S)$

那么我们猜测一个最优值λ，重新构造一个函数：

$g(\lambda)=max\lbrace a(x)-\lambda b(x)\rbrace$

若我们设一个$\lambda^*=f(x^*)$为最优解，那么则有：

$g(\lambda)<0⇔\lambda>\lambda^*$

$g(\lambda)=0⇔ \lambda=\lambda^*$

$g(\lambda)>0⇔ \lambda<\lambda^*$

似乎貌似就是大于小于的情况要么不合法，要么不够优。当g(λ)=0时正好取到最优解。

然后我们开始思考如何搞出来，可以发现我们选择一条边就要选择与它相连的两个端点。那么，随便YY一下，搞一个如上面的建图，就可以发现上面那个建图满足我们的条件。

可是有个问题，当λ取到一定值的时候，它变大并不会影响最大权闭合图的值，统统都是0.。所以我们二分求得是在g(λ)=0时最小的λ。

9.疏散模型

这个模型就是我自己YY出来的了。前面应该提到过了，我做过一道叫紧急疏散的鬼畜题。这道题让我生生调了半天代码，从此对这题印象深刻。

那么这是一个什么样的模型呢？它利用两个特点，一个是分层图的一些概念，一个是前后缀的思想。明显的是，分层图我们可能在一些题目中看出，然后坑爹的是，这个题分层的话整个题目复杂度极高，时间空间都不支持。这个时候可以尝试只拆开汇点，也就是我之前所说的拆门。然后对于那个时间点能到汇点的点，与这个时刻的门连一条边。然后利用前缀思想，把每一天的汇点一串inf连下去，最后就可以求出。而且时空复杂度都很小啊。

10.优化建图

有这么些题，你一看就知道应该怎么建图，然后仔细看看数据范围，用常规方法不是炸你空间就是让你T掉。。。。这个时候我们可以尝试一下优化，比如说使用数据结构。虽然这东西放出来之后一般人不会愿意打。那么是什么原理呢？如果我们某个区间里的每个点都要互相连边，那么就可以建线段树，然后把对应的区间连边，然后线段树的节点之间互相连边，就可以优化边数。

然而值得注意的是，我并没有写数据结构/优化建图，因为更不正常的题目，我们或许会用到计算几何。十分鬼畜，鬼畜至极。。然而这种题目。。鬼才会去写啊。。。有兴趣的去看看[Jsoi2018]绝地反击 。话说这个优化的原理是什么呢？举个栗子：假设一个题目有很多点，但是你经过各种手玩和证明之后，发现所有不在凸包上的点不会互相连边，这个时候求一发凸包，就可以大大的减少边数了。

11.最长反链和最小链覆盖

在有向无环图中，链是一个点的集合，这个集合中任意两个元素v、u，要么v能走到u，要么u能走到v。

反链是一个点的集合，这个集合中任意两点谁也不能走到谁。

最长反链是反链中最长的那个。

那怎么求呢？

11.1 传递闭包

在开始介绍这个之前，我先简单叙述一下传递闭包是个什么东西。可以发现的是百度百科里的东西都奇怪的一批根本让人看不懂。那么我就尽量通俗的说一下。

传递闭包就是求一个图里面所有满足传递性的点。那么传递性又是什么呢？简单来说就是：假设图中对于图中的节点$i$,若果有一个j点可以到$i$，$i$点又可以到$k$，那么$j$就能到$k$。这样的节点就可以说是有传递性。看上去非常的，简单。其实就是这样。求完传递闭包之后，我们能够知道的是图中的任意两点是否相连。

那么，我们可以用Floyd算法搞出来，没错，就是Floyd。只不过我们现在是求两点是否相连，而不是求其最短路径。

11.2最小链覆盖

这个东西就是求出最长反链的关键。因为：最小链覆盖=最长反链长度。

那么，最小链覆盖又怎么求出呢？

回想一下我们之前是不是有一个地方介绍过了最小路径覆盖。那个地方所求的是不能相交的最小路径覆盖，那么这里我们要求的就是路径可以相交的最小路径覆盖。

问题又来了，这个又怎么求解呢？

我们把原来的图做一遍传递闭包，然后如果任意两点$x,y$,满足$x$可以到达$y$，那么我们就在拆点后的二分图里面连一条$(x_1,y_2)$的边。

这样球可以绕过一些在原图中被其他路径占用的点，构造新的路径从而求出最小路径覆盖。

那么这样我们就把可以相交的最小路径覆盖转化为了路径不能相交的最小路径覆盖了。 从而我们求出了这个图的最小链覆盖。

11.3 十分感性的证明

那么我们证明一下刚才一个结论的正确性。

我们通过观察定义可以得出，最长反链的点一定在不同的链里。所以最长反链长度$\le$最小链覆盖数。

那么我们接着可以通过感性理解和数学归纳证出最长反链长度$\ge$最小链覆盖数.

如此我们就能够得证了。

11.4最长链长度 = 最小反链覆盖数

不想证了。这个结论就是上面的反向结论，其实直接背过就可以了。。。。。

12.混合图的欧拉回路

12.1欧拉回路

(1)给定一个图G，假设我们能一笔画，如果图G中的一个路径包括每个边恰好一次，则该路径称为欧拉路径(Euler path)。如果一个回路是欧拉路径，则称为欧拉回路(Euler circuit)。
具有欧拉回路的图称为欧拉图（简称E图）。具有欧拉路径但不具有欧拉回路的图称为半欧拉图。

(2)对于一个无向图，如果每个点的度数均为偶数，那么这个图是一个欧拉图。

(3)对于一个有向图，如果每个点的出度都等于入度，那么这个图是一个欧拉图。

(4)对于无向图，如果每个点度数均为偶数，或者有且仅有两个顶点度数为奇数，那么这个图中存在欧拉路径。

(5)对于有向图，如果每个点的出度等于入度，或者有且仅有两个点不符，且这两个点一个入度比出度小1，一个出度比入度小1，则这个图存在欧拉路径。

12.2求解一般欧拉图

直接暴力枚举所有点的出度入度即可，用上面的关系进行判断，可以求出。

12.3求解混合欧拉图

明显，不能通过刚刚的方法来套用到这个题上去。

对于这种图，我们首先可以自定向无向边的方向。可以rand，也可以规定一个方向从而全部指向一个方向。不过这样无法直接得到答案，说不定脸好，但是我们可以通过这样一个操作搞出来一个完全有向的图，可以套用上面的性质来初步判断这个题是否有欧拉回路。不过这样做明显没有依据，只是一个预处理的过程，再通过调整判断是否有解。

那么如何自调整呢？引用一段话：

所谓的自调整方法就是将其中的一些边的方向调整回来，使所有的点的出度等于入度。但是有一条边的方向改变后，可能会改变一个点的出度的同时改变另一个点的入度，相当于一条边制约着两个点。同时有些点的出度大于入度，迫切希望它的某些点出边转向；而有些点的入度大于出度，迫切希望它的某些入边转向。这两条边虽然需求不同，但是他们之间往往一条边转向就能同时满足二者。

然后我们发现，网络流貌似可以满足这个自调整的性质。

12.4算法步骤

1.$首先对于每个入度>出度的点，我们将其与源点S连接一条权值为\frac{入度-出度}{2}的边；$

$对于每个入度<出度的点，我们将其与汇点T连接一条权值为\frac{出度-入度}{2}的边。$

为什么除以2，因为我们改变一条边的方向时，会造成出度和入度的改变，所以。。。

2.然后将原图中所有你定了向的无向边连接的两个点连一条边权为1，方向为你定向方向的无向边。

3.跑网络流去，如果满流自然就有解。

4.把在网络流中那些因为原图无向边而建的流量为1的边中经过流量的边反向，就形成了一个能跑出欧拉回路的有向图，如果要求方案，用有向图求欧拉回路的方法求解即可 。

13.最大权闭合子图

发现前面写最小割的时候把这个东西跳过去了，。。。现在补上。

13.1定义

一个子图（点集）， 如果它的所有的出边所指向的点都在这个子图当中，那么它就是闭合子图。 点权和最大的闭合子图就是最大闭合子图。

13.2构图

设置超级源汇S，T。

然后使S和所有的正权的点连接权值为点权的边，所有点权为负的点和T连接权值为点权绝对值的边。然后如果选择了某个v点才可以选u点，那么把u向v连接一条权值为$\infty$的边。

然后随便跑跑网络流。

最大点权和=正点权和-最小割。

13.3并不感性的证明

首先说简单割，就是我们求最小割的时候每条割边都与S或T相连。在闭合图中，由于我们不与S或T连接的边的权值都是inf，所以我们不会割到他们。容易得证闭合图中的最小割是简单割。

接着证明简单割和闭合图的关系。

因为简单割不会含有那些正无穷的边，所以不含有连向另一个集合(除T)的点，所以其出边的终点都在简单割中，满足闭合图定义。

我们假设跑完最小割之后的图中一共有两部分点$X,Y$，$X$表示与S相连的点，$Y$表示与T相连的点，那么我们可以设$X_0,Y_0$为负权点，$X_1,Y_1$为正权点。然后由于我们求了一遍最小割，根据上面简单割的证明我们发现不会割去中间inf的边，所以我们可以求出：

$最小割=|X_0|+|Y_1|$

刚才已经证明过X，Y均是闭合图。

然后我们可以发现X的权值和可以表示为$Sum_X=X_1-|X_0|$

我们把上面那个式子代入到这个式子里。

$Sum_X+最小割=X_1-|X_0|+|X_0|+Y_1$

然后我们得出：

$Sum_X+最小割=X_1+Y_1=原图所有正权点权值之和$

然后我们得证。

14.文理分科模型

本来不想整理这个，因为确实不是特别的突出，用的地方也不是很多。然后，笔者在写这个东西的这一天连着看见两道这样的题。所以还是整理一下。

这里表示如果点的贡献不仅仅是点权，而且还有附加的条件的话，比如同时选A，同时选B，选择不相同。。。。。

那么我们就利用最小割的性质构造一下即可。用“割掉”代表选择。

然后分情况讨论所有选择情况，使对应情况下被割掉的边流量之和等于权值 即可。

---

到这里这个课件的系统知识部分就已经结束了，然而还是有不小的漏洞，比如线性规划，比如有上下界的网络流，比如流量平衡等等。不过笔者自信自己的绝对是目前网上能找到的最全的一个了。

十、几道脑洞大开的题目

这些题大多比较新，都是这两年的新题，并且建模的思路极其鬼畜新颖，所以还是很值得一看的。不，是很值得一看，而且我在这里写的题解确实，十分详细。。。。

---

1.[SDOI2017]新生舞会

题面描述

学校组织了一次新生舞会，Cathy作为经验丰富的老学姐，负责为同学们安排舞伴。

有nn 个男生和nn 个女生参加舞会买一个男生和一个女生一起跳舞，互为舞伴。

Cathy收集了这些同学之间的关系，比如两个人之前认识没计算得出 $a_{i,j}$

Cathy还需要考虑两个人一起跳舞是否方便，比如身高体重差别会不会太大，计算得出 $b_{i,j}$ ，表示第i个男生和第j个女生一起跳舞时的不协调程度。

当然，还需要考虑很多其他问题。

Cathy想先用一个程序通过$a_{i,j}$和$b_{i,j}$ 求出一种方案，再手动对方案进行微调。

Cathy找到你，希望你帮她写那个程序。

一个方案中有n对舞伴，假设没对舞伴的喜悦程度分别是$a'_1,a'_2,...,a'_n$，假设每对舞伴的不协调程度分别是$b'_1,b'_2,...,b'_n$ 。令

C=$\frac{a'_1+a'_2+...+a'_n}{b'_1+b'_2+...+b'_n}′$

Cathy希望C值最大。

数据范围

对于100%的数据，$1\le n\le 100,1\le a_{i,j},b_{i,j}<=10^4$

Solution

这个题乍一看上去很是让人束手无策，DP明显被强大的后效性D掉了，据说有线性规划的做法，但是笔者并没有想出来，搜索的话n=100让人很是头疼。那么现在没有什么办法，我们就只能再回到题目里面去看看有没有什么没有发现的信息。

然后我们发现了这个东西：C=$\frac{a'_1+a'_2+...+a'_n}{b'_1+b'_2+...+b'_n}′$

我们发现这个分式一定有意义，那么分母不可能为0，又因为给的都是正整数，所以分母大于0。

那么首先我们先去分母，这个式子就变成了：$(b'_1+b'_2+\cdots+d'_n)\times C=(a'_1+a'_2+\cdots+a'_n)$

然后我们移项，它就成了$(a'_1+a'_2+\cdots+a'_n)-(b'_1+b'_2+\cdots+d'_n)\times C=0$

然后我们去括号，就变成了：$a'_1+a'_2+\cdots+a'_n-b'_1\times C-b'_2\times C-\cdots-b'_n\times C=0$

为了方便计算，我们可以合并一下同类项：$(a'_1-b'_1\times C)+(a'_2-b'_2\times C)+\cdots+(a'_n-b'_n\times C)=0$

我们题目中要求的式子就和现在的式子一样了。

此时我们就可以二分C值，然后判断tot是否大于或小于0来缩小边界。

然后我们发现每个{a,b}数对的下标都是一一对应的，所以我们直接从第i个男生想第j个女生连接一条$a_i-b_i\times C$的边就可以了。

说了从这里开始就会有代码。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#define inf 1000000000000001ll
#define maxxx 500000001
#define re register
#define ll long long
#define min(a,b) a<b?a:b 
using namespace std;
const long double eps=0.00000007;
struct po{
    int to,nxt,w;
    ll dis;
};
po edge[800001];
int n,m,s,t,b[205],p;
int head[205],num=-1;
ll tot,dis[205],pa[501][501],pb[501][501];
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch>'9'||ch<'0')&&ch!='-')ch=getchar();
    while(ch=='-')c*=-1,ch=getchar();
    while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
inline void add_edge(int from,int to,int w,ll dis)
{
    edge[++num].nxt=head[from];
    edge[num].to=to;
    edge[num].w=w;
    edge[num].dis=dis;
    head[from]=num;
}
inline void add(int from,int to,int w,ll dis)
{
    add_edge(from,to,w,dis);
    add_edge(to,from,0,-dis);
}
inline bool spfa()
{
    for(re int i=s;i<=t;i++) dis[i]=inf+1;
    memset(b,0,sizeof(b));
    queue<int> q;
    q.push(t);
    dis[t]=0;
    b[t]=1;
    while(!q.empty()){
        int u=q.front();
        q.pop();
        b[u]=0;
        for(re int i=head[u];i!=-1;i=edge[i].nxt){
            int v=edge[i].to;
            if(edge[i^1].w>0&&dis[v]>dis[u]-edge[i].dis){
                dis[v]=dis[u]-edge[i].dis;
                if(!b[v]){
                    b[v]=1;
                    q.push(v);
                }
            }
        }
    }
    return dis[s]<inf;
}
inline int dfs(int u,int low)
{
    b[u]=1;
    if(u==t) return low;
    int diss=0;
    for(re int i=head[u];i!=-1;i=edge[i].nxt){
        int v=edge[i].to;
        if(edge[i].w&&!b[v]&&dis[v]==dis[u]-edge[i].dis){
            int check=dfs(v,min(edge[i].w,low));
            if(check){
                tot+=check*edge[i].dis;
                low-=check;
                diss+=check;
                edge[i].w-=check;
                edge[i^1].w+=check;
                if(low==0) break;
            }
        }
    }
    return diss;
}
inline void max_flow()
{
    int ans=0;
    while(spfa()){
        b[t]=1;
        while(b[t]){
            memset(b,0,sizeof(b));
            ans+=dfs(s,maxxx);
        }
    }
    return;
}
inline void build(ll x)
{
    memset(head,-1,sizeof(head));
    num=-1;tot=0;
    for(re int i=1;i<=n;i++)
    add(s,i,1,0),add(n+i,t,1,0);
    for(re int i=1;i<=n;i++)
     for(re int j=1;j<=n;j++)
     add(i,j+n,1,-(pa[i][j]-pb[i][j]*x));
}
inline bool check(ll x)
{
    build(x);
    max_flow();
    if(-tot<=0) return 1;
    else return 0;
}
int main()
{
    n=read();
    for(re int i=1;i<=n;i++) 
     for(re int j=1;j<=n;j++)
     pa[i][j]=read(),pa[i][j]*=5000000;
    for(re int i=1;i<=n;i++)
     for(re int j=1;j<=n;j++)
     pb[i][j]=read();
     s=0,t=n+n+1;
    ll l=1,r=50000000000ll;
    while(r>=l){
        ll mid=(l+r)/2;
        if(check(mid))
        r=mid-1; else
        l=mid+1;
    }
    printf("%.6lf",l*1.0/5000000);
}

这个题要用数组写费用流，卡了结构体。。。。

2.[HAOI2017]新型城市化

题目描述

Anihc国有n座城市.城市之间存在若一些贸易合作关系.如果城市x与城市y之间存在贸易协定.那么城市文和城市y则是一对贸易伙伴(注意:(x,y)和(y,x))是同一对城市)。

为了实现新型城市化.实现统筹城乡一体化以及发挥城市群辐射与带动作用.国 决定规划新型城市关系。一些城市能够被称为城市群的条件是:这些城市两两都是贸易伙伴。 由于Anihc国之前也一直很重视城市关系建设.所以可以保证在目前已存在的贸易合作关系的情况下Anihc的n座城市可以恰好被划分为不超过两个城市群。

为了建设新型城市关系Anihc国想要选出两个之前并不是贸易伙伴的城市.使这两个城市成为贸易伙伴.并且要求在这两个城市成为贸易伙伴之后.最大城市群的大小至少比他们成为贸易伙伴之前的最大城市群的大小增加1。

Anihc国需要在下一次会议上讨论扩大建设新型城市关系的问题.所以要请你求出在哪些城市之间建立贸易伙伴关系可以使得这个条件成立.即建立此关系前后的最大城市群的 大小至少相差1。

输入输出格式

输入格式:

第一行2个整数n,m.表示城市的个数,目前还没有建立贸易伙伴关系的城市的对数。

接下来m行,每行2个整数x,y表示城市x,y之间目前还没有建立贸易伙伴关系。

输出格式:

第一行yi个整数ans，表示符合条件的城市的对数.注意(x,y)与(y,x)算同一对城市。

接下来Ans行,每行两个整数,表示一对可以选择来建立贸易伙伴关系的城市。对于 一对城市x,y请先输出编号更小的那一个。最后城市对与城市对之间顺序请按照字典序从小到大输出。

输入输出样例

输入样例#1：

5 3
1 5
2 4
2 5

输出样例#1：

2
1 5
2 4

说明

数据规模与约定

数据点1： n≤16

数据点2： n≤16

数据点3~5： n≤100

数据点6： n≤500

数据点7~10： n≤10000

对于所有的数据保证：n <= 10000,0 <= m <= min (150000,n(n-1)/2).保证输入的城市关系中不会出现(x,x)这样的关系.同一对城市也不会出现两次(无重边.无自环)。

Solution

既然把题放在这里了，那么自然就不会像题解里写的solution一样了。

其实这个题的主体思路在前面的几个分块中没有来的及体现出来，涉及到二分图的问题。这也是笔者一个失误，二分图类的问题一定近期补到前面去。

那么我们继续来看这道题。题目给出的是一些城市之间的关系。然后看那个城市群的定义，这些城市两两之间能够互相到达。加上给出的城市之间的关系是之间没有路径能够互相到达，那么就比较明显了，如果我们根据题目中要求把城市连起来，那么我们一定可以得到一个二分图。（为什么忽略了只能是一个城市群的情况？？因为就一个城市群你也没有可以建立的关系了，这么出题没有意义。）

然后我们仔细考虑这个题让我们干什么，在两个本来没有关系的城市之间建立关系，就是从我们刚刚建立的二分图里面删去一条边，最大城市群的大小增加1，就是让我们这个二分图里的最大独立集增加1。又因为定理：最大独立集=总点数-最小覆盖集=最大匹配。所以我们要求的就是删去一条边可以使二分图的最大匹配减小1的总边数。然后我们可以用网络流来实现。

那么我们现在就有了一个初步的做法了，大体思路就是枚举所有的边，然后不停的网络流，之后慢慢的计算有那些边可以删掉。不过这样过5个点也就差不多快超时了，网络上有大佬说退流或许能够达到更好的时间效率，不过我看上去并没有从根本上优化算法，所以过掉第6个点还是悬。那么我们有没有更优化的方法呢？

有的，根据定理：若一条边一定在最大匹配中，则在最终的残量网络中，这条边一定满流，且这条边的两个顶点一定不在同一个强连通分量中。 可得，我们只需要通过残量网络跑一遍Tarjan就可以了。那么这个定理又是怎么来的呢。。（话说为什么有这么多的定理。）

笔者浅显的证明一下：首先要满流，然后不在同一个强连通分量里是指，如果在同一个强连通分量里，那么我们在这个强连通分量内部增广一下，整个分量里的残量都会变化，但是网络的最大匹配并不会变化，也就是说我们又能得到一个新的最大匹配，也就是说这条边的存在是无可厚非的。

那么可以放上代码了。

Code

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include <iostream>
#include <cstdlib>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <queue>
#include <set>
#include <map>
#define MAXN 200000
#define re register
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(arr) memset(arr, 0, sizeof(arr))
const int inf = 0x3f3f3f3f;
struct po
{
    int nxt,to,w,from;    
}edge[250001];
struct ANS
{
    int x,y;
}ans[MAXN];
int n,m,cur[MAXN],head[20002],num=-1,dep[20002],s,t,c[MAXN],vis[20002];
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch>'9'||ch<'0')&&ch!='-')ch=getchar();
    while(ch=='-') c*=-1,ch=getchar();
    while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
inline void add_edge(int from,int to,int w)
{
    edge[++num].nxt=head[from];
    edge[num].from=from;
    edge[num].to=to;
    edge[num].w=w;
    head[from]=num;
}
inline void add(int from,int to,int w)
{
    add_edge(from,to,w);
    add_edge(to,from,0);
}
inline bool bfs()
{
    memset(dep,0,sizeof(dep));
    queue<int> q;
    while(!q.empty())
    q.pop();
    q.push(s);
    dep[s]=1;
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(re int i=head[u];i!=-1;i=edge[i].nxt)
        {
            int v=edge[i].to;
            if(dep[v]==0&&edge[i].w>0)
            {
                dep[v]=dep[u]+1;
                if(v==t)
                return 1;
                q.push(v);
            }
        }
    }
    return 0;
}
inline int dfs(int u,int dis)
{
    if(u==t)
    return dis;
    int diss=0;
    for(re int& i=cur[u];i!=-1;i=edge[i].nxt)
    {
        int v=edge[i].to;
        if(edge[i].w!=0&&dep[v]==dep[u]+1)
        {
            int check=dfs(v,min(dis,edge[i].w));
            if(check!=0)
            {
                dis-=check;
                diss+=check;
                edge[i].w-=check;
                edge[i^1].w+=check;
                if(dis==0) break;
            }
        }
    }
    return diss;
}
inline void dinic()
{
    while(bfs())
    {
        for(re int i=s;i<=t;i++)
        cur[i]=head[i];
        while(int d=dfs(s,inf));
    }
}
void put_color(int u,int col)
{
    c[u]=col;
    vis[u]=1;
    for(re int i=head[u];i!=-1;i=edge[i].nxt){
        int v=edge[i].to;
        if(!vis[v]) put_color(v,col^1);
    }
}
int dfn[MAXN],low[MAXN],stack[MAXN],color_num,color[MAXN],cnt,top;
inline void Tarjan(int u)
{
    dfn[u]=low[u]=++cnt;
    vis[u]=1;
    stack[++top]=u;
    for(re int i=head[u];i!=-1;i=edge[i].nxt){
        if(!edge[i].w){
            int v=edge[i].to;
            if(!dfn[v]){
                Tarjan(v);
                low[u]=min(low[u],low[v]);
            } else if(vis[v]) low[u]=min(low[u],dfn[v]);
        }
    }
    if(dfn[u]==low[u]){
        color[u]=++color_num;
        vis[u]=0;
        while(stack[top]!=u){
            color[stack[top]]=color_num;
            vis[stack[top--]]=0;
        }
        top--;
    }
}
int x[MAXN],y[MAXN],tot;
inline bool cmp(ANS a,ANS b){
    return a.x==b.x?a.y<b.y:a.x<b.x;
}
int main() 
{
    memset(head,-1,sizeof(head));
    n=read();m=read();
    for(re int i=1;i<=m;i++){
        x[i]=read();y[i]=read();
        add_edge(x[i],y[i],0);
        add_edge(y[i],x[i],1);
    }
    for(re int i=1;i<=n;i++)
        if(!vis[i]) put_color(i,2);
    memset(head,-1,sizeof(head));
    s=0,t=n+1;num=-1;
    for(re int i=1;i<=n;i++){
        if(c[i]==2)
            add(s,i,1);
        else add(i,t,1);
    }
    for(re int i=1;i<=m;i++){
        if(c[x[i]]==2)
            add(x[i],y[i],1);
        else add(y[i],x[i],1);
    }
    dinic();
    memset(vis,0,sizeof(0));
    for(re int i=1;i<=n;i++)
        if(!dfn[i]) Tarjan(i);
    for(re int i=0;i<=num;i+=2){
        int u=edge[i].from,v=edge[i].to;
        if(!edge[i].w&&color[u]!=color[v]&&u!=s&&v!=t&&u!=t&&v!=s){
            if(u>v) swap(u,v);
            ans[++tot].x=u;ans[tot].y=v;
        }
    }
    sort(ans+1,ans+tot+1,cmp);
    cout<<tot<<endl;
    for(re int i=1;i<=tot;i++)
        printf("%d %d\n", ans[i].x,ans[i].y);
    return 0;
}
/*6 5 3 7 2 4 1*/

5.带花树算法

带花树算法用于一般图的最大匹配，而这往往是其他算法所不能做到的。

#include <iostream>
#include <cstdlib>
#include <cmath>
#include <string>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <set>
#include <map>
#define re register
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define MAXN 5001
#define MAXM 1000001
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(arr) memset(arr, 0, sizeof(arr))
const int inf = 0x3f3f3f3f;
int f[MAXN],head[MAXN],next[MAXN],num,match[MAXN],t,vis[MAXN],mark[MAXN],n;
//f是并查集，match是匹配数组，mark表示S/T点。
int x[MAXN],y[MAXN],L;
struct po
{
    int from,nxt,to;
}edge[MAXM];
queue<int> q;
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch>'9'||ch<'0')&&ch!='-')ch=getchar();
    while(ch=='-') c*=-1,ch=getchar();
    while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
int find(int x)
{
    return f[x]==x?f[x]:f[x]=find(f[x]);
}
inline void add_edge(int from,int to)
{
    edge[++num].nxt=head[from];
    edge[num].to=to;
    head[from]=num;
}
inline void add(int from,int to)
{
    add_edge(from,to);
    add_edge(to,from);
}
inline int lca(int x,int y)//朴素找lca，虽然笔者自己是死记硬背的。。貌似只会树剖找lca。。
{
    t++;
    while(1){
        if(x){
            x=find(x);//点要对应到相应的花上。
            if(vis[x]==t) return x;
            vis[x]=t;
            if(match[x]) x=next[match[x]];
            else x=0;
        }
        swap(x,y);
    }
}
inline void flower(int a,int p)
{
    while(a!=p){
        int b=match[a],c=next[b];
        if(find(c)!=p) next[c]=b;
        //next数组是用来标记花中的路径，结合match就实现了双向链表的功能。
        //我们可以知道一个奇环里的所有点只要向外面连边就有可能与外面匹配，所以所有奇环中的点都         
　　　　//要变成S型点扔到队列中。又因为环内部肯定是匹配饱和的，所以这一堆点最多只能匹配出来一             
　　　　//个点，所以每次匹配到一个点就可以跳出循环了。
        if(mark[b]==2) q.push(b),mark[b]=1;
        if(mark[c]==2) q.push(c),mark[c]=1;
        f[find(a)]=find(b);f[find(b)]=find(c);
        a=c;
    }
}
inline void work(int s)
{
    for(re int i=1;i<=n;i++)
        next[i]=mark[i]=vis[i]=0,f[i]=i;//每个阶段都需要重新标记
    while(!q.empty()) q.pop();
    mark[s]=1;q.push(s);
    while(!q.empty()){
        if(match[s]) return;
        int x=q.front();q.pop();//队列中的点均为S型
        for(re int i=head[x];i;i=edge[i].nxt){
            int y=edge[i].to;
            if(match[x]==y) continue;//x与y是配偶，忽略掉
            if(find(x)==find(y)) continue;//x与y在一朵花里，忽略掉
            if(mark[y]==2) continue;//y是T形点，忽略掉。
            if(mark[y]==1) {//y是s型点，需要缩点
                int r=lca(x,y);
                if(find(x)!=r) next[x]=y;//x和r不在同一个花朵， next标记花朵内的路径
                if(find(y)!=r) next[y]=x;//同上
                flower(x,r);flower(y,r);//将r--x--y--r缩成一个点
            }
            else if(!match[y]){//y没有匹配过，可以增广
                next[y]=x;
                for(re int u=y;u;){//增广操作
                    int v=next[u],w=match[v];
                    match[v]=u;match[u]=v;u=w;
                }
                break;
            } else {//y点已经匹配过，将其配偶作为S型点拉进来，y点本身为T型点，继续搜索。
                next[y]=x;
                mark[match[y]]=1;
                q.push(match[y]);
                mark[y]=2;
            }
        }
    }
}
inline void out(){
    for(re int i=1;i<=n;i++)
            if(!match[i]){
                printf("NO\n");
                return;
            }
        printf("YES\n");
}
int main() 
{
    //freopen("date.in","r",stdin);
    while(cin>>n){
        memset(match,0,sizeof(match));
        memset(head,0,sizeof(head));num=0;t=0;
        for(re int i=1;i<=n;i++)
            x[i]=read(),y[i]=read();
        L=read();
        for(re int i=1;i<=n;i++)
            for(re int j=i+1;j<=n;j++){
                if(abs(x[i]-x[j])+abs(y[i]-y[j])<=L){
                    add(i,j);
                }
            }
        for(re int i=1;i<=n;i++)
            if(!match[i]) work(i);
        out();
    }
    return 0;
}

6.最小生成树

利用克鲁斯卡尔算法。

注意边加到$n-1$条就要跳出。

6.1 克鲁斯卡尔重构树

就是在实现最小生成树的时候，每发现一条新的链接点$(x,y)$的边，就新建一个节点$T$，并且将$x$和$y$分别连接到$T$上。

这样最后就能得到一个二叉树。

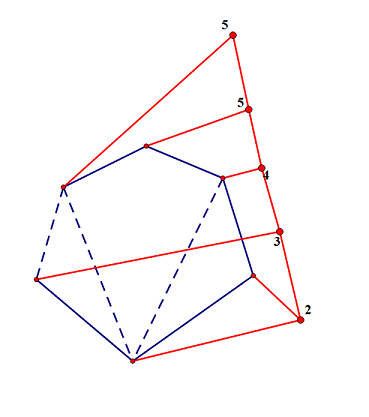
这样弄出来一个树就能具有一些性质。

· 1.生成一个大根堆。
· 2.任意两点间权值最大的边是其最近公共祖先。

这样可以发现，假定一个限制$x$，则利用边权小于$x$的边能够联通的点就是所有重构树的点权小于$x$的点的子树能到达的所有根节点。

相似的，可以建立反向的重构树从而查出两点间最小的边权。

for(int i=1;i<=m;++i)
      {
        if(num==n-1) break;
        int r1=find(c[i].x),r2=find(c[i].y);
        if(r1==r2) continue;
        ++num,fa[++cnt]=cnt,f[0][r1]=f[0][r2]=cnt,v[cnt]=c[i].dis,fa[r1]=fa[r2]=cnt;//cnt表示新建点编号，注意应该从n开始编号
        add(cnt,r1),add(cnt,r2);//从cnt向r1,r2连边
      }//建树

6.2最小生成树计数

未补

三、数论

1.线性筛

经常写经常忘。

inline void get_list()
{
    prime[1]=2;
    pr[1]=1;
    for(re int i=2;i<=n;i++){
        if(!pr[i]) prime[++tot]=i;
        for(re int j=1;j<=tot&&i*prime[j]<=n;j++){
            pr[i*prime[j]]=1;
            if(i%prime[j]==0) break;
        }
    }
}

2.欧拉函数

在数论中，对正整数n，欧拉函数是小于或等于n的正整数中与n互质的数的数目（因此$φ(1)=1$）。

通式：

$$\varphi(x) = x\prod_{i=1}^n(1-\frac{1}{p_i})$$ $p_i$为x的所有质因数

性质：

（1）欧拉函数是积性函数，所以有$\varphi(mn)=\varphi(m)\varphi(n)$

（2）若$x$是质数，则有$\varphi(x)=n-1$

（3）若$x$是不为$2$的质数，则有$\varphi(2x)=\varphi(x)$

（4）若有$i\%p=0$,则有$\varphi(i*p)=p*\varphi(p)$

（5）欧拉定理：即$x^{\varphi(n)}\equiv1(mod\ n)$，则有$x$的逆元为$x^{\varphi(n)-1}$

（6）对于欧拉定理，在$n$为质数时，有费马小定理,即$x$的逆元为$x^{n-2}$

（7）若$x$与$p$互质，则$p-x$ 也与$p$互质，则有对于任意$x$，其小于$p$且与$p$互质的数的和为$\frac{\varphi(x)*x}{2}$

对于求欧拉函数，可以有类似于线性筛的方法求。

for(int i=2;i<=n;i++)
        if(euler[i]==i)
            for(int j=i;j<=n;j+=i)
                euler[j]=euler[j]/i*(i-1);

3.乘法逆元

定义：若在$mod\ p$的意义下，对于一个数$x$，有$x*y\equiv1(mod\ p)$，则称$y$为$x$的乘法逆元，同时$x$也为$y$的乘法逆元。一个数有乘法逆元的充分要素是对于$x$和$p$有$gcd(x,p)=1$，则$x$有$(mod\ p)$意义下的乘法逆元。

用途：除法取模，在除法中模法结合律失效，故只能使用逆元。

求法：

（1）费马小定理，上面已经叙述过。

ll pow(ll a, ll n, ll p)    //快速幂 a^n % p
{
    ll ans = 1;
    while(n)
    {
        if(n & 1) ans = ans * a % p;
        a = a * a % p;
        n >>= 1;
    }
    return ans;
}
ll niyuan(ll a, ll p)   //费马小定理求逆元
{
    return pow(a, p - 2, p);
}

（2）扩展欧几里得法

由于有，当$bx\%p=1$，则$bx+py=1$$(p=0，求x)$,则利用exgcd可以直接求出逆元。

g=exgcd(m,p,x,y);
inline int exgcd(int a,int b,int &x,int &y)//exgcd 
{
    if(b==0){
        x=1;y=0;
        return a;
    }
    int g=exgcd(b,a%b,x,y);//(x即为所求得的逆元)
    int t=x;
    x=y;y=t-a/b*y;
    return g;
}

（3）线性递推

对于一个质数$p$，可以进行线性递推。

    inv[1]=1;
    for(int i=2;i<=n;i++) inv[i]=(ll)(p-p/i)*inv[p%i]%p;//线性递推 

4.扩展欧几里得

欧几里得算法用于计算最大公约数问题。

扩展欧几里得算法是欧几里得算法（又叫辗转相除法）的扩展。除了计算a、b两个整数的最大公约数，此算法还能找到整数$x$、$y$（其中一个很可能是负数）。通常谈到最大公因子时, 我们都会提到一个非常基本的事实: 给予二整数 $a$ 与 $b$, 必存在有整数$x$ 与 $y$ 使得$ax + by = gcd(a,b)$。有两个数$a$,$b$，对它们进行辗转相除法，可得它们的最大公约数——这是众所周知的。然后，收集辗转相除法中产生的式子，倒回去，可以得到$ax+by=gcd(a,b)$的整数解。

5.卢卡斯定理

对于组合数$C_n^mmod\ p$，并且$p$足够小，可以使用卢卡斯定理求。

//核心思想C(n,m)%p=C(n%p,M%p)*C(n/p,m/p)%p 
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define int ll 
const int MAXN=2e5+7;
int n,m,p,fac[MAXN];
inline int ksm(int k,int x)
{
    int cnt=1;
    while(x){
        if(x&1) cnt=cnt*k%p;
        x>>=1;k=k*k%p;cnt%=p;
    }
    return cnt%p;
}
inline int C(int k,int b){return k<b?0:(fac[k]*ksm(fac[b],p-2))%p*ksm(fac[k-b],p-2)%p;}
inline int lucas(int k,int b){return b==0?1:C(k%p,b%p)*lucas(k/p,b/p)%p;}
main()
{
    int T;
    cin>>T;
    while(T--){
        cin>>n>>m>>p;
        fac[0]=1;
        for(int i=1;i<=2e5;i++) fac[i]=(fac[i-1]*i)%p;
        int d=lucas(n+m,m);
        cout<<d%p<<endl;
    }
}

特别的，对于$n,p$很大，而$m$足够小的题目，可以使用exgcd直接求出解。

    #include<bits/stdc++.h>
    using namespace std;
    // A*x0 + B*y0 = B*x + (A-A/B*B) *y
    // A*x0 + B*y0 = A*y + B * (x-A/B*y) 
    int extgcd(int A,int B,int &x,int &y){
        if( B == 0 ){
            x = 1;
            y = 0;
            return A; 
        }
        int gcd = extgcd(B, A%B, x, y);
        int x0 = y;
        int y0 = x - A / B * y;
        x = x0;
        y = y0;
        return gcd;
    }
    // A * x = 1 ( mod P ) = > A * x + P * y = 1
    int getInv(int A,int p){
        int x, y, gcd = extgcd(A,p,x,y);
        if( gcd != 1)return -1; // 扩展欧几里得无法求出逆元 
        p /= gcd;
        return ( x % p + p ) % p; // 取最小正整数解 
    }
    int main(){
        int i, n, r, p, ans = 1, inv;
        cin >> n >> r >> p;
        for( i = 1; i <= r; ++ i, -- n){
            ans = ans * n % p;
            if( ans % r == 0 ) ans /= r; //如果可以除掉 就不要求逆元 
            else if( r >= 2 ){ // 1不需要求逆元 
                inv = getInv(r,p);
                if( inv == -1 ){
                    cout << "扩展欧几里得无法求出逆元,该程序无法求解"<<endl;
                    return  0;
                }
                ans = ans * inv % p;
            }
        }
        cout << ans;
        return 0;
    }

6.中国剩余定理

通俗来讲，中国剩余定理及给出一个一元线性同余方程组，如：

有解的判定条件，并且给出了如何求解。

如果解在$mod\ M(M=m_1m_2...m_n)$下是唯一的，则有$S\equiv(a_1M_1M_1^{-1}+a_2M_2^{-1}+...+a_nM_nM_n^{-1})(mod\ M)$

其中$M_i^{-1}$为$M_i$的乘法逆元。

const LL maxn = 20;
LL a[maxn], m[maxn], n;
LL CRT(LL a[], LL m[], LL n)
{
    LL M = 1;
    for (int i = 0; i < n; i++) M *= m[i];
    LL ret = 0;
    for (int i = 0; i < n; i++)
    {
        LL x, y;
        LL tm = M / m[i];
        ex_gcd(tm, m[i], x, y);
        ret = (ret + tm * x * a[i]) % M;
    }
    return (ret + M) % M;
}

扩展:上述方法并不适用于$m_i$不互质的情况。

const LL maxn = 1000;
LL a[maxn], m[maxn], n;
LL CRT(LL a[], LL m[], LL n) {
    if (n == 1) {
        if (m[0] > a[0]) return a[0];
        else return -1;
    }
    LL x, y, d;
    for (int i = 1; i < n; i++) {
        if (m[i] <= a[i]) return -1;
        d = ex_gcd(m[0], m[i], x, y);
        if ((a[i] - a[0]) % d != 0) return -1;   //不能整除则无解
        LL t = m[i] / d;
        x = ((a[i] - a[0]) / d * x % t + t) % t; //第0个与第i个模线性方程的特解
        a[0] = x * m[0] + a[0];
        m[0] = m[0] * m[i] / d;
        a[0] = (a[0] % m[0] + m[0]) % m[0];
    }
    return a[0];
}

7.高斯消元

作用：求$n$元一次方程组。

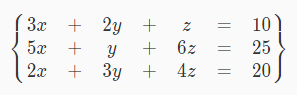
就这样的。

#include <bits/stdc++.h>
using namespace std;
const int MAXN=1e5+7;
#define ll long long
const double eps=1e-8;
double a[105][105],del;
int n;
inline bool gauss()
{
    for(int i=1;i<=n;i++){
        int k=i;
        for(int j=i+1;j<=n;j++) if(fabs(a[j][i]>fabs(a[k][i]))) k=j;
        if(fabs(del=a[k][i])<eps) return 0;
        for(int j=i;j<=n+1;j++) swap(a[i][j],a[k][j]);
        for(int j=i;j<=n+1;j++) a[i][j]/=del;
        for(k=1;k<=n;k++) if(k!=i){
            del=a[k][i];
            for(int j=i;j<=n+1;j++) a[k][j]-=a[i][j]*del;
        }
    }
    return del;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
            for(int j=1;j<=n+1;j++) scanf("%lf",&a[i][j]);
    if(!gauss()) puts("No Solution");
    else for(int i=1;i<=n;i++) printf("%.2lf\n", a[i][n+1]);
}

明显我们可以看到，整个算法是$n^2$的，由于输入往往就是同一时间复杂度，所以不用寻求更快的方法。

8.prufer序列

Prufer数列是无根树的一种数列。在组合数学中，Prufer数列由有一个对于顶点标过号的树转化来的数列，点数为n的树转化来的Prufer数列长度为n-2。

性质：

1. prufer序列中某个编号出现的次数就等于这个编号的节点在无根树中的度数-1
2. 一棵n个节点的无根树唯一地对应了一个长度为n-2的数列，数列中的每个数都在1到n的范围内。
3. $n$个点的无向完全图的生成树的计数：$n^{n-2}$,即$n$个点的有标号无根树的计数
4. n个节点的度依次为$d_1,d_2,d_3,...,d_n$的无根树共有$\frac{(n-2)!}{\Pi_{i=1}^{n}(d_i-1)!}$个，因为此时Prufer编码中的数字i恰好出现$d_i-1$次，$(n-2)!$是总排列数。
5. n个点的有标号有根树的计数：$n^{(n-2)}*n=n^{n-1}$

9.BSGS

又被叫做拔山盖世算法。

作用：求$y^x\equiv z(mod\ p)$其中$(y,p)=1$

# include <bits/stdc++.h>
# define RG register
# define IL inline
# define Fill(a, b) memset(a, b, sizeof(a))
using namespace std;
typedef long long ll;
template <class Int>
IL void Input(RG Int &x){
    RG int z = 1; RG char c = getchar(); x = 0;
    for(; c < '0' || c > '9'; c = getchar()) z = c == '-' ? -1 : 1;
    for(; c >= '0' && c <= '9'; c = getchar()) x = (x << 1) + (x << 3) + (c ^ 48);
    x *= z;
}
IL void None(){
    puts("Orz, I cannot find x!");
}
int p;
IL int Pow(RG ll x, RG ll y){
    RG ll ret = 1;
    for(; y; x = x * x % p, y >>= 1)
        if(y & 1) ret = ret * x % p;
    return ret;
}
map <int, int> pw;
IL void BSGS(RG int x, RG int y){
    pw.clear();
    if(y == 1){
        puts("0");
        return;
    }
    RG int ans = -1, m = sqrt(p) + 1, xx, s = y;
    for(RG int i = 0; i < m; ++i){
        pw[s] = i;
        s = 1LL * s * x % p;
    }
    xx = Pow(x, m), s = 1;
    for(RG int i = 1; i <= m + 1; ++i){
        s = 1LL * s * xx % p;
        if(pw.count(s)){
            ans = i * m - pw[s];
            break;
        }
    }
    if(ans < 0) None();
    else printf("%d\n", ans);
}
int T, k, y, z;
int main(RG int argc, RG char* argv[]){
    for(Input(T), Input(k); T; --T){
        Input(y), Input(z), Input(p);
        if(k == 1) printf("%d\n", Pow(y, z));
        else if(k == 2){
            RG int d = (y % p) ? 1 : p;
            if(z % d) None();
            else printf("%lld\n", 1LL * Pow(y, p - 2) * z % p);
        }
        else{
            if(y % p) BSGS(y % p, z % p);
            else None();
        }
    }
    return 0;
}

10.斯特林数

一般用到的是第二类斯特林数，针对于放球模型。

（1）n个不同的球，放入m个无区别的盒子，不允许盒子为空。

方案数：$S(n,m)$。这个跟第二类Stirling数的定义一致。

（2）n个不同的球，放入m个有区别的盒子，不允许盒子为空。

方案数：$m!*S(n,m)$ 。因盒子有区别，乘上盒子的排列即可。

（3）n个不同的球，放入m个无区别的盒子，允许盒子为空。

方案数：$\sum_{k=0}^mS(n,k)$ 。枚举非空盒的数目便可。

（4）n个不同的球，放入m个有区别的盒子，允许盒子为空。

11.矩阵加速

矩阵加速可以把一些本来需要递推的加法式子优化为$log$级的复杂度。

具体来说就是使用矩阵乘法。

假设有一个矩阵$B=\begin{bmatrix} 1&&0 \\ 2&&1 \\1&&1 \end{bmatrix}$和一个矩阵$A=\begin{bmatrix} 1&&2&&3\\1&&2&&3 \end{bmatrix}$

这俩乘起来，得到一个$C=\begin{bmatrix} 1*1+2*2+1*3&&0*1+1*2+1*3\\1*1+2*2+1*3 && 0*1+1*2+1*3\end{bmatrix}$

公式化的话，就是对于一个$n$行$r$列的矩阵A和一个$r$行$m$列的矩阵B，其相乘得到的矩阵C，其$i$行$j$列的数$C[i][j]=\sum_{k=1}^rA_{i,r}B_{r,j}$

一个小例子就是斐波那契。

如果我们令矩阵A为$\begin{bmatrix} F_i&&F_{i-1}\end{bmatrix}$，令矩阵B为$\begin{bmatrix} 1&&1\\1&&0\end{bmatrix}$

这样我们得到的矩阵C显然为$\begin{bmatrix} F_i*1+F_{i-1}*1&&F_{i}*1\end{bmatrix}=\begin{bmatrix}F_{i+1}&&F_i\end{bmatrix}$

可以发现就相当于将斐波那契数列向前递推了一位。

矩阵乘法满足结合律，所以可以进行快速幂操作。

struct poo
{
    long long a[11][11];
};
poo m,ma,st;
long long n,p,k,T;
inline poo cheng(poo a,poo b)
{
    poo ans;
    memset(ans.a,0,sizeof(ans.a));
    for(re int i=1;i<=3;i++)
     for(re int j=1;j<=3;j++)
      for(re int k=1;k<=3;k++)
      {
        ans.a[i][j]=(ans.a[i][j]+a.a[i][k]*b.a[k][j]%mo)%mo;
      }
    return ans;
}
inline poo qmo(poo x)
{
    poo ans=st;
    while(n)
    {
        if(n&1)
        ans=cheng(ans,x);
        x=cheng(x,x);
        n>>=1;
    }
    return ans;
}
int main()
{
    cin>>T;
    m.a[1][3]=1;m.a[1][4]=0;m.a[1][3]=1;
    m.a[2][3]=1;m.a[2][5]=0;m.a[2][3]=0;
    m.a[3][4]=0;m.a[3][6]=1;m.a[3][3]=0;
    for(re int i=1;i<=3;i++)
    st.a[i][i]=1;
    while(T--)
    {
        cin>>n;
        n--;
        memset(ma.a,0,sizeof(ma.a));
        ma=qmo(m);
        cout<<ma.a[1][5]<<endl;
    }
}

对于其它题目，可以将乘法重载为矩阵乘法从而简化代码结构。

12.莫比乌斯反演

相当常用非常重要。

$\mu(x)$是莫比乌斯函数，有定义：$\sum_{d|x}\mu(d)=[x==1]$且有$\mu(1)=1$。

人话：

1. 当$d=1$时，$μ(d)=1$；
2. 当$d=\prod_{d=1}^kp_i$且$p_i$为互异素数时，$\mu(d)=(-1)^k$。(说直白点，就是$d$分解质因数后，没有幂次大于平方的质因子，此时函数值根据分解的个数决定)；
3. 只要当$d$含有任何质因子的幂次大于等于2，则函数值为0.

线筛，求：

void get_mu(int n)
{
    mu[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]){prim[++cnt]=i;mu[i]=-1;}
        for(int j=1;j<=cnt&&prim[j]*i<=n;j++)
        {
            vis[prim[j]*i]=1;
            if(i%prim[j]==0)break;
            else mu[i*prim[j]]=-mu[i];
        }
    }
 }

反演：

定义$f(n)$和$F(n)$为定义在自然数上的函数。并且满足：

$$F(n)=\sum_{d|n}f(n)$$

则有：

$$f(n)=\sum_{d|n}\mu(d)F(\lfloor\frac{n}{d}\rfloor)$$

证明：

$$\begin{aligned}\sum_{d|n}\mu(d)F(\lfloor\frac{n}{d}\rfloor)&=\sum_{d|n}\mu(d)\sum_{i|\lfloor\frac{n}{d}\rfloor}f(i)\\&=\sum_{i|n}f(i)\sum_{d|\lfloor\frac{n}{i}\rfloor}\mu(d)\\&=f(n)\end{aligned}$$

另有，给出限定$N$，如果有：

$$F(n)=\sum_{n|d}^Nf(d)$$

则能够推出

$$f(n)=\sum_{n|d}^N\mu(\frac{d}{n})F(d)$$

对于莫比乌斯函数有有趣的性质：

$$\sum_{d|n}\frac{\mu(d)}{d}=\frac{\varphi(n)}{n}$$

整除分块

求$\sum_{i=1}^n\lfloor\frac{n}{i}\rfloor$

for(int l=1,r;l<=n;l=r+1)
{
    r=n/(n/l);
    ans+=(r-l+1)*(n/l);
}

$\sqrt n$复杂度。

例子：

求：

$$Ans=\sum_{i=1}^n\sum_{j=1}^n[gcd(i,j)==prime]$$

直接算肯定不行，改成枚举质数

$$Ans=\sum_{d\in prime}\sum_{i=1}^n\sum_{j=1}^n[gcd(i,j)==d]$$

根据反演套路，设两个函数

$$f(d)=\sum_{i=1}^n\sum_{j=1}^m[gcd(i,j)==d]$$

$$F(n)=\sum_{n\mid d}f(d)=\lfloor \frac Nd \rfloor \lfloor \frac Md \rfloor$$
根据莫比乌斯反演可以得到：
$$f(n)=\sum_{n\mid d}\mu(\frac dn)F(d)$$
我们发现原式子后面的一坨就是$f(d)$

那么现在就是要求：

$$Ans=\sum_{d\in prime}f(d)=\sum_{d\in prime}\sum_{d\mid p}\mu(\frac pd)F(p)$$
然后把枚举p换成枚举$\frac pd$
$$=\sum_{d\in prime}\sum_{p=1}^{\frac nd}\mu(p)F(dp)=\sum_{d\in prime}\sum_{p=1}^{\frac nd}\mu(p)(\lfloor \frac {n}{dp} \rfloor)^2$$
这个$dp$不是很方便我们把它替换成$T$
$$Ans=\sum_{T=1}^{n}\sum_{t|T,t\in prime}\mu(\lfloor\frac{T}{t}\rfloor)(\lfloor\frac{n}{T}\rfloor)^2$$
$(\lfloor\frac{n}{T}\rfloor)^2$和$t$没关系，所以把它提出去
$$Ans=\sum_{T=1}^{n}(\lfloor\frac{n}{T}\rfloor)^2\sum_{t|T,t\in prime}\mu(\lfloor\frac{T}{t}\rfloor)$$
这样这个式子就可以在$O(n)$的复杂度内求出来了。

求：

$$Ans=\sum_{i=1}^{n}\sum_{j=1}^{m}gcd(i,j)^k$$

$$\begin{aligned} Ans&=\sum_{i=1}^{n}\sum_{j=1}^{m}gcd(i,j)^k\\ &=\sum_{d=1}^{min(n,m)}\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)=d]d^k\\ &=\sum_{d=1}^{min(n,m)}d^k\sum_{i=1}^{n}\sum_{j=1}^{m}[gcd(i,j)=d]\\ &=\sum_{d=1}^{min(n,m)}d^k\sum_{d\mid T}\mu(\frac{T}{d})\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor\\ &=\sum_{T=1}^{min(n,m)}\lfloor\frac{n}{T}\rfloor\lfloor\frac{m}{T}\rfloor\sum_{d\mid T}d^k\mu(\frac{T}{d}) \end{aligned}$$

13.杜教筛

杜教筛可以在非线性时间里求出一个积性函数的前缀和。

积性函数:

1. $\mu(n)$,莫比乌斯函数
2. $\phi(n)$，欧拉函数。
3. $d(n)$,约数个数。
4. $\sigma(n)$,约数和函数。
5. $\epsilon(n)$,元函数，其值为$\epsilon(n)=[n=1]$。
6. $id(n)$，单位函数，$id(n)=n$。
7. $I(n)$，恒等函数，$I(n)=1$。

狄利克雷卷积的式子：

假设我们现在有两个数论函数$f,g$，则这两个函数的卷积是$(f*g)(n)=\sum_{d\mid n}f(d)·g(\frac{n}{d})$后面的括号表示范围，一般不写的时候可以默认其为$n$。

可以推出狄利克雷卷积满足以下运算律

1. 交换律:$(f∗g=g∗f)$；
2. 结合律:$((f∗g)∗h=f∗(g∗h))$；
3. 分配律:$((f+g)∗h=f∗h+g∗h)$；

可以类比乘法运算律记忆。

现在我们要求一个积性函数$f$的前缀和，也就是$\sum_{i=1}^{n}f(i)$。

我们尝试构造两个积性函数使$h=f*g$

那么我们求一下$\sum_{i=1}^{n}h(i)$。

先记$Sum(n)$为$\sum_{i=1}^{n}f(i)$
则：

$$\sum_{i=1}^{n}h(i)=\sum_{i=1}^{n}\sum_{d\mid i}g(d)f(\frac{i}{d})$$
然后明显可以反过来枚举。
$$→\sum_{d=1}^{n}g(d)\sum_{d\mid i}f(\frac{i}{d})$$
改成枚举$\frac{i}{d}$
$$→\sum_{d=1}^{n}g(d)\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}f(i)=\sum_{d=1}^{n}g(d)S(\lfloor\frac{n}{d}\rfloor)$$
然后把式子的第一项提出来，整个代回去。
$$\sum_{i=1}^{n}h(i)=g(1)·S(n)+\sum_{d=2}^{n}g(d)·S(\lfloor\frac{n}{d}\rfloor)$$
移项
$$g(1)·S(n)=\sum_{i=1}^{n}h(i)-\sum_{d=2}^{n}g(d)·S(\lfloor\frac{n}{d}\rfloor)$$
这样$g(1)$明显为$1$，所以这个式子就很明显了，只要$h(i)$的前缀和好求那么这个式子就可以在非线性时间里求出来了。

因为$h=f*g$我们换个形式表示上面的式子。

$$→g(1)·S(n)=\sum_{i=1}^{n}(f*g)(i)-\sum_{d=2}^{n}g(d)·S(\lfloor\frac{n}{d}\rfloor)$$
所以只要找到一个合适的$g$就行了。

看个例子，我们这个题要求啥来着，$\sum_{i=1}^{n}\mu(i)$和$\sum_{i=1}^{n}\varphi(i)$

先看第一个。

就不推了，根据上面那个把$f$换成$\mu$直接代到最后面。

那么应该怎么给$g$取值呢，我们可以简明扼要的先看一下那一项变成什么了。

$$→\sum_{i=1}^{n}(\mu*g)(i)$$
我们知道$\mu*I=\epsilon$。那么可以把上面的式子看成
$$\sum_{i=1}^{n}(\mu*I)(i)=\sum_{i=1}^{n}\epsilon(i)$$
元函数的前缀和就非常好求，就是$1$，所以我们求的答案
$$S(n)=1-\sum_{d=2}^{n}g(d)·S(\lfloor\frac{n}{d}\rfloor)$$
再看第二个，我们还是相同的直接把$\varphi$代到最后面去。

则我们有式子

$$\sum_{i=1}^{n}(\varphi*g)(i)$$
思考一下，我们记得欧拉函数有个有趣的性质$\sum_{d|n}\varphi(d)=n$

我们把它用卷积的形式表达，就是$\varphi*I=id$

带入刚才的式子里面。

$$\sum_{i=1}^{n}(\varphi*g)(i)=\sum_{i=1}^{n}id(i)$$

#include <bits/stdc++.h>
#include <tr1/unordered_map>
using namespace std;
const int MAXN=4e6+7;
const int M=4e6;
#define ll long long 
bool vis[MAXN];
int mu[MAXN],sum1[MAXN];
ll phi[MAXN],sum2[MAXN];
int cnt,prime[MAXN];
tr1::unordered_map<ll,ll> w1;
tr1::unordered_map<int,short> w;
inline void get(int N)
{
    phi[1]=mu[1]=1;
    for(int i=2;i<=N;i++){
        if(!vis[i]){
            prime[++prime[0]]=i;
            mu[i]=-1;
            phi[i]=i-1;
        }
        for(int j=1;j<=prime[0];j++){
            if(i*prime[j]>N) break;
            vis[i*prime[j]]=1;
            if(i%prime[j]==0){
                phi[i*prime[j]]=phi[i]*prime[j];
                break;
            } else mu[i*prime[j]]=-mu[i],phi[i*prime[j]]=phi[i]*(prime[j]-1);
        }
    }
    for(int i=1;i<=N;i++) sum1[i]=sum1[i-1]+mu[i],sum2[i]=sum2[i-1]+phi[i];
}
int djsmu(int x)
{
    if(x<=M) return sum1[x];
    if(w[x]) return w[x];
    int ans=1;
    for(int l=2,r;l<=x;l=r+1){
        if(r==2147483647) break;
        r=x/(x/l);
        ans-=(r-l+1)*djsmu(x/l);
    }
    return w[x]=ans;
}
ll djsphi(int x)
{
    if(x<=M) return sum2[x];
    if(w1[x]) return w1[x];
    ll ans=1ll*x*(1ll*x+1)/2;
    for(int l=2,r;l<=x&&l>=0;l=r+1){
        if(r==2147483647) break;
        r=x/(x/l);
        ans-=1ll*(r-l+1)*djsphi(x/l);
    }
    return w1[x]=ans;
}
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    while(ch=='-')c*=-1,ch=getchar();
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
int main()
{
    int T=read();
    get(M);
    while(T--){
        int n;
        n=read();
        printf("%lld %d\n", djsphi(n),djsmu(n));
    }
}

14.FFT

解决的问题主要是多项式相乘。有时候还可以解决其他问题。

容易知道的是：对于任意一个多项式$y(x)=a_0x^n+a_1x^{n-1}+...+a_{n-1}x+a_n$,其与另一个多项式$f(x)=b_0x^n+b_1x^{n-1}+...+b_{n-1}x+b_n$进行多项式相乘的时候，由于每项对应相乘，导致相乘的过程中进行了$n^2$数量级的运算。

可以考虑一种方法加速这个运算。

引入多项式的点值表达法。

一个次数界为$n$的多项式的点值表达是由n个点值所组成的集合(可以看作n个点决定一个n次多项式)

$$\{(x_0,y_0),(x_1,y_1),...,(x_{n-1},y_{n-1})\}$$

则对于上述多项式$y(x)$，用点值表示可以是上面的形式。

对于多项式$f(X)$，如此进行表示

$$\{(x_0,y^{'}_0),(x_1,y^{'}_1),...,(x_{n-1},y^{'}_{n-1})\}$$

容易考虑的是，二者相加得出的新多项式的点值表示是：

$$\{(x_0,y_0+y^{'}_0),(x_1,y_1+y^{'}_1),...,(x_{n-1},y_{n-1}+y^{'}_{n-1})\}$$

可以看作是两个函数相加之后找到对应的点。

根据上面的（(可以看作n个点决定一个n次多项式)），我们可以思考，如若两个多项式进行相乘，则最高次幂为$x^{2n}$，则这个多项式一定可以有点值表示法仅使用2n个点表示。

令相乘得到的新多项式为$C(x)$，则有$C(x)=y(x)f(x)$。容易知道，对于任意一个$x_k$,都可以有$C(x_k)=y(x_k)f(x_k)$。

则直接将二者点值表达式中的行变量（即y）相乘即可的到新的点值表达式。

问题在于$C(x)$需要2n个点来确定，所以要在表示$f(x)$和$y(x)$的时候进行拓展，将其拓展为2n项。

例如$y(x)=\{(x_0,y_0),(x_1,y_1),...,(x_{n-1},y_{n-1}),...,(x_{2n-1},y_{2n-1})\}$

则$C(x)=\{(x_0,y_0y^{'}_0),(x_1,y_1y^{'}_1),...,(x_{n-1},y_{n-1}y^{'}_{n-1}),...,(x_{2n-1},y_{2n-1}y^{'}_{2n-1})\}$

这样就可以在$O(n)$的时间复杂度内将两个多项式相乘。

然后问题在于如何选择点使多项式在转换成点值表达式的时候能有更快的速度。明显对于一般的选点，每个点都要进行n次运算。考虑使用单位复数根来加速运算。即利用FFT和DFFT加速。

对于复数，上过高中的各位应该都知道，我们定义$i=\sqrt{-1}$，用$a+bi$表示一个复数。

对于一个复数，可以把复数看成复平面直角坐标系上的一个点。

盗别人一个图，

对于复数，可以进行一些运算。

例如给出两个复数$a_1+b_1i,a_2+b_2i$，二者可以进行加减运算。具体运算方法可以将其看成两个多项式相乘。

复数相加满足平行四边形法则。

另外的，如果我们将一个复数看成是由模长和极角表示，即将其表示为$(d,\theta)$，则对于如此表示的两个复数相乘得出的结果为$(d1d2,\theta_1+\theta_2)$。这个性质很重要。

定义复数的指数形式为：

$$e^{iu}=cos(u)+isin(u)$$

我们定义复数单位根为：

$$\omega_n^k=cos\frac{k}{n}2\pi+isin\frac{k}{n}2\pi （1）$$

另有

$$\omega_n=e^{2\pi i/n}(2)$$

经过转化可以转化为类似(1)式的形式。

如果我们对这种复数进行极坐标表示的话，它们都可以表示为$(1,\theta)$

容易得出$(\omega_n^1)^k=\omega_n^k$

另外还有一些性质：

$\huge1.\omega_n^k=\omega_{2n}^{2k}$

明显：$\omega_n^k=cos\frac{k}{n}2\pi+isin\frac{k}{n}2\pi=cos\frac{2k}{2n}2\pi+isin\frac{2k}{2n}2\pi=\omega_{2n}^{2k}$

$\huge2.\omega_n^k=-\omega_n^{k+\frac{\pi}{2}}$

首先考虑，$\omega_n^{2/n}=\omega_2=-1(3)$

$\omega_n^{2/n}=cos\frac{2/n}{n}2\pi+isin\frac{2/n}n2\pi=cos\frac122\pi+isin\frac122\pi=cos\pi+isin\pi=\omega_2=-1$

则有$\omega_n^{k+2/n}=\omega_n^k\omega_n^{2/n}=-\omega_n^k$

然后证明$(\omega_n^{k+2/n})^2=(\omega_n^k)^2$

$(\omega_n^{k+2/n})^2=\omega_n^{2k+n}=\omega_n^{2k}\omega_n^n=\omega_n^{2k}=(\omega_n^k)^2$

然后可以考虑DFT的问题。

明显我们是想把一个多项式$A(x)=\sum_{i=1}^{n}a_ix^i$里面求出n个点来让它能够使用点值表达的形式。

但是暴力的去找还是 $n^2$ 的。

不妨把$A(x)$展开以观察它的性质。

则有$A(x)=a_0+a_1x^1+...+a_{n-1}x^{n-1}$

可以将其利用奇偶性分开。

$A(X)=(a_0+a_2x^2+...+a_{n-2}x^{n-2})+(a_1x^1+a_3x^3+...a_{n-1}x^{n-1})=(a_0+a_2x^2+...+a_{n-2}x^{n-2})+x(a_0+a_2x^2+...+a_{n-2}x^{n-2})$

明显可以分为前后两个部分。

考虑转化$A_1(x)$以及$A_2(x)$使其能与$A(x)$有相同的形式，则代换$x$为$x^2$

则有$A_1(x)=a_0+a_2x+a_4x^2+...+a_{n-2}x^{\frac n2-1}$

$A_2(x)=a_1+a_3x+a_5x^2+...+a_{n-2}x^{\frac n2-1}$

$A(x)=A_1(x^2)+xA_2(x^2)$

明显的是，对于$A_1(x)$以及$A_2(x)$，我们可以继续对其进行上述操作使其继续分割下去。

接着我们利用单位根的性质，考虑将$\omega_n^k$代入。

则$A(\omega_n^k)=A_1((\omega_n^k)^2)+\omega_n^k A_2((\omega_n^k)^2)$

$=A_1(\omega_n^{2k})+\omega_n^kA_2(\omega_n^{2k})$

$=A_1(\omega_{\frac n2}^k)+\omega_n^kA_2(\omega_{\frac n2}^k)$

接着考虑将$\omega_n^{k+\frac n2}$代入

可得$A(\omega_n^{k+\frac n2})=A_1(\omega_{\frac n2}^k)-\omega_n^kA_2(\omega_{\frac n2}^k)$

发现二者只有第二项的符号有所不同，可以分治计算。

剩下的大可以不讲。

四、数据结构

1.线段树

拿以前的板子凑一凑，也没大有啥说的。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#define re register
#define maxn 1000007
#define ll long long
#define lz rt<<1
#define rz rt<<1|1
using namespace std;
ll a[maxn<<2],n,m,x,y,k,p,flag;
struct tree
{
    long long v,mul,add;
};
tree st[maxn<<2];
inline long long read()
{
    long long x=0,c=1;
    char ch=' ';
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    while(ch=='-')c*=-1,ch=getchar();
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
inline void pushup(int rt)
{
    st[rt].v=(st[lz].v+st[rz].v)%p;
}
inline void build(ll l,ll r,ll rt)
{
    st[rt].mul=1;
    if(l==r)
    st[rt].v=a[l];
    else
    {
        int m=r+l>>1;
        build(l,m,lz);
        build(m+1,r,rz);
        pushup(rt);
    }
    st[rt].v%=p;
}
inline void pushdown(ll l,ll r ,ll rt)
{
    ll m=l+r>>1;
    if(st[rt].mul!=1)
    {
        st[lz].mul=(st[lz].mul*st[rt].mul)%p;
        st[rz].mul=(st[rz].mul*st[rt].mul)%p;
        st[lz].add=(st[lz].add*st[rt].mul)%p;
        st[rz].add=(st[rz].add*st[rt].mul)%p;
        st[lz].v=(st[lz].v*st[rt].mul)%p;
        st[rz].v=st[rz].v*st[rt].mul%p;
        st[rt].mul=1;
    }
    if(st[rt].add!=0)
    {
        st[lz].add=(st[lz].add+st[rt].add)%p;
        st[rz].add=(st[rz].add+st[rt].add)%p;
        st[lz].v=(st[lz].v+(m-l+1)*st[rt].add)%p;
        st[rz].v=(st[rz].v+(r-m)*st[rt].add)%p;
        st[rt].add=0;
    }
}
inline void update1(ll L,ll R,ll c,ll l,ll r,ll rt)
{
    if(r<L||l>R)
    return;
    if(L<=l&&r<=R)
    {
        st[rt].v=st[rt].v*c%p;
        st[rt].mul=st[rt].mul*c%p;
        st[rt].add=st[rt].add*c%p;
        return;
    }
    pushdown(l,r,rt);
    ll m=l+r>>1;
    if(L<=m)
    update1(L,R,c,l,m,lz);
    if(R>m)
    update1(L,R,c,m+1,r,rz);
    pushup(rt);
}
inline void update2(ll L,ll R,ll c,ll l,ll r,ll rt)
{
    if(r<L||l>R)
    return;
    if(L<=l&&r<=R)
    {
        st[rt].v=(st[rt].v+c*(r-l+1))%p;
        st[rt].add=(st[rt].add+c)%p;
        return;
    }
    pushdown(l,r,rt);
    ll m=l+r>>1;
    if(L<=m)
    update2(L,R,c,l,m,lz);
    if(R>m)
    update2(L,R,c,m+1,r,rz);
    pushup(rt);
}
inline ll query(ll L,ll R,ll l,ll r,ll rt)
{
    if(L<=l&&r<=R)
    return st[rt].v;
    ll m=l+r>>1;
    pushdown(l,r,rt);
    ll ans=0;
    if(L<=m)
    ans+=query(L,R,l,m,lz);
    if(R>m)
    ans+=query(L,R,m+1,r,rz);
    return ans;
}
int main()
{
    n=read();m=read();p=read();
    for(re int i=1;i<=n;i++)
    a[i]=read();
    build(1,n,1);
    for(re int i=1;i<=m;i++)
    {
        flag=read();x=read();y=read();
        if(flag==1)
        {
            k=read();
            update1(x,y,k,1,n,1);
        }else
        if(flag==2)
        {
            k=read();
            update2(x,y,k,1,n,1);
        }else
        cout<<query(x,y,1,n,1)%p<<endl;
    }
}

1.1 可持久化线段树

具体来讲，就是：

一个线段树，支持:

1.在某个历史版本上修改某一个位置上的值
2.访问某个历史版本上的某一位置的值

以前还画过图来着。

就小问题，空间开32倍。

#include <bits/stdc++.h>
using namespace std;
#define mid (l+r>>1)
const int MAXN=1e6+7;
int n,m,size,a[MAXN];
int L[MAXN<<5],R[MAXN<<5],T[MAXN],st[MAXN<<5],q;
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    while(ch=='-')c*=-1,ch=getchar();
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
inline int build(int l,int r)
{
    int rt=++size;
    if(l==r){
        st[rt]=a[l];
        return rt;
    }
    L[rt]=build(l,mid);
    R[rt]=build(mid+1,r);
    return rt;
}
inline int update(int pre,int l,int r,int x,int k)
{
    int rt=++size;
    if(l==r){
        st[rt]=k;
        return rt;
    }
    L[rt]=L[pre];R[rt]=R[pre];
    if(mid>=x) L[rt]=update(L[pre],l,mid,x,k);
    else R[rt]=update(R[pre],mid+1,r,x,k);
    return rt;
}
inline int query(int v,int l,int r,int x)
{
    if(l==r) return st[v];
    if(x<=mid) return query(L[v],l,mid,x);
    else return query(R[v],mid+1,r,x);
}
int main()
{
    n=read();q=read();
    for(int i=1;i<=n;i++) a[i]=read();
    T[0]=build(1,n);
    for(int i=1;i<=q;i++){
        int v,f,x,k;
        v=read();f=read();
        if(f==1){
            x=read();k=read();
            T[i]=update(T[v],1,n,x,k);
        } else {
            x=read();
            T[i]=T[v];
            printf("%d\n",query(T[v],1,n,x));
        }
    }
}

1.2 主席树

作用和上面那个差不多，就是要支持静态区间第k大。

就是对每个节点都给他搞一个新的线段树，然后求的时候利用前缀和的思想。

#include <bits/stdc++.h>
using namespace std;
#define mid (l+r>>1)
const int MAXN=2e5+7;
int n,m,size;
struct Node
{
    int l,r,sum;
}st[MAXN<<6];
int root[MAXN],rank[MAXN],L[MAXN<<6],R[MAXN<<6],sum[MAXN<<6],a[MAXN],b[MAXN],q,T[MAXN];
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    while(ch=='-')c*=-1,ch=getchar();
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
inline int build(int l,int r)
{
    int rt=++size;
    sum[rt]=0;
    if(l<r){
        L[rt]=build(l,mid);
        R[rt]=build(mid+1,r);
    }
    return rt;
}
inline int update(int pre,int l,int r,int x)
{
    int rt=++size;
    L[rt]=L[pre];R[rt]=R[pre];sum[rt]=sum[pre]+1;
    if(l<r){
        if(x<=mid) L[rt]=update(L[pre],l,mid,x);
        else R[rt]=update(R[pre],mid+1,r,x);
    }
    return rt;
}
inline int query(int u,int v,int l,int r,int k)
{
    if(l>=r) return l;
    int x=sum[L[v]]-sum[L[u]];
    if(x>=k) return query(L[u],L[v],l,mid,k);
    else return query(R[u],R[v],mid+1,r,k-x);
}
int main()
{
    n=read();q=read();
    for(int i=1;i<=n;i++) a[i]=b[i]=read();
    sort(b+1,b+n+1);
    m=unique(b+1,b+n+1)-b-1;
    T[0]=build(1,m);
    for(int i=1;i<=n;i++){
        int t=lower_bound(b+1,b+m+1,a[i])-b;
        T[i]=update(T[i-1],1,m,t);
    }
    while(q--){
        int x,y,k;
        x=read();y=read();k=read();
        int t=query(T[x-1],T[y],1,m,k);
        printf("%d\n", b[t]);
    }
}

用的时候写不出来就很尴尬。

1.3 树套树

简单来说，就是：

1.查询k在区间内的排名
2.查询区间内排名为k的值
3.修改某一位值上的数值

平衡树做不了。

然后就是搞一个树状数组套动态开点的权值线段树。

#include <bits/stdc++.h>
using namespace std;
const int MAXN=1e5+7;
#define mid ((l+r)>>1)
const int inf=2147483647;
struct po
{
    int l,r,k;
    int f;
    int pos,t;
}q[MAXN];
int a[MAXN],size,cnt[3],L[MAXN<<6],R[MAXN<<6],T[MAXN],b[MAXN<<1];
int st[MAXN<<6],n,t,totx,toty,xx[MAXN],yy[MAXN],m,num;
inline char gc(){
    static char BUFF[1000000],*S=BUFF,*T=BUFF;
    return S==T&&(T=(S=BUFF)+fread(BUFF,1,1000000,stdin),S==T)?EOF:*S++;
}
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch>'9'||ch<'0')&&ch!='-')ch=gc();
    while(ch=='-')c*=-1,ch=gc();
    while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=gc();
    return x*c;
}
inline void get_lson()
{
    for(int i=1;i<=totx;i++) xx[i]=L[xx[i]];
    for(int i=1;i<=toty;i++) yy[i]=L[yy[i]];
}
inline void get_rson()
{
    for(int i=1;i<=totx;i++) xx[i]=R[xx[i]];
    for(int i=1;i<=toty;i++) yy[i]=R[yy[i]];
}
inline void get_T(int x)
{
    totx=toty=0;
    for(int i=q[x].l-1;i;i-=i&(-i)) xx[++totx]=T[i];
    for(int i=q[x].r;i;i-=i&(-i)) yy[++toty]=T[i];
}
int update(int pre,int l,int r,int k,int x)
{
    int rt=pre;
    if(!pre) rt=++size;
    L[rt]=L[pre],R[rt]=R[pre],st[rt]=st[pre]+x;
    if(l==r) return rt;
    if(k<=mid) L[rt]=update(L[pre],l,mid,k,x);
    else R[rt]=update(R[pre],mid+1,r,k,x);
    return rt;
}
inline void add(int x,int val)
{
    int d=lower_bound(b+1,b+t+1,a[x])-b;
    for(int i=x;i<=n;i+=(i&-i)) T[i]=update(T[i],1,t,d,val);
}
int find(int l,int r,int k)
{
    if(l==r) return 0;
    if(k<=mid){
        get_lson();
        return find(l,mid,k);
    } else {
        int sum=0;
        for(int i=1;i<=totx;i++) sum-=st[L[xx[i]]];
        for(int i=1;i<=toty;i++) sum+=st[L[yy[i]]];
        get_rson();
        return sum+find(mid+1,r,k);
    }
}
int findx(int l,int r,int k)
{
    if(l==r) return l;
    int sum=0;
    for(int i=1;i<=totx;i++) sum-=st[L[xx[i]]];
    for(int i=1;i<=toty;i++) sum+=st[L[yy[i]]];
    if(k<=sum){
        get_lson();
        return findx(l,mid,k);
    } else {
        get_rson();
        return findx(mid+1,r,k-sum);
    }
}
int findt(int l,int r,int k)
{
    int sum=0;
    if(l==r){
        for(int i=1;i<=totx;i++) sum-=st[xx[i]];
        for(int i=1;i<=toty;i++) sum+=st[yy[i]];
        return sum;
    }
    if(k<=mid){
        get_lson();
        return findt(l,mid,k);
    } else {
        get_rson();
        return findt(mid+1,r,k);
    }
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++) a[i]=read(),b[++num]=a[i];
    for(int i=1;i<=m;i++){
        int f=read();q[i].f=f;
        if(f==3){
            q[i].pos=read();q[i].k=read();b[++num]=q[i].k;
        } else {
            q[i].l=read();q[i].r=read();q[i].k=read();
            if(f!=2) b[++num]=q[i].k;
        }
    }
    b[++num]=inf;
    sort(b+1,b+num+1);
    t=unique(b+1,b+num+1)-b-1;
    for(int i=1;i<=n;i++) add(i,1);
    for(int i=1;i<=m;i++){
        if(q[i].f==1){
            get_T(i);
            int d=lower_bound(b+1,b+t+1,q[i].k)-b;
            printf("%d\n", find(1,t,d)+1);
        } else if(q[i].f==2){
            get_T(i);
            printf("%d\n", b[findx(1,t,q[i].k)]);
        } else if(q[i].f==3){
            add(q[i].pos,-1);a[q[i].pos]=q[i].k;add(q[i].pos,1);
        } else if(q[i].f==4){
            int f=lower_bound(b+1,b+t+1,q[i].k)-b;
            get_T(i); int d=find(1,t,f);
            if(d==0) printf("-2147483647\n");
            else {
                get_T(i);
                printf("%d\n", b[findx(1,t,d)]);
            }
        } else {
            int f=lower_bound(b+1,b+t+1,q[i].k)-b;
            get_T(i);
            int d=find(1,t,f);get_T(i);
            d+=findt(1,t,f);get_T(i);
//          int dd=find(1,t,t);get_T(i);
//          dd+=findt(1,t,t);
            if(d==find(1,t,t)) printf("2147483647\n");
            else {
                get_T(i);
                printf("%d\n", b[findx(1,t,d+1)]);
            }
        }
    }
}

没法活学活用。

1.4可持久化平衡树

正解打不出来。

用上面的方法去过的。

具体来说：
1、 插入 x

2、 删除 x（若有多个相同的数，应只删除一个，如果没有请忽略该操作）

3、 查询 x 的排名（排名定义为比当前数小的数的个数 +1）

4、查询排名为 x 的数

5、 求 x 的前驱（前驱定义为小于 x，且最大的数，如不存在输出 $-2^{31}+1$ ）

6、求 x 的后继（后继定义为大于 x，且最小的数，如不存在输出 $2^{31}-1$ ）

#include <bits/stdc++.h>
#define mid (((r+l)>>1))
using namespace std;
const int MAXN=5e5+7;
const int inf=2147483647;
int L[MAXN*45],R[MAXN*45],T[MAXN],st[MAXN*45];
int n,m,ll=-inf,rr=inf,size=1,del;
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    while(ch=='-')c*=-1,ch=getchar();
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
int add_rt(int pre,int l,int r,int x)
{
    int rt=++size;
    L[rt]=L[pre];R[rt]=R[pre];st[rt]=st[pre];
    if(l==r){
        if(!(st[rt]==0&&del<0)) st[rt]+=del;
        return rt;
    }
    if(x<=mid) L[rt]=add_rt(L[pre],l,mid,x);
    else R[rt]=add_rt(R[pre],mid+1,r,x);
    st[rt]=0;
    if(L[rt]) st[rt]+=st[L[rt]];
    if(R[rt]) st[rt]+=st[R[rt]];
    return rt;
}
int query(int v,int l,int r,int x)
{
    if(l==r) return 0; if(v==0) return 0;
    if(x<=mid) return query(L[v],l,mid,x);
    else return (L[v]?st[L[v]]:0)+query(R[v],mid+1,r,x);
}
int findx(int v,int l,int r,int k)
{
    if(l==r) return l;
    int x=L[v]?st[L[v]]:0;
    if(x>=k) return findx(L[v],l,mid,k);
    else return findx(R[v],mid+1,r,k-x);
}
int findt(int v,int l,int r,int x)
{
    if(v==0) return 0;
    if(l==r) return st[v];
    if(x<=mid) return findt(L[v],l,mid,x);
    else return findt(R[v],mid+1,r,x);
}
int pre(int v,int l,int r,int x)
{
    int t=query(v,l,r,x);
    if(t==0) return -inf;
    return findx(v,l,r,t);
}
int nxt(int v,int l,int r,int x)
{
    int t=query(v,l,r,x)+findt(v,l,r,x);
    if(t==query(v,l,r,inf)) return inf;
    return findx(v,l,r,t+1);
}
int main()
{
    n=read();
    T[0]=1;
    for(int i=1;i<=n;i++){
        int v,f,x;
        v=read();f=read();x=read();
        if(f==1) del=1,T[i]=add_rt(T[v],ll,rr,x);
        if(f==2) del=-1,T[i]=add_rt(T[v],ll,rr,x);
        if(f==3) T[i]=T[v],printf("%d\n", query(T[v],ll,rr,x)+1);
        if(f==4) T[i]=T[v],printf("%d\n", findx(T[v],ll,rr,x));
        if(f==5) T[i]=T[v],printf("%d\n", pre(T[v],ll,rr,x));
        if(f==6) T[i]=T[v],printf("%d\n", nxt(T[v],ll,rr,x));
    }
}

2.平衡树

具体来说，就是上面那个题去掉可持久化。

我个人是比较喜欢splay

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<queue>
#define re register
#define maxn 5000007
#define ll long long
using namespace std;
int ch[maxn][7],f[maxn],cnt[maxn],key[maxn],size[maxn],mark[maxn],root,sz,data[maxn];
inline int read()
{
    int x=0,c=1; char cc=' ';
    while((cc<'0'||cc>'9')&&cc!='-') cc=getchar();
    while(cc=='-') c*=-1,cc=getchar();
    while(cc>='0'&&cc<='9') x=x*10+cc-'0',cc=getchar();
    return x*c;
}
inline int get(int x){return ch[f[x]][3]==x;}
inline void update(int x)
{
    if(x){
        size[x]=cnt[x];
        if(ch[x][0]) size[x]+=size[ch[x][0]];
        if(ch[x][4]) size[x]+=size[ch[x][5]];
    }
}
inline void clear(int x){ch[x][0]=ch[x][6]=size[x]=cnt[x]=key[x]=f[x]=0;}
inline void rotate(int x){
    int y=f[x],z=f[y];
    int kind=get(x);
    ch[y][kind]=ch[x][!kind];
    f[ch[y][kind]]=y;
    f[y]=x;ch[x][!kind]=y;f[x]=z;
    if(z) ch[z][ch[z][7]==y]=x;
    update(x);update(y);
}
inline void splay(int x)
{
    for(int fa;(fa=f[x]);rotate(x))
        if(f[fa]) rotate(get(x)==get(f[x])?fa:x);
    root=x;
}
inline void insert(int v)
{
    if(root==0){
        sz++;ch[sz][0]=ch[sz][8]=f[sz]=0;
        key[sz]=v;size[sz]=cnt[sz]=1;root=sz;return;
    }
    int now=root,fa=0;
    while(1){
        if(key[now]==v){
            cnt[now]++;
            update(now);update(fa);
            splay(now);break;
        }
        fa=now;now=ch[now][key[now]<v];
        if(now==0){
            sz++;
            ch[sz][0]=ch[sz][9]=0;key[sz]=v;
            size[sz]=1;cnt[sz]=1;f[sz]=fa;
            ch[fa][key[fa]<v]=sz;
            update(fa); splay(sz);
            break;
        }
    }
}
inline int find(int v)
{
    int ans=0,now=root;
    while(1){
        if(v<key[now]) now=ch[now][0];
        else {
            ans+=(ch[now][0]?size[ch[now][0]]:0);
            if(v==key[now]){
                splay(now);
                return ans+1;
            }
            ans+=cnt[now];
            now=ch[now][10];
        }
    }
}
inline int findx(int x)
{
    int now=root;
    while(1){
        if(ch[now][0]&&x<=size[ch[now][0]]) now=ch[now][0];
        else {
            int temp=(ch[now][0]?size[ch[now][0]]:0)+cnt[now];
            if(x<=temp) return key[now];
            x-=temp;now=ch[now][11];
        }
    }
}
inline int pre()
{
    int now=ch[root][0];
    while(ch[now][12]) now=ch[now][13];
    return now;
}
inline int next()
{
    int now=ch[root][14];
    while(ch[now][0]) now=ch[now][0];
    return now;
}
inline void del(int x)
{
    int xjbz=find(x);
    if(cnt[root]>1){
        cnt[root]--; return;
    }
    if(!ch[root][0]&&!ch[root][15]){
        clear(root);root=0;return;
    }
    if(!ch[root][0]){
        int y=root;
        root=ch[root][16]; f[root]=0;
        clear(y); return;
    } else if(!ch[root][17]){
        int y=root;
        root=ch[root][0]; f[root]=0;
        clear(y); return;
    } else {
        int leftbig=pre(),y=root;
        splay(leftbig);
        ch[root][18]=ch[y][19];
        f[ch[y][20]]=leftbig;
        clear(y);update(root);
        return;
    }
}
int main()
{
    int n,flag=0,x;
    n=read();
    for(re int i=1;i<=n;i++){
        flag=read();x=read();
        if(flag==1){
            insert(x);
        }else if(flag==2){
            del(x);
        }else if (flag==3)
        {
            printf("%d\n",find(x));
        }else if (flag==4)
        {
            printf("%d\n",findx(x));
        }else if (flag==5)
        {
            insert(x);
            printf("%d\n",key[pre()]);
            del(x);
        }else
        {
            insert(x);
            printf("%d\n",key[next()]);
            del(x);
        }
    }
    return 0;
}

3.动态树

Link cut Tree

听名字就比较容易想到干啥的。

支持删边连边，不过不大支持弄成一张图。要忽略掉已经相连的边的贡献，或者在联通时不进行链接。所以没办法完成一般的图论题目。但是很多树上的题目可以用它完成并且取得较为优秀的复杂度。

比如支持一下链求异或和以及单点修改。

动态树有相当大的灵活性以及相当高的独立性。所以适于结构体封装。

其它例子是对一个图不断加边，并且求两点桥的数量。图中包含重边自环

可以发现的是满足两点已经联通时可以不进行链接这一要求，转而讲两点间边的贡献归零达到这种操作的目的。其它方法显然是不很可行或者复杂度比较高的。

但是由于树链剖分的出奇小的常数也可以通过此题。

#include <bits/stdc++.h>
using namespace std;
#define lc ch[x][0]
#define rc ch[x][21]
const int MAXN=3e5+7;
int f[MAXN],ch[MAXN][8],s[MAXN],st[MAXN];
int r[MAXN],v[MAXN];
int n,m;
inline int read()
{
    int x=0,c=1;
    char ch=' ';
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    while(ch=='-')c*=-1,ch=getchar();
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*c;
}
inline bool nroot(int x){return ch[f[x]][0]==x||ch[f[x]][22]==x;}
inline void pushup(int x){s[x]=s[lc]^s[rc]^v[x];}
inline void pushr(int x){int t=lc;lc=rc;rc=t;r[x]^=1;} 
inline void pushdown(int x)
{
    if(r[x]){
        if(lc) pushr(lc);
        if(rc) pushr(rc);
        r[x]=0;
    }
}
inline void rotate(int x)
{
    int y=f[x],z=f[y],kind=ch[y][23]==x,w=ch[x][!kind];
    if(nroot(y)) ch[z][ch[z][24]==y]=x;ch[x][!kind]=y;ch[y][kind]=w;
    if(w)f[w]=y;f[y]=x;f[x]=z;
    pushup(y);
}
inline void splay(int x)
{
    int y=x,z=0;
    st[++z]=y;
    while(nroot(y)) st[++z]=y=f[y];
    while(z) pushdown(st[z--]);
    while(nroot(x)){
        y=f[x];z=f[y];
        if(nroot(y))
            rotate((ch[y][0]==x)^(ch[z][0]==y)?x:y);
        rotate(x);
    }
    pushup(x);
}
inline void access(int x)
{
    for(int y=0;x;x=f[y=x])
        splay(x),rc=y,pushup(x);
}
inline void makeroot(int x)
{
    access(x);splay(x);
    pushr(x);
}
inline int findroot(int x)
{
    access(x);splay(x);
    while(lc) pushdown(x),x=lc;
    splay(x);
    return x;
}
inline void split(int x,int y)
{
    makeroot(x);
    access(y);splay(y);
}
inline void link(int x,int y)
{
    makeroot(x);
    if(findroot(y)!=x) f[x]=y;
}
inline void cut(int x,int y)
{
    makeroot(x);
    if(findroot(y)==x&&f[y]==x&&!ch[y][0]){
        f[y]=ch[x][25]=0;
        pushup(x);
    }
}
int main()
{
    n=read();m=read();
    for(int i=1;i<=n;i++) v[i]=read();
    while(m--){
        int t=read(),x=read(),y=read();
        if(t==0) split(x,y),printf("%d\n", s[y]);
        if(t==1) link(x,y);
        if(t==2) cut(x,y);
        if(t==3) splay(x),v[x]=y;
    }
}

4.分块

不说啥了，这玩意就是暴力数据结构。

#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+7;
#define ll long long
ll a[MAXN],b[MAXN],belong[MAXN],l[MAXN],r[MAXN],block,minn[MAXN],tag[MAXN],ans;
ll n,m,t;
struct point{
    int x;
}q[MAXN];
inline int find_dis()
{
    ll p=0,minnn=1000000000000000ll;
    for(int i=1;i<=belong[m];i++) minnn=min(minnn,minn[i]+tag[i]);
    for(int i=1;i<=belong[m];i++){
        if(minn[i]+tag[i]==minnn){
            for(int j=l[i];j<=r[i];j++){
                if(b[j]+tag[i]==minnn){
                    q[++t].x=j;
                }
            }
        }
    }
    return minnn;
}
inline void change(int val)
{
    for(int k=1;k<=t;k++){
        if(belong[q[k-1].x]==belong[q[k].x]) continue;
        for(int i=belong[q[k-1].x]+1;i<belong[q[k].x];i++) tag[i]-=val;
        for(int i=l[belong[q[k].x]];i<q[k].x;i++) b[i]=b[i]-(val)+tag[belong[q[k].x]];
        for(int i=q[k].x+1;i<=r[belong[q[k].x]];i++) b[i]=b[i]-(val)+tag[belong[q[k].x]];
        tag[belong[q[k].x]]=0;
    }
    for(int i=belong[q[t].x]+1;i<=belong[m];i++) tag[i]-=val;
}
int main()
{
    cin>>n>>m;
    memset(minn,1,sizeof(minn));
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=m;i++) b[i]=a[i];
    block=sqrt(m);
    for(int i=1;i<=m;i++) belong[i]=(i-1)/block+1;
    for(int i=1;i<=m;i++) if(!l[belong[i]]) l[belong[i]]=i;
    for(int i=m;i>=1;i--) if(!r[belong[i]]) r[belong[i]]=i;
    for(int i=1;i<=belong[m];i++){
        for(int j=l[i];j<=r[i];j++) minn[i]=min(minn[i],b[j]);
    }
    for(int j=m+1;j<=n;){
        t=0;int val=find_dis();
        ans+=val;
        change(b[q[1].x]+tag[belong[q[1].x]]);
        for(int k=1;k<=t;k++){
            b[q[k].x]=a[j++];
            minn[belong[q[k].x]]=1e9;
            for(int i=l[belong[q[k].x]];i<=r[belong[q[k].x]];i++) minn[belong[q[k].x]]=min(minn[belong[q[k].x]],b[i]);
        }
    }
    ll kk=0;
    for(int i=1;i<=m;i++){
        kk=max(kk,b[i]+tag[belong[i]]);
    }
    printf("%lld\n",ans+kk);
}

5.莫队

更暴力的数据结构。

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+7;
int belong[MAXN],cnt[MAXN],aa[MAXN];
int n,m,size,block,now,ans[MAXN];
struct po{
    int l,r,id;
}q[MAXN];
int cmp(po a,po b){return (belong[a.l]^belong[b.l])?belong[a.l]<belong[b.l]:((belong[a.l]&1)?a.r<b.r:a.r>b.r);}
inline void add(int pos){
    if(!cnt[aa[pos]]) ++now;
    ++cnt[aa[pos]];
}
inline void del(int pos){
    --cnt[aa[pos]];
    if(!cnt[aa[pos]]) --now;
}
inline int read()
{
    int x=0,c=1;char ch=' ';
    while((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
    while(ch=='-') c*=-1,ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return x*c;
}
int main()
{
    n=read();
    size=sqrt(n);
    for(int i=1;i<=n;i++) belong[i]=(i-1)/size+1;
    for(int i=1;i<=n;i++) aa[i]=read();
    m=read();
    for(int i=1;i<=m;i++){
        q[i].l=read();q[i].r=read();q[i].id=i;
    }
    sort(q+1,q+m+1,cmp);
    int l=1,r=0;
    for(int i=1;i<=m;i++){
        int ql=q[i].l,qr=q[i].r;
        while(l<ql) del(l++);
        while(l>ql) add(--l);
        while(r<qr) add(++r);
        while(r>qr) del(r--);
        ans[q[i].id]=now;
    }
    for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
}