LDA算法理解

Blog MachineLearning

---

1 LDA（Latent Dirichlet Allocation）概述

隐含狄利克雷分布（Latent Dirichlet Allocation, LDA）算法由David Blei, Andrew Ng, Jordan Michaell于2003年提出，是一种主题模型。
作用是：将文档集中每篇文档的主题以概率分布的形式给出。
在获得了每篇文档上的隐含主题的概率分布后，我们就可以根据主题分布对文本进行处理（例如主题聚类和文本分类）。
其中一篇文档可以包含多个主题，文档中的每个词都由其中的某个主题生成。

1.1 基本术语解释

名词	含义
文档Document	非传统意义上的文档。LDA是词袋（bag of words）模型。将文档看作是是一组词，词与词之间没有先后顺序。
文档集（设共有M个文档）	训练集中所有文档的集合
词word	英文中即一个单词，中文中即独立意义的中文词
词表（设共有V个词）	文档集中所有出现过的词的集合（不重复）。
主题Topic	一个主题表现为该主题相关的一些词的集合，我们可以用V维的词表向量来表示主题k。向量的第i个元素表示的就是word i在该主题k下的概率，不出现在该主题k的词值就为0。向量的所有元素取值纸盒为1。
主题分布（设共有K个主题）	对于一篇文档而言，LDA认为其包含了多个主题。举例而言，对于某文档而言，主题1占20%的可能，主题2占50%的可能等等。主题分布即K个主题在文档上的分布

1.2 LDA的目的（一）

LDA的使用情景是：
对于一个文档集，我要在文档集中提取出K个主题来（K大小可以随意指定），
然后我想知道文档集中每篇文档在相对于这K个主题的主题分布，从而根据这些主题分布来对文档集中的文档进行一些处理（求解文本之间的相似度，对文本自动打标签）。

为了完成这个目标：
1. 我们首先得确定这K个主题都是啥（即这K个主题对应的V维词表向量分布）
2. 然后得确定这K个主题在每个文档上的主体分布（即M个文档对应的K维主题分布）

所以LDA的程序最终需要求解出的结果即为两个矩阵：

矩阵符号	维度	含义
$\theta$	$M*K$	代表的$M$篇文档，每篇文档上的主题分布。$\theta_i$代表的是第i篇文档上的主题向量。
$\phi$	$K*V$	代表$K$个主题，每个主题上的词频。$\phi_k$代表的是第k个主题上的词表向量

2 数学基础

LDA从生成模型的角度来看待文档和话题。

举例而言，通常人类写文章的步骤如下：

1. 选择一些与该文章相关的主题，例如军事和农业
2. 然后基于选定的主题遣词造句等等。

在LDA模型中，一篇文档生成的方式如下：

1. 从狄利克雷分布$\alpha$中取样生成文档$i$的主题分布$\theta_i$
2. 从狄利克雷分布$\beta$中取样生成主题$k$的词表分布$\phi_k$
3. 对于文档i中的每个单词位置来说，执行下列操作：
4. 从主题的多项式分布$\theta_i$ 中取样生成文档$i$的第$j$个词的主题$z_{i,j}$
5. 从词语的多项式分布$\phi_{z_i,j}$采样生成最终词语$w_{i,j}$

2.1 多项式分布Multinomial Distribuition

注意上面所描写的文档的生成方式中，暗示了无论是主题分布还是词表分布 其形式都是多项式分布。
多项式分布定义如下：

设$A_1,A_2,\dots,A_n$为某一试验的完备事件群，即事件$A_1,A_2,\dots,A_n$两两互斥，其和为完备事件群。
其中$A_1,A_2,\dots,A_n$的概率分别是$p_1,p_2,\dots,p_n$。
将该事件独立地重复N次，以$X_i$记为这N次试验中事件$A_i$出现的次数，则$X=(X_1,X_2,...,X_n)$是一个$n$维随机向量（$X_i$的取值范围为都是非负整数，且和为$N$）。
多维随机变量$X$的概率分布即为多项分布：

$$P(x_1,x_2,...,x_k;n,p_1,p_2,...,p_k)=\frac{n!}{x_1!...x_k!}p_1^{x_1}...p_k^{x_k}$$

我们来就多项式分布的定义分析下主体分布和词表分布：

多项式分布定义	主题分布$\theta_i$	词表分布$\phi_k$
基本事件	对于当前文档$i$的某个空白位置选择主题	对于当前文档的某个空白位置，在该空白位置主题已定的情况下，选择该空白位置填充词
基本事件的执行次数$N$	当前文档空白位置的个数	当前文档被分配给主题k的空白位置的个数
完备事件群$A_1,A_2,...,A_n$	$K$个主题构成完备事件群	$V$个词构成完备事件群
$p_1,p_2,\dots,p_n$	$\theta_{i1},\theta_{i2},...,\theta_{iK}$	$\phi_{i1},\phi_{i2},...,\phi_{iV}$
多维随机变量$X=(X_1,X_2,...,X_n)$	$X=(Topic_1, Topic_2 \dots Topic_K)$。$X_k$：当前文档$i$的空白位置中，分配给$Topic_k$的空白位置的个数	$X=(Word_1, Word_2 \dots Word_V)$。$X_j$：当前文档$i$的空白位置中，分配给$Topic_k$的空白位置中，$Word_j$的个数
$X \sim Multi(N;p_1,p_2,...,p_n)$	$X \sim Multi(L;\theta_{i1},\theta_{i2}\dots\theta_{iK})$（设当前文档有$L$个空白位置）	$X \sim Multi(L_k;\phi_{i1},\phi_{i2}\dots\phi_{iV})$（设当前文档被分配给主题$k$的空白位置的个数为$L_k$）

注意：对于LDA而言，我们最终所要求的两个矩阵，就是由主题分布和词表分布两个多项式分布的参数的参数构成。
所以，我们要求的就是多项式分布的参数。

2.2 Gamma函数

普通的阶乘仅适用于正整数域，而Gamma函数即为阶乘的一般形式，将阶乘拓展到正实数域。
Gamma函数形式：$\Gamma(x)=\int_0^{+\infty}e^{-t}t^{x-1}dt(x>0)$
Gamma函数具有如下性质：

• $\Gamma(x+1)=x\Gamma(x)$
• $\Gamma(n)=(n-1)!$

Gamma函数是定义在实数域上的阶乘运算，将阶乘这个操作从离散扩展到了连续。
任何用到离散阶乘的地方，都可以借助Gamma函数将概念从离散扩展到连续。

2.3 二项分布与Beta分布

2.3.1 二项分布

二项分布即是重复了$n$次的伯努利分布，其概率密度函数为$P(K=k)=\binom{n}{k}p^k(1-p)^{n-k}$
注意：二项式分布是离散概率分布，并且其中也出现了阶乘。

2.3.2 Beta分布

Beta分布$X \sim Beta(\alpha, \beta)$，指的是定义在区间$(0,1)$上的连续概率分布，他有两个参数$\alpha$和$\beta$。
其概率密度函数如下所示：

$$f(x;\alpha,\beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_0^1u^{\alpha-1}(1-u)^{\beta-1}du}$$
对于上式而言，我们观察可以得出，分母部分是一个归一化参数。因为对于连续概率分布而言，其概率密度函数必然要保证在定义域内的基本为1（否则不能称之为概率密度函数）。

因此，我们可以假设Beta分布其实是我们为了某个目的认为构造出来的概率分布（仅为了帮助理解）：
我们先构造了Beta分布概率密度函数的一部分，即分子$x^{\alpha-1}(1-x)^{\beta-1}$。然后为了使得概率密度函数积分为1，给概率密度函数添加了一个分母$B(a,b)=\int_0^1\mu^{\alpha-1}(1-\mu)^{\beta-1}d\mu$。

上面公式通常会写作以下形式，即将分母部分利用$B(\alpha,\beta)$来显示：

$$f(x;\alpha,\beta)=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{\int_0^1u^{\alpha-1}(1-u)^{\beta-1}du} \\ =\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}$$
注意，我们可以证明$B(\alpha,\beta)=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$[1]。

对比一下二项式分布和Beta分布，我们可以发现他们的概率密度函数在剔除掉系数之后很相似。而且二项式分布的系数是$\binom{n}{k}$，带有阶乘；Beta分布的系数是$\frac{1}{B(\alpha,\beta)}=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}$，带有Gamma函数。
因此，这其实就相当于二项式分布借由Gamma函数从离散扩充到了连续。

2.3.3 Beta分布的期望

如果$p \sim Beta(t|\alpha,\beta)$，则

$$E(p)=\int_0^1t \cdot Beta(t|\alpha, \beta)dt \\ =\int_0^1t\cdot \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}t^{\alpha-1}(1-t)^{\beta-1}dt \\ = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\int_0^1 t^{\alpha}(1-t)^{\beta-1}dt$$
对于式子$\int_0^1 t^{\alpha}(1-t)^{\beta-1}dt$而言，我们联想到$Beta(t|\alpha+1,\beta)$的概率密度函数为 $$f(x;\alpha,\beta)=\frac{\Gamma(\alpha+\beta+1)}{\Gamma(\alpha+1)\Gamma(\beta)}t^\alpha(1-t)^{\beta-1}$$ ，则因为概率密度函数积分为1，所以
$$\int_0^1\frac{\Gamma(\alpha+\beta+1)}{\Gamma(\alpha+1)\Gamma(\beta)}t^\alpha(1-t)^{\beta-1}dt=1$$
将上式带回到$E(p)$中，并根据$Gamma$函数的性质可得
$$E(p)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\cdot\frac{\Gamma(\alpha+1)\Gamma(\beta)}{\Gamma(\alpha+\beta+1)}=\frac{\alpha}{\alpha+\beta}$$
因此，Beta分布的均值就可以用$\frac{\alpha}{\alpha+\beta}$来估计。

2.3.4 多项式分布与狄利克雷分布

对比一下上述所提到的四个分布，如下表所示

分布名称	概率密度函数	参数
二项分布	$P(K=k)=\binom{n}{k}p^k(1-p)^{n-k}$	参数为$p$和$1-p$，参数约束为：$p+(1-p)=1$
多项分布	$$P(x_1,x_2,...,x_k;n,p_1,p_2,...,p_k)=\frac{n!}{x_1!...x_k!}p_1^{x_1}...p_k^{x_k}$$	参数为$p_1,p_2\dots p_n$，参数约束为：$p_1+p_2+\dots+p_n=1$
$Beta$分布	$$f(x;\alpha,\beta)=\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}$$ ，其中 $$\frac{1}{B(\alpha,\beta)}=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}$$	参数为$\alpha$和$\beta$
$Dirichlet$分布	$$f(x_1,x_2\cdots x_k;\alpha_1,\alpha_2\cdots \alpha_k)=\frac{1}{B(\alpha)}\prod_{i=1}^kx_i^{\alpha^i-1}$$ 其中， $$B(\alpha)=\frac{\prod_{i=1}^k\Gamma(\alpha^i)}{\Gamma(\sum_{i=1}^k\alpha^i)}$$	参数为$\alpha_1,\alpha_2\dots \alpha_k$

由上述表格内容可以看出：

• 多项分布是二项分布在多维变量上的推广
• $Dirichlet$分布式$Beta$分布在多维变量上的推广　

2.3.5 Dirichlet分布的期望

参见Beta分布的期望，因为$Dirichlet$分布是Beta分布在多维变量的推广，所以我们可以得出如下结论（证明参考Beta分布的期望证明，略）：

$$E(\vec{p})=(\frac{\alpha_1}{\sum_{i=1}^K\alpha_i},\frac{\alpha_2}{\sum_{i=1}^K\alpha_i} \dots \frac{\alpha_K}{\sum_{i=1}^K\alpha_i})$$

2.4 共轭先验分布

2.4.1 贝叶斯定理

$$p(\theta|x)=\frac{p(x|\theta)p(\theta)}{p(x)}=\frac{p(x|\theta)p(\theta)}{\int p(x|\theta)p(\theta)d\theta}\propto p(x|\theta)p(\theta)$$
这个公式中：$\theta$表示参数，$x$是已观测到的数据。

• $p(\theta|x)$：后验概率，在已经观测到了数据$x$的情况下，参数为$\theta$的概率。
• $p(\theta)$：先验概率，在没有观测到数据x的情况下，参数为$\theta$的概率。
• $p(x|\theta)$：似然函数，参数为$\theta$的情况下，产生观测数据为$x$的概率。
• $P(x)$：归一化常数，通常不会直接求，而是忽略掉，最后利用归一化（概率密度函数积分必须为1）来处理，例如上式中所示。

由贝叶斯定理可知，后验分布$\propto$似然函数*先验分布。

而共轭先验分布的定义如下：
如果先验分布和似然函数可以使得先验分布和后验分布具有相同的形式，则称先验分布是似然函数的共轭先验分布

2.4.2 Beta分布是二项式分布的共轭先验分布

因为多项式分布和$Dirichlet$分布式二项式分布和$Beta$分布的多维推广，所以我们在此只证明$Beta$分布式二项分布的共轭先验分布。

要证明$Beta$分布式二项分布的共轭先验分布，则根据共轭先验分布的定义，似然函数是二项分布的形式，先验分布是$Beta$分布的形式，我们想要让后验分布也是$Beta$分布的形式。
证明：
1. 似然函数$p(x|\theta)$是二项分布，$\theta$即为二项分布的参数$p$，似然函数即为

$$L=\binom{s+f}{s}p^s(1-p)^f$$ 其中$s$表示$n$次试验中成功的次数，$f$表示$n$次试验中失败的次数，$n=s+f$。
2. 先验分布$p(\theta)$是$Beta$分布，即$\theta$是$beta$分布以$\alpha$和$\beta$为参数的结果，先验分布即为 $$P(p|\alpha,\beta)=\frac{p^{\alpha-1}(1-p)^{\beta-1}}{B(\alpha,\beta)}$$ 其中$B(\alpha,\beta)=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}$
3. 根据后验分布$\propto$似然函数*先验分布可得： $$P(p|s,f,\alpha,\beta)=\frac{\binom{s+f}{s}p^s(1-p)^f\frac{p^{\alpha-1}(1-p)^{\beta-1}}{B(\alpha,\beta)}}{\int_{q=0}^1\binom{s+f}{s}p^s(1-p)^f\frac{p^{\alpha-1}(1-p)^{\beta-1}}{B(\alpha,\beta)}dq} \\ = \frac{p^{s+\alpha-1}(1-p)^{f+\beta-1}}{\int_{q=0}^1p^{s+\alpha-1}(1-p)^{f+\beta-1}dq} \\ = \frac{p^{s+\alpha-1}(1-p)^{f+\beta-1}}{B(s+\alpha,f+\beta)}$$

因此，我们会发现后验分布也是Beta分布。
而且先验分布是$X\sim Beta(\alpha,\beta)$，后验分布则是$X\sim Beta(\alpha+s, \beta+f)$。
超参数$\alpha$和$\beta$在基于观测到的数据$s$和$f$后发生了改变，变成了$\alpha+s$和$\beta+f$，但形式上仍然是$Beta$分布。
如果以后再有新的数据的话，我们仍然可以在了$\alpha+s$和$\beta+f$的基础上继续更新超参数。

2.4.3 Dirichlet分布是多项式分布的共轭先验分布

先验分布是$Dir(\vec{p}|\vec{a})$，后验分布就变成了$Dir(\vec{p}|\vec{\alpha}+\vec{x})$。
注意：

• $\vec{p}$：多项式分布的参数，同时也是$Dirichlet$分布的结果/随机变量。
• $\vec{\alpha}$：$Dirichlet$分布的参数。
• $\vec{x}$：观测到的数据。第$i$维代表事件$i$发生的次数（如果将$Beta$分布看做是二维的$Dirichlet$分布的话，那么$x_1=s,x_2=f$）。
  $\vec{p},\vec{\alpha},\vec{x}$这三个向量维度相同。

2.5 LDA的目的（二）

我们在LDA的目的（一）中提到，LDA目的最终要求出的是两个矩$\theta$和$\phi$，这两个矩阵又都是多项式分布的参数。而根据共轭先验分布，多项式分布的参数即为$Dirichlet$分布的结果/随机变量，因此我们可以用$Dirichlet$分布随机变量的期望来估计多项式分布的参数。
结合上面所提到的，$Dirichlet$分布的期望公式如下：

$$E(\vec{p})=(\frac{\alpha_1}{\sum_{i=1}^K\alpha_i},\frac{\alpha_2}{\sum_{i=1}^K\alpha_i} \dots \frac{\alpha_K}{\sum_{i=1}^K\alpha_i})$$
根据共轭先验分布的结论，$Dirichlet$分布的参数有最开始的$\vec{\alpha}$变成了$\vec{\alpha}+\vec{x}$，其中$\vec{\alpha}$是我们预先设定好的参数，$\vec{x}$则是训练数据中隶属于每个主题词的个数（如果将$Beta$分布看做是二维的$Dirichlet$分布的话，$\vec{x}$为二维，值分别是$x_1=s,x_2=f$）。因此我们只需要识别出对于文档中的每个词来说，该词属于哪个隐含主题，然后就可以按照上述公式来计算出来两个矩阵。

因此，我们所要求解的就是$p(\vec{z}|\vec{w})$，即文档集中的每个词背后所隐含的主题。

注意：$\vec{w}$是文档集中的词向量，$\vec{z}$是文档集中与词向量所对应的每个主题值。
举例而言，如果对于文档集，只有一个文档，该文档分词后有5个词，"aaa bbb ccc ddd aaa"。
然后我们要从文档集中提取出来3个主题$topic0,topic1,topic2$。
词"aaa"被赋予的隐含主题为$topic0$，词"bbb"被赋予的隐含主题为$topic2$，词"ccc"被赋予的隐含主题维$topic0$，词"ddd"被赋予的隐含主题为$topic1$。
则$\vec{w}=(aaa,bbb,ccc,ddd,aaa), \vec{z}=(topic0，topic2,topic0,topic1,topic0)$。
$\vec{w}$和$\vec{z}$的维度都是整个文档集中词的个数（重复词不合并）。

根据条件概率公式

$$p(\vec{z}|\vec{w})=\frac{p(\vec{w},\vec{z})}{p(\vec{w})}$$
但是对于该公式而言，对其分母利用离散概率分布求解边缘概率的方法进行展开。
$$p(\vec{w})=\sum_zp(\vec{w},\vec{z})=\prod_{i=1}^n\sum_{k=1}^Kp(w_i|z_i=k)p(z_i=k)$$
其中$n$是文档集中所有词的个数，也即为$\vec{w}$和$\vec{z}$的维度（对于前面所举出的文档集的例子，$n=5$），$K$是索要提取出的隐含主题的个数（前面例子中$K=3$）。
因此对于分母而言，其计算量高达$K^n$，难以计算。
所以我们采用Gibbs Sampling的方法来计算。

3 Gibbs Sampling吉布斯采样

吉布斯采样是马尔科夫链蒙特卡罗法（Markov Chain Monte Carlo, MCMC）的一种。

3.1 Monte Carlo蒙特卡罗法

蒙特卡罗法即通过模拟采样的方式来让你获得想要的值。
举个例子，在一个正方形内，以正方形的中心为原点，边长为直径画一个圆（即正方形的内切圆）。
向正方形内均匀撒米，那么按道理来说圆内的米粒C与正方形内的米粒S满足：$\frac{C}{S} \approx \frac{\pi(\frac{d}{2})^2}{d^2}$
因此对于参数$\pi$来说，我们可以用$\pi\approx \frac{4C}{S}$来对它进行估计。

3.2 Markov Chain马尔科夫链

马尔科夫链即根据转移矩阵去转移的随机过程（马尔科夫过程）。
如下图就是一个典型的马尔科夫过程

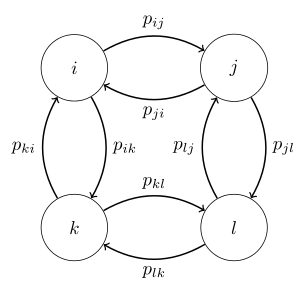
该状态转移图的转移矩阵如下图所示：

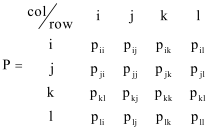
其中，$i,j,k,l$表示的马尔科夫链上的状态。$pij$表示从状态$i$到状态$j$转移的可能性。
现在利用向量$\pi=(i,j,k,l)$表示当前所处的状态。开始的时候$\pi_0=(1,0,0,0)$表示最开始处于状态$i$。
那么下一次转移后$\pi$变为$\pi_1=\pi_0*P=[P_{ii},P_{ij},P_{ik},P_{il}]$，此处向量$\pi_1$其实就是第一次转移之后的状态分布，即有$P_{ii}$的概率身处状态$i$，有$P_{ij}$的概率身处状态$j$。

3.2.1 平稳状态分布Stationary Distribution

有一种情况，即向量$\pi$在经过大量的转移后达到一个稳定状态，之后即使再怎么转移$\pi$的值也不会改变了。此时$\pi$即成为平稳状态分布。（如果在平稳状态下我们继续在马尔科夫链中转移$n$次，那么即$n$次转移中位于状态$i$的次数为$\pi*P$）。
要达到这个平稳状态分布需要满足一些条件，即$\pi P=\pi$(也即$\pi_iP_{ij}=\pi_jP_{ji}$，这两个条件等价)。
举例而言，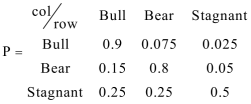
如果初始状态$\pi=(1,0,0)$的话，在多次乘以转移矩阵$p$之后，$\pi$最终等于$(0.625,0.3125,0.0625)$。这也就意味着如果我们在$\pi$收敛后继续转移状态的话，我们10000次转移，大约有6250次位于Bull状态，3125次位于Bear状态，625词位于Stagnant状态。
其实$\pi$就是一个概率分布，而我们构造出某个马尔科夫链（即转移矩阵）使得收敛到平稳状态分布后采样出来的结果满足$\pi$这个概率分布。
因此如果我们想求某个概率分布$P(X)$的话，我们就可以构造一个马尔科夫链来使得最终平稳状态分布就是概率分布$P(X)$，从而在无需明显求出$P(X)$表达式的情况下获取其采样结果。

3.3 Metropolis-Hasting算法

MH算法目的：根据一个需求的概率分布$P(x)$生成（采样）一系列的样本状态点。
为达到这一目的，MH算法通过构造马尔科夫链来使得该马尔科夫链最终的平稳分布为$P(X)$，然后再进行采样即可。
对于平稳状态分布的条件而言：

$$P(x)p(x->x')=P(x')p(x'->x)$$
$$\frac{p(x->x')}{p(x'->x)} = \frac{P(x')}{P(x)}$$
将转移概率$p(x->x')$分解为建议概率$g(x->x')$和接受概率$A(x->x')$，即$p(x->x')=g(x->x')A(x->x')$。建议概率是我们给出状态$x$后转移到状态$x'$的条件概率，而接受概率则是接受状态$x'$的条件概率。
则整理可得，
$$\alpha=\frac{A(x->x')}{A(x'->x)}=\frac{P(x')}{P(x)}\frac{g(x'->x)}{g(x->x')}$$
这样我们得到了接受率$\alpha$，代表的含义是：从状态$x$到状态$x'$的接受概率与从状态$x'$到状态$x$的接受概率的比率。对于$\alpha$来说，如果它大于1，就寿命下次要转移的状态X'比当前状态Xi可能性更大，那么我们就按照建议概率$g(x->x')$所建议的，转移到$x'$。如果它不大于1，例如为0.7，那么我们就有0.7的概率接受建议概率的建议转移到$x'$，有0.3的概率拒绝建议概率的建议仍然留在$x$处。
所以最终的话，我们倾向于留在高概率密度的地方，然后仅偶尔跑到低概率状态的地方（这也就是MH算法直观上的运行机理）。
MH算法将接受率$\alpha$添加了个上界1，得到如下的公式：
$$\alpha=A(x->x')=min\{1, \frac{g(x'->x)}{g(x->x')}\}$$
因此，MH算法的步骤为：
1. 选择任意一个状态点$Xt$作为初始状态。
2. 选择任意一个概率分布作为建议概率$g(x|y)$（建议概率是条件概率，而且必须满足$g(x|y)=g(y|x)$。通常会选择以$y$点为中心的正态分布）
3. 根据$g(X'|Xt)$生成下次状态点$X'$，计算接受率$\alpha$
4. 如果$\alpha==1$，则说明$X'$比$Xt$更有可能，因此就接受这次转移，下次状态点的状态就是X'
5. 如果$\alpha<1$，则以$\alpha$的概率接受这次转移。
6. 继续循环3-5步即可。

3.4 Gibbs Sampling算法

MH默认的流程是任意选择转移概率$g(x)$，然后利用接受率$\alpha$来使得采样最终收敛于$p(x)$。但是如果我选择足够好的$g(x)$，使得$g(x)$每次发出的建议都是符合$P(x)$分布的建议，那么我就一直接受就行了(此时即接受率恒为1)。Gibbs Sampling采用的就是这种方式。

对于多维随机变量的概率分布$p(\vec{x})$而言，选择完全条件概率full conditionals 作为建议概率，

$$p(x_j|x_{-j})=p(x_j|x_1,\dots,x_{j-1},x_{j+1},\dots,x_n)=\frac{p(x_1,\dots,x_n)}{p(x_1,\dots ,x_{j-1},x_{j+1},\dots,x_n)}$$
此时可以证明的是接受率$\alpha$恒等于1，即$g(x)$每次发出建议都是符合联合概率分布的，因此我们只需要一直接受建议即可。
证明如下：

所以，对于多维随机变量的概率分布而言，一旦其完全条件概率full conditionals 可用，则可以采用$n$维向量轮流每个维度循环的方式来迭代达到平衡。

3.5 LDA模型的Gibbs Sampling应用

由2.5节可知，LDA模型所要计算的是$p(\vec{z}|\vec{w})$。
其中$\vec{w}$是文档集中的单词，是已知的可观测变量，所以我们把它当做已知值，则LDA想要的概率分布就是$p(\vec{z})$。而又因为$\vec{z}$是多维随机变量，结合前面Gibbs Sampling的思想，所以我们选取其完全条件概率$p(z_i|\vec{z}_{-i})$作为马尔科夫链的转移概率。此时考虑$\vec{w}$的因素，所以我们要用$p(z_i|\vec{z}_{-i},\vec{w})$作为转移概率。

3.5.1 整个文本训练集生成的联合概率

要得到完全条件概率$p(z_i|\vec{z}_{-i},\vec{w})$，我们必须得到整个文本集生成的联合概率分布$p(\vec{w},\vec{z})$。

$$p(\vec{w},\vec{z})=p(\vec{w}|\vec{z})p(\vec{z}))$$
即 $$p(\vec{w},\vec{z}|\vec{\alpha},\vec{\beta})=p(\vec{w}|\vec{z},\vec{\beta})p(\vec{z}|\vec{\alpha})$$
我们将两个因子分开处理。

对于第一项因子$p(\vec{w}|\vec{z},\vec{\beta})$来说，先考虑$p(\vec{w}|\vec{z},\phi)$（先不考虑$\beta$的因素，将$\phi$看做常数），则

$$p(\vec{w}|\vec{z},\phi)=\prod_{i=1}^Wp(w_i|z_i)=\prod_{i=1}^w\phi_{z_i,w_i}$$
注意$W$是文档集中的所有词的个数（并非词表中的词个数$V$），$\vec{w}$是文档集中的词向量，$\vec{z}$是文档集中与词向量所对应的每个主题值。

我们将这一项分解成两个连乘，一个相对于词表，一个相对于topic。
首先，对于topic确定的情况下，$p(\vec{w}|z_i=k,\phi)=\prod_{t=1}^V \phi_{k,t}^{n_k^t}$。$n_k^t$表示的是整个文档集中隶属于topic k的词t的个数。
又因为同一个词可能被不同的topic生成（只是生成的概率不同而已，例如topic "农业"生成词"小麦"的概率可能为0.5，但topic“军事”生成词"小麦"的概率就可能只是0.01），那么我们在添上对于topic的连乘，即$p(\vec{w}|\vec{z},\phi)=\prod_{k=1}^K \prod_{t=1}^V \phi_{k,t}^{n_k^t}$

所以

$$p(\vec{w}|\vec{z},\vec{\beta})=\int p(\vec{w}|\vec{z},\phi) p(\phi|\vec{\beta}) d\phi$$
而$p(\phi_k|\vec{\beta})=Dir(\phi_k|\vec{\beta})=\frac{1}{B(\alpha)}\prod_{t=1}^V \phi_{k,t}^{\beta_t-1}$
所以$p(\phi|\vec{\beta})=\prod_{k=1}^K Dir(\phi_k|\vec{\beta})=\prod_{k=1}^K \frac{1}{B(\alpha)}\prod_{t=1}^V \phi_{k,t}^{\beta_t-1}$
所以 $$p(\vec{w}|\vec{z},\vec{\beta})=\int p(\vec{w}|\vec{z},\phi) \cdot p(\phi|\vec{\beta}) d\phi \\ = \int \prod_{k=1}^K \prod_{t=1}^V \phi_{k,t}^{n_k^t} \cdot \prod_{k=1}^K \frac{1}{B(\vec{\beta})}\prod_{t=1}^V \phi_{k,t}^{\beta_t-1} d\phi \\ = \prod_{k=1}^K \frac{1}{B(\vec{\beta})} \int \prod_{t=1}^V \phi_{k,t}^{n_k^t+\beta_t-1} d\phi \\ = \prod_{k=1}^K \frac{B(\vec{n_k}+\vec{\beta})}{B(\vec{\beta})}$$
其中$\vec{n_k}=(n_k^0,n_k^1 \dots n_k^V)$。

对于因子2来说，同理可得：

$$p(\vec{z}|\theta) = \prod_{i=1}^W p(z_i|d_i)=\prod_{m=1}^M \prod_{k=1}^K p(z_i=k|d_i=m)=\prod_{m=1}^M \prod_{k=1}^K \theta_{m,k}^{n_m^k}$$ 。$n_m^k$表示的是第m个文档中属于第k个主题的词的个数。
同样积分可得：
$$p(\vec{z}|\vec{\alpha})=\int p(\vec{z}|\theta)p(\theta|\vec{\alpha}) d\theta \\ =\prod_{m=1}^M \frac{1}{B(\vec{\alpha})} \int \prod_{k=1}^K \theta_{m,k}^{n_m^k+\alpha_k-1} d\vec{\theta_m} \\ = \prod_{m=1}^M \frac{B(\vec{n_m}+\vec{\alpha})}{B(\vec{\alpha})}$$
其中$\vec{n_m}=(n_m^1,n_m^2\dots n_m^K)$

所以，文档集中生成的联合分布为

$$p(\vec{w},\vec{z}|\vec{\alpha},\vec{\beta})=p(\vec{w}|\vec{z},\vec{\beta})p(\vec{z}|\vec{\alpha}) \\ = \prod_{k=1}^K \frac{B(\vec{n_k}+\vec{\beta})}{B(\vec{\beta})} \cdot \prod_{m=1}^M \frac{B(\vec{n_m}+\vec{\alpha})}{B(\vec{\alpha})}$$

3.5.2 Collapsed Gibbs Sampling公式

为清晰起见我们更改下联合分布式子的符号表示，将$B(x)$改为$\Delta(x)$。则

$$p(\vec{w},\vec{z}|\vec{\alpha},\vec{\beta})=p(\vec{w}|\vec{z},\vec{\beta})p(\vec{z}|\vec{\alpha}) \\ = \prod_{k=1}^K \frac{\Delta(\vec{n_k}+\vec{\beta})}{\Delta(\vec{\beta})} \cdot \prod_{m=1}^M \frac{\Delta(\vec{n_m}+\vec{\alpha})}{\Delta(\vec{\alpha})}$$

其中：

• $\vec{n_k}=(n_k^0,n_k^1 \dots n_k^V)$，$n_k^t$表示的是整个文档集中隶属于topic k的词t的个数。
• $\vec{n_m}=(n_m^1,n_m^2\dots n_m^K)$，$n_m^k$表示的是第m个文档中属于第k个主题的词的个数。
• $\Delta(\vec{\alpha})=\frac{\prod_{k=1}^K \Gamma(\alpha_k)}{\Gamma(\sum_{k=1}^K \alpha_k)}$

我们所要求的完全条件概率如下：

$$p(z_x=k|\vec{z_{-x}},\vec{w})=\frac{p(\vec{w},\vec{z})}{p(\vec{w},\vec{z_{-x}})}$$
注意，对于这个公式而言，

• 因为当前仅处理文档集中的第$x$个单词$W_x$（若该单词位于第$m$篇文档，且其隐含主题为第$k$个主题，该单词是词表中的第$i$个词），因此与$topic_k$和$doc_m$无关的均被视为常数忽略，因此消去了$\prod$符号。
• 而分母的$\Delta(\vec{\beta}),\Delta(\vec{\alpha})$也由于分子分母都有而消去了。

则因此

$$p(z_x=k|\vec{z_{-x}},\vec{w})=\frac{p(\vec{w},\vec{z})}{p(\vec{w},\vec{z_{-x}})} \\ \propto \frac{\Delta(\vec{n_k}+\vec{\beta})}{\Delta(\vec{n_{k,-i}}+\vec{\beta})} \cdot \frac{\Delta(\vec{n_m}+\vec{\alpha})}{\Delta(\vec{n_{m,-i}}+\vec{\alpha})}$$

首先我们来看第一个因子的分母部分，

$$\Delta(\vec{n_{k,-i}}+\vec{\beta})=\frac{\prod_{t=1}^V \Gamma(n_{t,-i}+\beta_t)}{\Gamma(\sum_{t=1}^V n_{t,-i}+\beta_t)} \\ = \frac{\Gamma(n_1+\beta_1)\Gamma(n_2+\beta_2) \dots \Gamma(n_i-1+\beta_i) \dots \Gamma(n_V+\beta_V)}{\Gamma(\sum_{t=1}^V n_{t,-i}+\beta_t)} \\ \text{(只有第i个单词需要减1，即减去当前单词的影响)}$$
上面公式中，V为字典中词的个数。

同理，分子部分的话，

$$\Delta(\vec{n_k}+\vec{\beta})=\frac{\prod_{t=1}^V \Gamma(n_t+\beta_t)}{\Gamma(\sum_{t=1}^V n_t+\beta_t)} \\ = \frac{\Gamma(n_1+\beta_1)\Gamma(n_2+\beta_2) \dots \Gamma(n_i+\beta_i) \dots \Gamma(n_V+\beta_V)}{\Gamma(\sum_{t=1}^V n_t+\beta_t)}$$

因此，第一个因子即如下：

$$\frac{\Delta(\vec{n_k}+\vec{\beta})}{\Delta(\vec{n_{k,-i}}+\vec{\beta})} = \frac{\Gamma(n_i+\beta_i)}{\Gamma(n_i-1+\beta_i)} \cdot \frac{\Gamma(\sum_{t=1}^V n_{t,-i}+\beta_t)}{\Gamma(\sum_{t=1}^V n_t+\beta_t)} \\ (基于\Gamma(x+1)=x\Gamma(x)) \\ = (n_i-1+\beta_i) \cdot \frac{1}{\sum_{t=1}^V (n_{t,-i}+\beta_t)} = \frac{n_i-1+\beta_i}{\sum_{t=1}^V (n_{t,-i}+\beta_t)}$$

同理，第二个因子为：

$$\frac{\Delta(\vec{n_m}+\vec{\alpha})}{\Delta(\vec{n_{m,-i}}+\vec{\alpha})} = \frac{\Gamma(n_k+\alpha_k)}{\Gamma(n_k-1+\alpha_k)} \cdot \frac{\Gamma(\sum_{t=1}^K n_{t,-i}+\alpha_t)}{\Gamma(\sum_{t=1}^K n_t+\alpha_t)} \\ (k是z_i=k的那个k号主题) \\ = \frac{n_k-1+\alpha_i}{\sum_{t=1}^K (n_{t,-i}+\alpha_t)}$$

所以，最终我们得到了如下结果：

$$p(z_i=k|\vec{z_{-i}},\vec{w})=\frac{p(\vec{w},\vec{z})}{p(\vec{w},\vec{z_{-i}})} \\ = \frac{n_i-1+\beta_i}{\sum_{t=1}^V (n_{t,-i}+\beta_t)} \cdot \frac{n_k-1+\alpha_i}{\sum_{t=1}^K (n_{t,-i}+\alpha_t)} \\ (通常我们把超参数\vec{\alpha}和\vec{\beta}的每个元素值设为相同值，即对称超参数) \\ = \frac{n_{k,-i}^{(t)}+\beta}{\sum_{t=1}^V n_{k,-i}^{(t)}+V\beta)} \cdot \frac{n_{m,-i}^{(t)}+\alpha}{\sum_{t=1}^K (n_{m,-i}^{(t)}+K\alpha)}$$

其中，

• $n_{k,-i}^{(t)}$即$n_i-1$，表示第k个topic的第i个单词个数-1
• $n_{m,-i}^{(t)}$即$n_k-1$，表示第m个文档的第k个主题词数-1

3.5.3 计算隐含主题的概率分布

上一节中我们已经的出来采样公式，所以在多次循环采样后，我们就能得到文档集中的每个词的主题赋值。
然后根据2.5节LDA的目的（二）所说，知道了每个词的主题，我们利用Dirichlet分布的期望公式，就可以得到隐含主题的两个概率分布矩阵$\phi$和$\theta$了。

$$\theta_{mat}=[\vec{\theta_1}, \vec{\theta_2} \dots \vec{\theta_M}]$$
则第m篇文章的第k个主题：
$$\theta_{m,k} = \frac{n_{m,k}+\alpha_k}{\sum_{i=1}^K (n_{m,i}+\alpha_i)} \\ (引入对称超参数) \\ = \frac{n_{m,k}+\alpha}{\sum_{i=1}^K n_{m,i}+K\alpha)}$$

同理，

$$\phi_{mat}=[\vec{\phi_1}, \vec{\phi_2} \dots \vec{\phi_K}]$$
第k个主题的第w个词：
$$\phi_{m,k} = \frac{n_{k,w}+\beta_w}{\sum_{i=1}^V (n_{k,i}+\beta_i)} \\ (引入对称超参数) \\ = \frac{n_{k,w}+\beta}{\sum_{i=1}^V n_{k,i}+V\beta)}$$

到此为止，LDA算法的所要达到的目的我们已经获取到了，LDA算法的大致流程也已经都写了下来。另外，LDA的计算方法除了Gibbs Sampling之外还有一种方法是变分贝叶斯，大家有兴趣可以去了解一下思想。

4 参考资料

• LDA漫游指南-马晨
• Gibbs Sampling for the Uninitiated
• 通俗理解LDA主题模型
• 机器学习-周志华
• Metropolis-Hasting algorithm-Wikipedia
• Introduction to Stationary Distribution
• Probabilistic Topic Models