美丽的根

翻译

---

原文地址

John Baez 2011.12.15

在2016年，我的朋友Dan christensen做出了一个奇妙的图片，勾画了小于5阶，且整数系数范围在-4到4之间的所有多项式的所有根。

点击此图片放大观察。二阶多项式的根是灰色的。三阶多项式是蓝绿色的。五阶多项式是黑色的。对称的横轴是实轴，对称是竖轴是虚轴。在中间的0处产生最大空洞，第二大的洞在±1处，并且在±i处和1的第六个根处也有洞。

你可以在这个图中看到很多这样奇特的图案，比如整数系数的多项式的根试图在避开整数和单位根-除了他们落在了这些点的右边！如果你放大，可以看到更多这样的图案。

现在你可以看到在实轴点1处那些围绕空白区域的美丽的羽毛，一个围绕在exp(iπ/3)的的六边形星星，一条从这一点到点1的奇怪的红色曲线，围绕其他点的小星星，等等...

人们应该学习这些！我们来定义Christensen 集合$C_{d,n}$ 来作为所有d阶多项式的所有根，其整数系数的范围从-n到n。显然$C_{d,n}$ 的范围会随着d或n变大而增大，并且在复平面n趋于无穷，d≥1的情况下变的更密集。如果固定d≥1且$n\to\infty$，我们会得到所有的有理复数。如果让$d,n\to\infty$，我们会得到所有的代数复数。基于上面的图片，如果让n固定，$d\to\infty$，会得到很多有趣的猜想。

由上图的启发，Sam Derbyshire 决定做一些多项式根的高分辨率的图像。通过一些实验，他决定从系数范围-1到1（不包括0）的多项式入手。他计算了小于24阶的所有多项式的所有根，并制作了一个高清图像。有$2^{24}$个的多项式，大概有$24×2^{24}$个根—大概4亿个根！这个花费Mathematica大概4天的时间来生成根的坐标，生成了大概5G的数据。之后他利用java来生成这个惊艳的图片：

颜色表示了根的密集程度，从黑色到深红色，再到黄色，再到白色。上图是一个90M数据文件的低分辨率版本，我们可以放大看一下更多的细节：

注意那些在单位根的空洞，以及我们在单位圆内看到的像羽毛一样的图案。我们放大这部分区域来观察,区域标记如下：

这是在1处的空洞的特写：

注意沿着实轴的白线。这是因为有实根的多项式比接近实根的多项式多很多。

接下来我们看i的空洞：

以及在$exp(iπ/4) = (1+i)/\sqrt2$ :

注意越接近这个点，根的密集程度越大，但是突然在右侧减少。注意根密度的微妙图案。

不过，羽毛结构越靠近单位圆内部越美丽!下图是他们在实轴附近的图案，此图案是在点4/５处生成的：

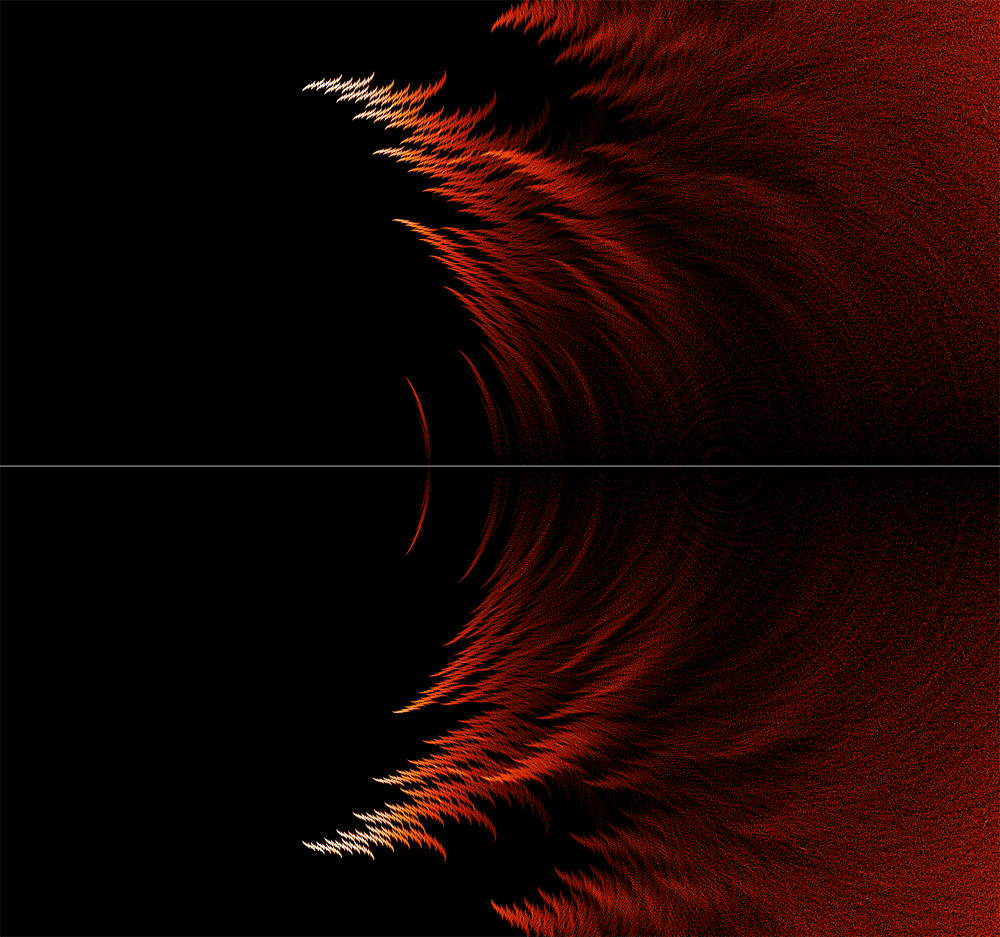
在靠近点$(4/5)i$处有不同的特性：

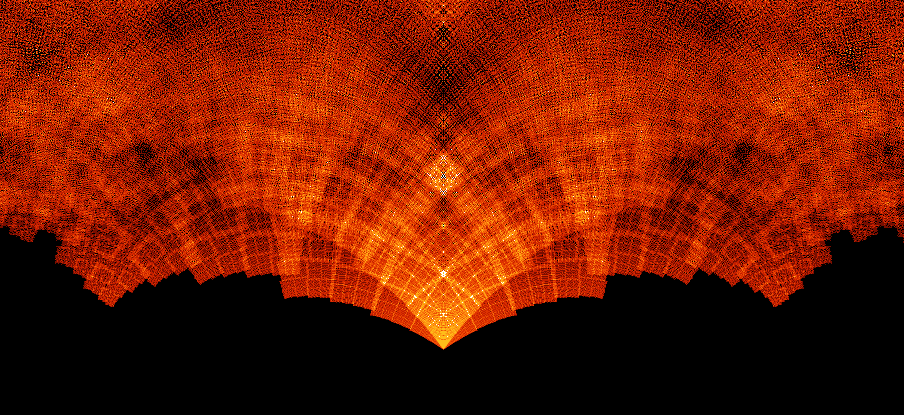
但是我认为最漂亮的是在点$(1/2)exp(i/5)$附近。这个图像几乎是现在的一个隐喻，在我们的数学学习中，图案从混沌中浮现就像从薄雾中隐现明确的数字。

你会沉醉与我刚展示的图案，而且一开始会有些许神秘色彩。Jesse C. McKeown 和 Greg Egan在“week285”的讨论中搞明白了如何理解它们。故事的结果是非常美妙的。但是这个讨论有点难理解，因为是聪明的人按照自己的思路来解释的。所以，我怀疑人们是否能理解它--至少有一部分人能理解。让我们先尝试解释一个图案，为什么接近$\frac12e^{i/5}$的区域是这样的：

看这个多像一个龙形

你可以利用各种方法创建一个龙形图案。在上面的动图里，我们从一条水平直线开始（这样不会显得愚蠢），之后一直在重复做相同的事情。也就是，在每一步我们用两个短线段在直角处替换之前的线段。

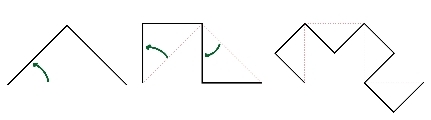
在每一步，我们有一个连续的曲线。龙在无穷多步骤之后也是一个连续的曲线。但是它是空间充填率曲线，是非零区域！

另一种更合理的生成龙形图案的方法，在复平面中采用下面两个公式：

$$f_+(x) = \frac{1+i}2x$$
$$f_-(x) = 1-\frac{1-i}2x$$

在复平面选取一个点，持续随机使用这两个函数中的任意一个。无论你选择哪个，你会得到收敛的序列，并且收敛与一个龙形图案！我们可以利用这种方法得到龙形图案的所有点。

但是这两个方程是从哪里来的？它们为什么这么特殊？
为了得到这个龙形图案，我们需要特殊的方程。它们作用于从点0到点1的一条水平线段，并且映射到两个线段，如下图所示：

随着不断重复，我们得到更多的线段，形成更多的奇妙曲线。

但如果我们想要的是复平面中的某些有趣的集合，我们不需要使用这些特殊的方程。最重要的是这些方程是连续的，意味着它们减少点与点之间的距离。假设用缩写$f_+$和$f_-$，就会有唯一封闭有限集S在这个平面上：

$$S=f_+(S)\cup f_-(S)$$

此外，假设我们从复平面的x点出发，利用$f_+$或$f_-$来作用于它。我们会在S中得到趋向于一个点的序列。甚至更好的情况是S上所有点都类似这样的一个序列的极限。我们甚至可以从相同的x开始来得到它们。具体内容可以参考 John Hutchinson的著名的定理

"有趣，但是系数从1到-1的多项式的根该做什么呢？“你也许会这样想。

我们能可以从数字0开始获得类似这样的多项式，并重复应用到这两个依赖参数z的方程。

$$f_+(x) = 1 + zx$$
$$f_-(x) = 1 - zx$$

例如

$$f_+(0) = 1$$
$$f_+(f_+(0)) = 1+z$$
$$f_-(f_+(f_+(0))) = 1-z(1+z)=1-z-z^2$$
$$f_+(f_-(f_+(f_+(0)))) = 1+ z(1-z-z^2) =1-z-z^2+z^3$$
等等。所有这些多项式有一个共同的常数项：1，不是-1。但是除此以外，我们能利用这个得到系数从1到-1的所有多项式。这样我们得到了总体表达方式，这对我们研究根有很好的帮助。

现在根据z的定义，方程$f_+$和$f_-$会生成不同的龙形集合。我们需要规定|z| < 1来使方程收缩映射。这样就可以得到我所说的龙形的图案。定义$S_z$为依赖变量z的S。

Greg Egan画出了几个集合，下面是其中一个：

这个是一个像羽毛的图案：

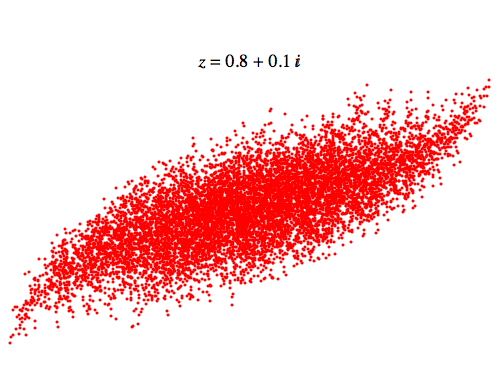
现在有一个十分酷的事实：
在复平面上接近点z，集合Sam Derbyshire画出来有点像广义的龙形集合$S_z$!

”有点像“是模棱两可，因为我不知道精细理论。如果你在看一次Sam的图片：

可以看到在单位圆周围很多”雾霾“，这是$f_+$和$f_-$停止收缩映射。在单位圆外，我暂时不想讨论！但是在单位圆内部，你应该能看到我至少大体正确。例如，如果我们在$z=0.372-0.542i$附近放大，我们得到龙形图案：

至少大体上看起来像这个：

实际上他们应该非常像这个，但是我懒于找点$z=0.372-0.542i$，放大Sam的图片来检查。

类似的，在点$0.8+0.2i$，我们得到羽毛图案：

而且看起来像这个：

如果我能准确的定位点$0.8+0.2i$并且放大观察，会更有说服力。不过我想可以说服Dan Christensen来做这个事情。

还有很多问题要回答，例如”在Sam的图片中间黑色的区域是什么呢？“，以及”在单位圆附近那个看起来很好玩的洞是什么？”但是最迫切问题是：
如果你在Sam Derbyshire画的集合的点z附近放大,为什么会看起来像集合$S_z$?

答案是被“路人”发现的——我们的笔名。这个和Julia-Mandelbrot巧合有关系。我也想解释清楚它，但是我自己也没搞懂。所以我只是拷贝了Greg Egan的解释。

首先，我们定义一个系数从-1到1的李特尔伍德多项式。我们已经看到如果使用任意z，我们可以得到在所有n阶李特尔伍德多项式在x=0处z的图像，并且反复利用如下方程：

$$f_+(x)=1+zx$$
$$f_-(x)=1-zx$$
一共有n+1次。
此外，我们能看到随着我们持续反复在x=0处应用方程，我们得到趋向广义龙形集合$S_z$的序列。

那么,$S_z$是序列的极限的集合，我们通过数字z和越来越高阶的李特尔伍德多项式来得到。

现在，假设0是在$S_z$中，有高阶李特尔伍德多项式作用于z，并趋向于0，我们得到得图像如下：

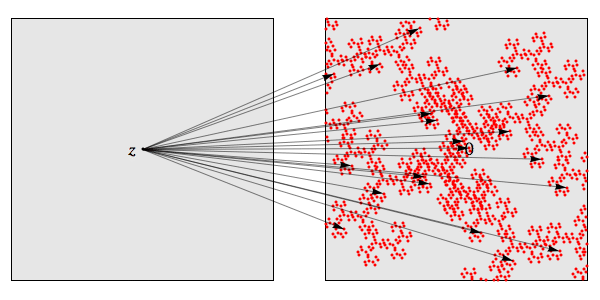
箭头表示不同的李特尔伍德多项式映射到z。如果我们放大足够的程度，线性近似的好，我们能看到在这些多项式下，0的逆向图像是什么样子的：

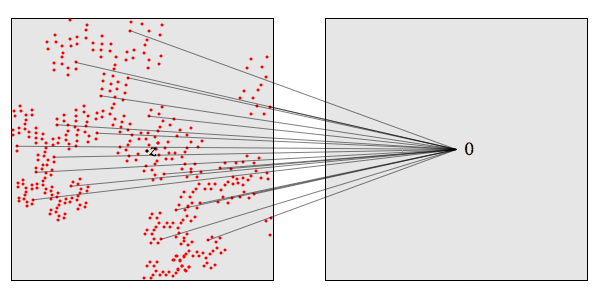
它们看起来是一样的！但是这个逆向图像只是李特尔伍德多项式的根。李特尔伍德多项式在z处的根看起来就像广义龙形集合$S_z$。

Egan写到：
但是如果我们抓取所有的箭头：

并且压缩它们的端点，使它们精确映射到0——并且如果在0附近足够小的区域，箭头实际不会因为被移动而改变——在箭头尾部的图案会很像原始图案：

这有很多要说的，但是我认为可以很快结束。我只是想强调这都是仿照 Mandelbrot 集和Julia 集之间很酷的关系。

考虑这个方程，依赖一个复数参数z：

$$f(x)=x^2+z$$
如果我们固定z，函数定义了一个映射从复平面到它本身。我们可以从任意数字z开始，持续一遍遍的应用这个映射。我们得到一个数列。有时这个数列是发散的，有时候不是。集合的无法到达的边界被称为数字z的julia集合。
另一方面，我们从x=0开始，绘制数字z的集合，其生成序列不会发散。这是Mandelbrot集合。

有一个很酷的关系：在数字z的附近，Mandelbrot集合会来起来像Julia集合，尤其是在Mandelbrot集合边界处。

例如，Julia集合：

$$z=−0.743643887037151+0.131825904205330i$$
看起来：

而这个

是在相同的z处Mandelbrot集合的一小片。他们真的是很相似！

这就是为啥Mandelbrot集合是如此复杂。Julia集合已经十分负责了，但是Mandelbrot集合看起来有很多Julia集合。就像在一个大的人脸照片是有很多很多不同人脸照片组成的一样。

这有个图片可以作为例子，你可以点击看更大的图片看更多的图片：

这个图你真的需要看一下！这是一个由很多各种z值的Julia集合图片组成的大图。你会注意到Mandelbrot集合是连接Julia集合的数字z所组成的集合。Julia集合是黑色的斑点。当z离开Mandelbrot集合，它的Julia集合会坠入到灰尘中：那些白色的部分。

为了更好观察多项式，尝试这个：David Joyce, Mandelbrot and Julia set explorer

你可以放大Mandelbrot集合观察不同变量z下的对应的Julia集合。例如一个Julia集合在$z=−0.689494949−0.462323232i$

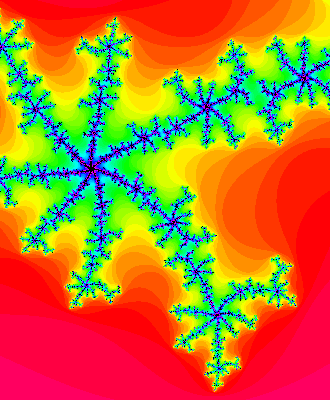
一个点附近的Mandelbrot集合的片段：

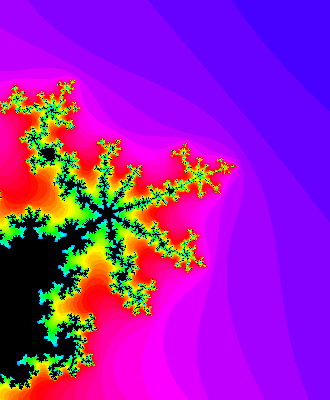
这样来看，Mandelbrot集合就像一个图文并茂的Julia集合的目录。类似的，李特尔伍德多项式的根的集合就像一个广义龙形图案集合的目录。然而，要把这些做成理论需要我做更多的细节的事情，但是我不知道如何做。

更多的相关主题：

• Greg Egan, Littlewood applet. An interactive webpage that lets you explore regions of the Derbyshire set and compare them to the corresponding dragons.

• John Baez, Dan Christensen and Sam Derbyshire, The beauty of roots. (一个主题的幻灯片，有很多好看的图片和本文没有提及的理论）

• John Baez, This Week's Finds in Mathematical Physics (Week 285), n-Category Café, December 6, 2009.
  (本文提到了这个文正，但是这个讨论很有趣！)

• John Baez, The beauty of roots, Azimuth, December 11, 2011.
  (Ditto.)

• Dan Christensen, Plots of roots of polynomials with integer coefficients.

• Loki Jörgenson, Zeros of polynomials with constrained coefficients and related pictures.
• Xiao-Song Lin, Zeros of the Jones polynomial.
• Andrew M. Odlyzko and B. Poonen, Zeros of polynomials with 0,1 coefficients, L'Enseignement Math. 39 (1993), 317-348.
• Eric W. Weisstein, Polynomial roots, from MathWorld.

我的大学同学Xiao-Song Lin 绘制了Jones多项式的零点，有多达13个主要的交点，你可以在上面看到他的图片。你也会在他的图片中看到一些来自Christensen集合的图案，由于Jones多项式已经有整数系数。

Odlyzko和Poonen 提供一些有趣的事情，关于系数从0到1的所有多项式的所有根的集合。如果我们定义一个更精巧的Christensen集$C_{d,p,q}$作为系数从p到q，d阶的所有多项式的所有根的集合，Odlyzko和Poonen在研究当在$d\to\infty$时的$C_{d,0,1}$。他们提到一些已知的结论，并且证明了一些新的：这个集合包含在半平面$Re(z)<3/2$和一个$1/phi＜|z|<\phi \quad \phi= \sqrt5 +1$的环内。事实上，他们不止在这些圆之间，也在两个微妙的曲线之间。这也表达出这个集合是封闭的，是路径连通的，而不仅是简单连通。