Radioactive Decay Problem Involving Two Types Of Nuclei

程熹 2013301020038 物基一班
Homework

---

Abstract

This article discusses the problem that a radioactive decay problem involving two types of nuclei, the two different types of nuclei have different deacy velocity according to the present number of the two nuclei. We use the Euler muethod in this passage to stimulate the number of nucleis changing with the time T.

Key Word

Radioactive decay,two types,euler method.

Introduction

Radioactive decay is a random process at the level of single atoms, in that, according to quantum theory, it is impossible to predict when a particular atom will decay. The chance that a given atom will decay never changes, that is, it does not matter how long the atom has existed. The decay rate for a large collection of atoms, however, can be calculated from their measured decay constants or half-lives. This is the basis of radiometric dating. The half-lives of radioactive atoms have no known lower or upper limit, spanning a time range of over 55 orders of magnitude, from nearly instantaneous to far longer than the age of the universe. A radioactive source emits its decay products isotropically.
Radioactivity is one very frequently given example of exponential decay. The law describes the statistical behaviour of a large number of nuclides, rather than individual atoms. In the following formalism, the number of nuclides or the nuclide population N, is of course a discrete variable (a natural number)—but for any physical sample N is so large that it can be treated as a continuous variable. Differential calculus is needed to set up differential equations for the modelling the behaviour of the nuclear decay.
The mathematics of radioactive decay depend on a key assumption that a nucleus of a radionuclide has no "memory" or way of translating its history into its present behavior. A nucleus does not "age" with the passage of time. Thus, the probability of its breaking down does not increase with time, but stays constant no matter how long the nucleus has existed. This constant probability may vary greatly between different types of nuclei, leading to the many different observed decay rates. However, whatever the probability is, it does not change. This is in marked contrast to complex objects which do show aging, such as automobiles and humans. These systems do have a chance of breakdown per unit of time, that increases from the moment they begin their existence.

Main Features

We use the Euler method to translate the origin equation

$$\frac{d N_{A} }{t}= \frac{ N_{B} }{ \tau _{B} }- \frac{ N_{A} }{ \tau _{A} }$$ $$\frac{d N_{B} }{t}=-\frac{ N_{A} }{ \tau _{A} } - \frac{ N_{B} }{ \tau _{B} }$$ to $$N _{A} (i+1)=N _{A} (i) +\frac{ N_{B} }{ \tau _{B} }dt- \frac{ N_{A} }{ \tau _{A} }dt$$ $$N _{B} (i+1)=N _{B} (i)+\frac{ N_{A} }{ \tau _{A} }dt-\frac{ N_{B} }{ \tau _{B} }dt$$
we can use this equation to design a program to calculate the number of the two different type of nuclei NA and NB changing according to time T,by set different initial condition and different value of the time constant ,we can get completely different population growth curve.

Result

1.a=1000 b=500 time constant=2

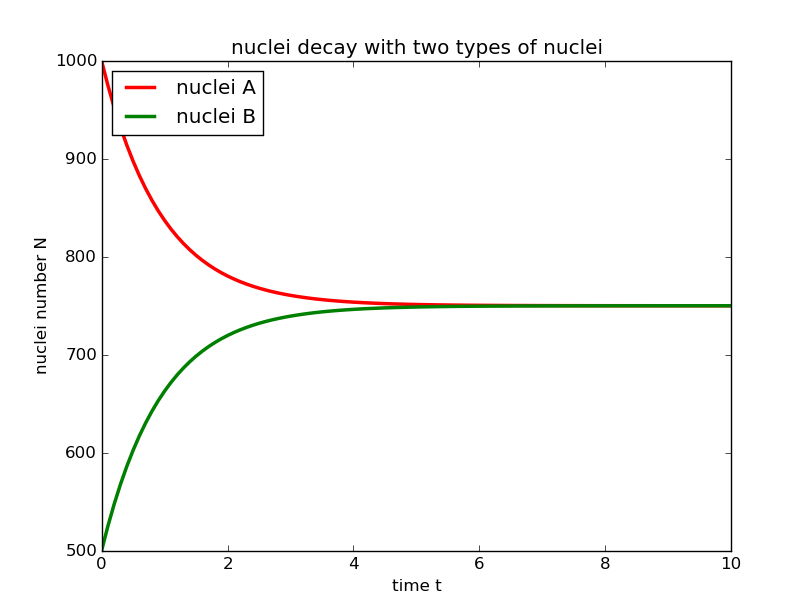
In this condiction, the larger iniital number of nuclei continue to decrease and the smaller initial number of nuclei increase until they reach the same number and then they stay stable.

2.a=1000 b=500 time constant=0.5

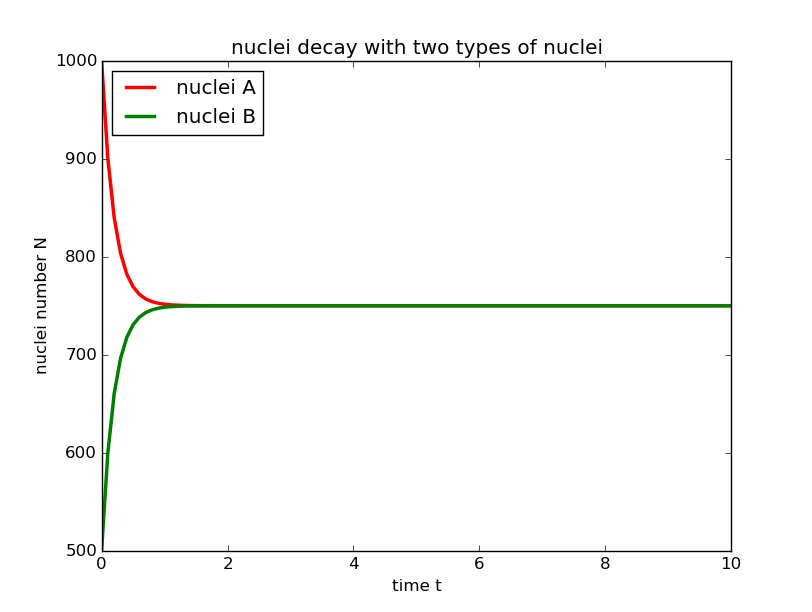
Compare to the first condition, the time constant is smaller, so we can find that the speed of the two types of nuclei reach balanced is faster. So we can infer that the time constant affect the speed of the nuclei decay, the larger the time constant is , the slower the decay is.

3.a=1000 b=0 time constant=2

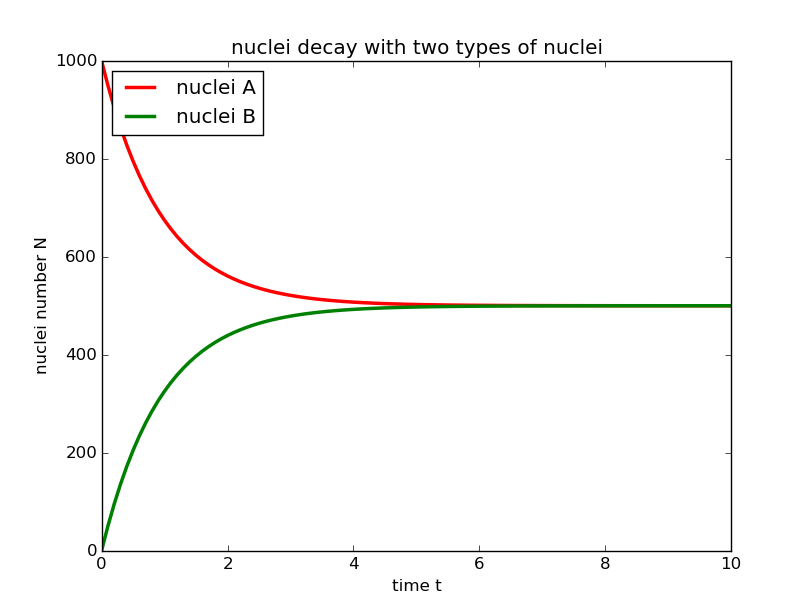
Compare to the first conditon, the initial number of B nuclei is 0,but we can find from the diagram the time it spend to reach balance is the same in the first conditon, the only difference is the balance number of the nucleis, so we can conclude that changing one of the initial number of nuclei won't affect the time to reach balance.

4.a=500,b=0 time constant=2

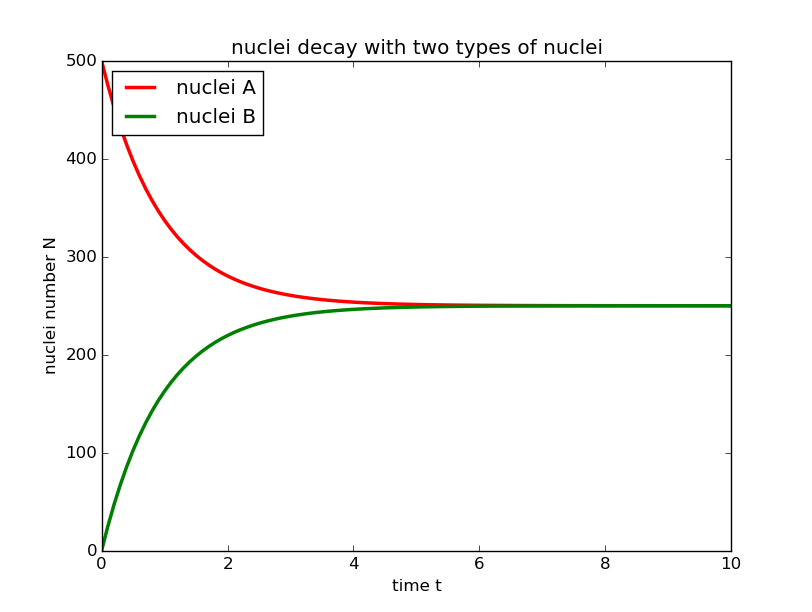
Like in the third conditon, the time to reach the balance hasn't changed, so we are sure that the initial number of the nucleis won't influence the tiem to reach the balance.

Acknowledgement

This program is finished by myself.

Reference

Computational Physics(second edition) Nicholas J.Giordano and Hisao Nakanishi
Wikipedia Radioactive Decay
https://en.wikipedia.org/wiki/Radioactive_decay