The Lorenz Model

程熹 2013301020038
Homework

---

Abstract

This article investigate the Lorenz model used to describe the Earth's atmospheric,we slightly change the initial condition and then we will find the result of the system will change a lot. This effect is called the Bufferfly Effect. We will find the relations between the time t versus z and z versus x and y in Lorenz model.

Key Word

Lorenz model,chaos,butterfly effect,euler-cromer method.

Introduction

Two states differing by imperceptible amounts may eventually evolve into two considerably different states . If, then, there is any error whatever in observing the present state—and in any real system such errors seem inevitable—an acceptable prediction of an instantaneous state in the distant future may well be impossible.In view of the inevitable inaccuracy and incompleteness of weather observations, precise very-long-range forecasting would seem to be nonexistent.
The butterfly effect is the concept that small causes can have large effects. Initially, it was used with weather prediction but later the term became a metaphor used in and out of science.
In chaos theory, the butterfly effect is the sensitive dependence on initial conditions in which a small change in one state of a deterministic nonlinear system can result in large differences in a later state. The name, coined by Edward Lorenz for the effect which had been known long before, is derived from the metaphorical example of the details of a hurricane (exact time of formation, exact path taken) being influenced by minor perturbations such as the flapping of the wings of a distant butterfly several weeks earlier. Lorenz discovered the effect when he observed that runs of his weather model with initial condition data that was rounded in a seemingly inconsequential manner would fail to reproduce the results of runs with the unrounded initial condition data. A very small change in initial conditions had created a significantly different outcome.The idea, that small causes may have large effects in general and in weather specifically.

Main Features

In this article, we tanslate the simplified version of the Navier-Stokes eqquation

$$\frac{dx}{dt}= \sigma (y-x)$$ $$\frac{dy}{dt}= -xz+rx-y$$ $$\frac{dz}{dt}= xy-bz$$ into three equations suitable to design a program by Euler model.Then we design a program to investigate the z component z versus time t,component z versus component x and time t versus component z in the Lorenz model. When we change r,We will find the results will changed a lot even if we have only changed r in small scale.When r is large enough, the system will even become chaotic.

Result

1.Variaton of the Lorenz variable as a function of time with r=25

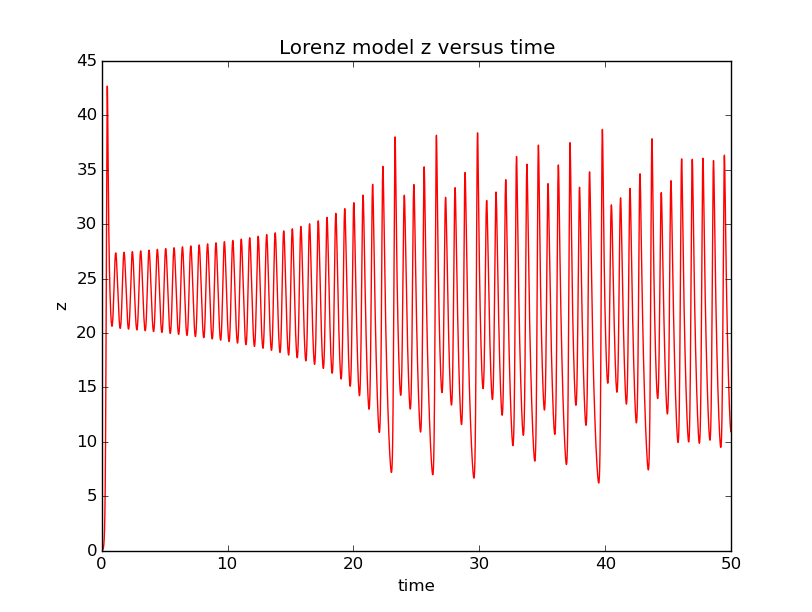
2.Variation of the Lorenz variable as a function of time with r=50

3. Variation of the Lorenz variable as a function of time with r=180

4. Trajectory of the Lorenz model projected onto the x-z plane with r=25

5. Trajectory of the Lorenz model projected onto the x-z plane with r=50

6. Lorent model z versus time with r=160

7. Lorent model z versus time with r=163.8

8. Lorent model z versus time with r=200

Conclusion

1.From the diagram 1 ,diagram 2 and diagram 3 we can find that with the increasing of r, the relation betwee z and t will turn from non-chaos to chaos. For a small r, after a short time the Lorenz variable z will become stable. But when we enlarge r enough, the z will be stable at the beginning of the motion. If we continue to enlarge r, the relationship between r and t will emerge chaos.
2. From the diagram 4 and the diagram 5, we will find that chaos won't energe at a comparable small r.
3. From the diagram 6,diagram 7 and diagram 8, we can conclude that there exist a boundary r, when r is smaller than the boundary, the system can become stable after a while, but when r is greater than the boundary, the the system will become chaos, and the larger the parameter r is , the greater chaos the system will be.

Acknowledgement

This program is finished by myself.

Reference

Computational Physics(second edition) Nicholas J.Giordano and Hisao Nakanishi
Wikipedia Edward Norton Lorenz
https://en.wikipedia.org/wiki/Edward_Norton_Lorenz
Wikipedia Butterfly Effect
https://en.wikipedia.org/wiki/Butterfly_effect