Hindley-Milner类型系统（1）

类型系统 Haskell

---

把类型引入编程语言的主要原因有二：安全性与可读性。

在一门无类型的语言里，并非所有的表达式都是有意义的，比如对一个芒果求平方根。

引入类型系统，是为了确保一个程序的所有表达式都是make sense的。但由于类型系统能力限制，这也会误伤一些本来有意义的表达式。因而会造成如下局面：

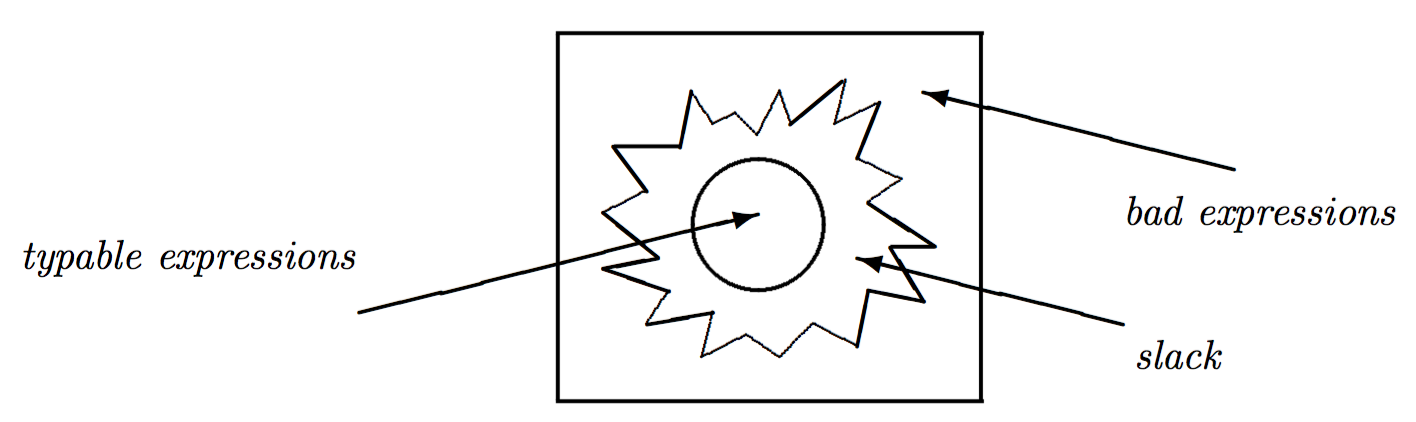
其中slack就是那些被类型系统拒之门外的有意义表达式。

因而，类型系统的设计，是尽可能缩小slack的范围，让尽可能多的有意义表达式能够通过类型系统的检查；同时又能拒绝所有的无意义表达式。

Hindley-Milner类型系统，又称Hindley-Domas-Milner类型系统。目标是在没有任何程序员给出类型注解的情况下，可以自动推导出任意表达式的类型。

语法构造

对于任何一套类型系统，都必须基于一门具体的语言才能给出明确的定义。因而HM类型系统首先定义了一门简单的语言：

$$\begin{align*} e\ \ & = \ x \\ &\ | \ \ \ e_{1}\ e_{2} \\ &\ |\ \ \ \lambda x.e \\ &\ |\ \ \ \mathbf{let}\ x = e_{1}\ \mathbf{in} \ e_{2} \end{align*}$$

从这个定义可以看出，在这本语言里，一切语法构造都是表达式。它一共定义了四种基本的表达式：

1. 变量：$x$
2. 函数调用：$e_{1}\ e_{2}$
3. 函数定义：$\lambda x.e$
4. let绑定：$\mathbf{let}\ x = e_{1}\ \mathbf{in}\ e_{2}$

然后，通过这四种表达式，可以组合成任意复杂度的表达式。

类型

这门语言的类型定义如下：

$$\begin{align*} \tau \ \ & = \ \ \alpha \\ &\ \ |\ \ \ \ \iota \\ &\ \ |\ \ \ \ \tau \rightarrow \tau \\ \sigma \ \ & = \ \ \tau \\ &\ \ |\ \ \ \ \forall \alpha.\sigma \end{align*}$$

在HM类型系统定义里，$\tau$被称做类型（Type），它可以是一个：

• 原生类型：$\iota$
• 类型变量：$\alpha$
• 函数类型：$\tau \rightarrow \tau$

而 $\sigma$ 被称做type scheme。它即可以是一个 $\tau$，即type；也可以是一个$\forall \alpha.\sigma$。而后者，不是type。

之所以说 $\forall\alpha.\sigma$ 不是type，是因为它事实上代表的是一组type的集合。比如：

id :: forall a. a -> a
id x = x

如果没有 $\forall$ 的存在，程序员就必须为每种type都要定义一个特定版本的id函数。比如:

id_Int :: Int -> Int
id_Int x = x
id_Bool :: Bool -> Bool
id_Bool x = x
id_F :: (Int -> Bool) -> (Int -> Bool)
id_F x = x
-- a lot more others ...

而有了 $\forall$ 的帮助，程序员就只需要定义一次。

为了理解$\forall$的语义，我们可以观察下面的两个表达式，然后就会发现它们的相似性:

$$\begin{align*} \forall \alpha &. \alpha \rightarrow \alpha \\ \lambda x &. x\ +\ x \end{align*}$$

你猜的没错，$\forall$ 正是类型系统里的 $\lambda$。

一个形如 $\forall \alpha. \alpha \rightarrow \alpha$ 的 $\lambda$ 在不同的地方被调用（实例化）时，会通过传入不同的 $\alpha$ 而得到不同的类型结果。比如：

$$\begin{align*} (\forall \alpha. \alpha \rightarrow \alpha)\ \textbf{Int}\ \ & \Rightarrow\ \ \textbf{Int} \rightarrow \textbf{Int} \\ (\forall \alpha. \alpha \rightarrow \alpha)\ \textbf{Bool}\ \ & \Rightarrow\ \ \textbf{Bool} \rightarrow \textbf{Bool} \\ (\forall \alpha. \alpha \rightarrow \alpha)\ (\textbf{Int} \rightarrow \textbf{Bool})\ \ & \Rightarrow\ \ (\textbf{Int} \rightarrow \textbf{Bool}) \rightarrow (\textbf{Int} \rightarrow \textbf{Bool}) \end{align*}$$

$\forall$ 可被看作类型世界的 $\lambda$。

由此我们可以看出，虽然 $\forall$ 节省了程序员的重复性工作，但并没有改变这件事的性质：针对每个具体类型，$\forall$ 版本的id定义，都依然会实例化为对应具体类型的版本。

而这正是参数化多态的语义定义。

PolyType & MonoType

理解了polytype的语义之后，我们就可以用一套新的词汇来谈论如下类型体系：

$$\begin{align*} \tau \ \ & = \ \ \alpha\ \ |\ \ \iota \ \ |\ \ \tau \rightarrow \tau \\ \sigma \ \ & = \ \ \tau\ \ |\ \ \forall \alpha.\sigma \end{align*}$$

• $\forall \alpha. \sigma$，之前没有名字，现在被称为多态类型（polytype）；
• 相应的，$\tau\ $，之前我们称做type，现在改称为单态类型（monotype）；
• 然后，我们就可以把type scheme称做类型（type）。

monotype，其中mono是monomorphism的缩写，指单态映射。因而，monotype被称做单态类型。很容易理解，如下类型都属于monotype：

$$\begin{align*} & \textbf{Int} \\ & \textbf{Bool} \\ & \textbf{Bool} \rightarrow \textbf{Int} \\ & (\textbf{Int} \rightarrow \textbf{Bool}) \rightarrow \textbf{Bool} \end{align*}$$

可是，按照 $\tau$ 的定义，如下类型也都属于monotype：

$$\begin{align*} & \alpha \\ & \alpha \rightarrow \beta \\ & (\alpha \rightarrow \textbf{Int}) \rightarrow \beta \end{align*}$$

而我们又知道，如下代码定义了一个多态类型的函数。在其类型注解中，使用的全是类型变量。那么类型变量究竟意味着是单态还是多态？

f :: (a -> b) -> a -> b
f g x = g x

不变的变量

为了理解这个问题，我们再次回到$\lambda$的世界。

在$\lambda$的世界里，操作的是数值（Data Value）。比如1, 2, 0, True, False。这些值，一般被称做literal constant。

除了这些明确的数值，我们还会引入数据变量，简称变量。比如$x, y, z$。

由于Pure FP的不变性，当我们在表达式中使用这些变量时，我们清楚的知道，这些变量对应着一个确定的数值，只是这个表达式未被估值之前，我们还暂时不知道它对应的数值而已。而在运行时，一个变量被赋值的过程叫做变量绑定（variable binding），简称绑定。一旦一个变量被绑定，它对应的数值就被确定，再也不会改变。

所以，一个变量和数值之间的映射关系是单态（monomorphism）的。

而，一个$\lambda$是是一个从数值到数值的映射，不同的输入值，可会能导致不同的输出值。因而，一个$\lambda$和数值之间的关系是多态。

而既然 $\forall$ 是类型世界的 $\lambda$，类型变量也具备相同的性质：当我们看到一个类型变量时，或许还不知道其对应的具体类型是什么，但我们清楚的知道，那个具体类型确定存在，并且不会变化。

而上述例子里函数f的类型，其实是个polytype。虽然程序员无需标注，但编译器会自动补上 $\forall$ 。如下：

f :: forall a b. (a -> b) -> a -> b
f g x = g x

f的类型是一个polytype，但其中的任何类型变量都是monotype。虽然 $a$ 在类型 $\forall a\ b. (a \rightarrow b) \rightarrow a \rightarrow b$ 里出现了两次，但它们所映射的类型必然相同。变量 $b$ 也一样。

现在，我们可以得出如下结论：

在HM类型系统里，所有的类型变量都是单态类型（monotype）。

$\lambda$ 和 $\Lambda$

我们知道，$\lambda$是数值计算的函数：给定一个数值作为参数，产生一个数值作为结果。

类型是比数值更加高阶的领域：每个数值，都至少对应一个类型；而每个类型都有一组数值作为其取值范围。

在数值领域，我们将数值当作计算目标，定义了一套$\lambda$演算系统；而在类型领域，也有一套自己的lambda演算系统，其计算的对象是类型。类型系统的lambda，被称做type lambda，使用符号$\Lambda$进行表示。

Simple-Typed Lambda系统是不需要 $\Lambda$ 的，在那个系统里，类型只被当作数据的一个属性。但是，在更加高阶的polymorphic type lambda系统里，就需要 $\Lambda$ 当作计算类型的函数，类型是其参数和结果。

和 $\lambda$ 一样，$\Lambda$ 也具备 $\alpha$ 变换，$\beta$ 规约，以及 $\eta$ 变换。比如：$\Lambda \alpha.\alpha \rightarrow\alpha$ 与 $\Lambda\beta.\beta\rightarrow\beta$ 完全等价；而 $(\Lambda\alpha.\alpha\rightarrow\alpha)\ \beta=\beta\rightarrow\beta$。

因而，$\lambda$ 和 $\Lambda$ 有着明显的对应关系。比如：

$\lambda$	$\Lambda$
Value	monotype
Literal Constant: 0,1,2,True,False	Primitive: Int,Bool
Variable: $x,y$	Type Variable: $\alpha,\beta$
Variable Binding	Type Variable Binding
Immutable Variable	Immutable Type Variable
Function Application	Type Instantiation
Type	Kind

在$\lambda$演算里，所有的变量都是mono-value，即一个变量和数值之间只能存在一个唯一的映射，一旦绑定，不可变更。

一个类型为整数的变量$x$，与一个数值10并没有任何性质上的不同。在$x + x$里，两个$x$必然具备相同的值。

而对应的，在$\Lambda$里，所有的类型变量也是monotype，即一个变量和类型之间也只能存在唯一的映射，一旦绑定，不可变更。

一个kind为*的变量 $\alpha$，与一个monotype，比如Int, Bool没有任何性质的上的不同。在 $\alpha\rightarrow\alpha$ 里，两个 $\alpha$ 也必然意味着同一类型。

在数值领域，对于已经存在的数值，我们可以进一步进行计算，比如表达式$3 + 5 * 6$，其中，+, *都是 $\lambda$:

(*) :: Int -> Int -> Int
(*) = \x y -> x `valMul` y
(+) :: Int -> Int -> Int
(+) = \x y -> x `valPlus` y

而在类型的世界里，利用已经存在的类型，我们也可以通过计算得到新的类型。比如类型Either Int (Bool,Int)。其中，Either和(,)，它们都是代数数据类型（Algebra DataType）。最有趣的是，它们是$\Lambda$世界的$+$和$\times$:

$$\begin{align*} &\ \ \ \textbf{Either} :: * \rightarrow * \rightarrow * \\ &\ \ \ \textbf{Either} = \Lambda \alpha\ \beta.\ \alpha + \beta \\ &\ \ \ \mathbf{data} \textbf{ Either a b = Left a | Right b} \end{align*}$$

其定义包含三部分：其中第一行是Either的类型（即kind），第二行是Either的实现，这是一个type lambda，第三个则是Either类型的所有数据定义，这也正是为何第三行使用的关键字是data。

当然，在haskell给供给程序员的编程界面里，我们只需要定义第三行，而前两行则是编译器自动帮我们进行推演和实现的。

而$(,)$则实现了类型系统的乘法：

$$\begin{align*} & \textbf{((,))} :: * \rightarrow * \rightarrow * \\ & \textbf{((,))} = \Lambda \alpha\ \beta.\ \alpha \times \beta \\ & \mathbf{data} \textbf{ (a,b) = (a,b)} \end{align*}$$

这也正是在类型系统文献里，会直接用$\times$和$+$来表示$(,)$和Either的原因：

$$\begin{align*} (\textbf{Int}, \textbf{Bool})\ = \ \ (\Lambda \alpha\ \beta. \alpha \times \beta)\ \textbf{Int Bool} \ \ = \ \ \textbf{Int} \times \textbf{Bool} \\ \textbf{Either Int Bool} \ = \ (\Lambda \alpha\ \beta. \alpha + \beta)\ \textbf{Int Bool} \ = \ \textbf{Int} + \textbf{Bool} \end{align*}$$

Either是一个type lambda，而Either Int Bool则是一个从type lambda计算得到的type。同时，Either是一个polytype，而Either Int Bool是一个monotype。因而polytype就是type lambda。

如下是类型系统System F的表达式：

$$\begin{align*} (\Lambda \alpha. \lambda x:\alpha. x) :: \forall \alpha. \alpha \rightarrow \alpha \end{align*}$$

其中，符号$\forall$虽然是一个量词限定符，但从这个表达式可以看出，$\forall$事实上也就可以被看作是$\Lambda$。而haskell的类型系统基本上采用的就是System F。