零基础入门深度学习(9) - Transformer (2/3)

大模型 深度学习入门

---

时隔八年，再次提笔续写这个系列。毫无疑问，智能时代已经到来，AGI（通用人工智能）似乎也不再是遥不可及的梦想。大模型，作为目前最接近实现AGI的技术，甚至已经可以写代码了！这对于程序员真是数十年未有之大变局，因此学好、用好大模型，就将一步跨过JavaScript、Java、C++直接走到鄙视链的顶端，用自然语言编程，成为超级程序员。希望这个系列帮助你快速从零基础达到真入门级水平，理解大模型才能用好大模型。零基础意味着你不需要太多的数学知识，只要会写程序就行了。虽然文中会有很多公式你也许看不懂，但同时也会有更多的代码，程序员的你一定能看懂的（我周围是一群狂热的Clean Code程序员，所以我写的代码也不会很差）。

文章列表

零基础入门深度学习(1) - 感知器
零基础入门深度学习(2) - 线性单元和梯度下降
零基础入门深度学习(3) - 神经网络和反向传播算法
零基础入门深度学习(4) - 卷积神经网络
零基础入门深度学习(5) - 循环神经网络
零基础入门深度学习(6) - 长短时记忆网络(LSTM)
零基础入门深度学习(7) - 递归神经网络
零基础入门深度学习(8) - Transformer(1/3)
零基础入门深度学习(9) - Transformer(2/3)
零基础入门深度学习(10) - Transformer(3/3)

往期回顾

在前面的文章中，我们介绍了全连接神经网络、卷积神经网络、循环神经网络等，可以它们看做是不同结构的神经网络。本文将继续从结构这个角度出发，介绍一种新的、极其重要的神经网络结构：Transformer。从时间来看，它也不是那么新，毕竟是2017年出现的，到现在（2025年）也将近十年了。然而，没有一个更新的网络结构比它还成功，也说明其结构设计是极为优秀的。Transformer出现后，用了5年左右的时间，逐渐取代卷积神经网络成为当红一哥，又用另外5年开辟了一个全新的时代：大模型时代。可以说，目前所有的大模型，都是以Transformer结构为基础的各种变体。如果您刚刚开始学习AI，可以尝试快速跳过Transformer之前的部分，把主要的精力放在Transformer的学习上。

由于Transformer内容较多，为了保持一个良好的节奏，我将整个内容分成三个部分。第一部分比较简单，是一些基础知识的介绍；第二部分重点讲述transformer的注意力机制，这也是它的核心部分；第三部分讲述模型的整体结构，以及训练和推理。

自注意力机制

集中注意力是人类智能中一个非常重要的能力。人类可以从海量的输入信息中，抓住重点的少量信息，忽略掉无用的大量冗余信息，高效完成信息处理，从而达到很高的智能。那么，模型是否可以建立和人类类似的注意力机制，并且从中获益呢？答案是肯定的。

注意力机制的核心，就是提升关键信息的权重，降低非关键信息的权重，通过给每个信息赋予不同的注意力权重，达到聚焦关键信息，忽略非关键信息的效果。下图展示了在视觉处理中，注意力机制的原理：

在图像分类的任务中，重点是对动物进行分类的准确性，与之最相关的图像部分被注意力机制赋予了更高的权重，对分类结果影响举足轻重；图像的背景部分则被注意力机制赋予很低的权重，以至于对最终的分类结果影响极小。这种注意力机制有效的提升了模型分类准确率。

自然语言理解任务则更为复杂一些，因为同样的词在不同的上下文中，其含义是不一样的，例如下面两句话：

The animal didn't cross the street because it was too tired.
The animal didn't cross the street because it was too wide.

显然，两句话中仅仅最后一个单词不同，但导致了代词it 指代的含义不同。在第一句话中，it 指代 animal，而第二句话中，it 指代 street。从注意力机制角度看，显然，第一句话中的it应该更加注意road，而第二句话中的it应该更注意cat。我们希望模型的注意力机制能够达到下面的效果：

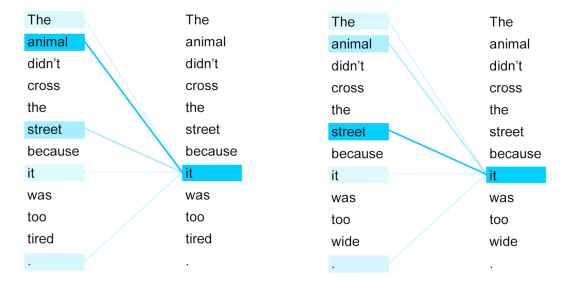
那么，我们应该设计什么样的模型结构，使得每个token可以根据上下文的不同，为每个Token分配不同的注意力权重？这就是Transformer结构核心：自注意力机制（Self-Attention）。其核心是一个序列中的任意两个Token之间都要计算注意力权重，也就是每个Token都要注意自身以及序列中的其它Token，因而叫做自注意力机制。

具体该如何计算呢？为了不失普遍性，我们任意选取序列中的两个Token： $i$ 和 $j$ ，详细介绍他们之间如何计算注意力权重。只要把这个说清楚了，整个序列的注意力计算也就容易理解了。

第一步，需要为每个Token $\mathbf{x}$ 线性投影出三个向量，分别命名为 $\mathbf{q}$ ， $\mathbf{k}$ ， $\mathbf{v}$ 。这三个向量的维度可以和词向量的维度不同， $\mathbf{v}$ 的维度可以和 $\mathbf{q}$，$\mathbf{k}$ 不同。例如，可以设置词向量 $\mathbf{x}$ 维度是 $D_x=512$，$\mathbf{q}$，$\mathbf{k}$ 的维度是 $D_{qk}=128$ ， $\mathbf{v}$ 的维度是 $D_v=256$ 。当然， $\mathbf{x}$ ， $\mathbf{q}$ ， $\mathbf{k}$ ， $\mathbf{v}$ 都设置成同样的维度也没问题，很多模型也都是这样做的。计算 $\mathbf{q}$ ， $\mathbf{k}$ ， $\mathbf{v}$ 很简单，只要经过一次线性映射：

$$\mathbf{q}=W_q\mathbf{x}\\ \mathbf{k}=W_k\mathbf{x}\\ \mathbf{v}=W_v\mathbf{x}$$
其中，$W_q$，$W_k$，$W_v$ 分别是三个权重矩阵，是模型可学习参数的一部分，在模型训练过程中寻找这些参数的最优值。显然，$W_k,W_v \in \mathbb{R}^{D_{kv}\times D_x}$，$W_v \in \mathbb{R}^{D_v\times D_x}$。注意，这里我们按照惯例，用 $\mathbf{x}$ 表示列向量，用 $\mathbf{x}^\mathsf{T}$ 表示行向量。

q, k, v分别是Query、Key、Value的缩写，它们是对注意力机制计算过程的抽象表达，有助于我们理解和实现。

第二步，计算两个Token之间的注意力权重。我们以 $i$ 和 $j$ 为例，这里需要注意的是 $i$ 对 $j$ 的注意力和 $j$ 对 $i$ 注意力是不同的。其实这很容易理解，人与人之间的注意力不也是如此么，黎叔说的好：我本将心向明月，奈何明月照沟渠，大概就是这么一回事。计算方法很简单：

$$a_{ij}=\mathbf{q}_i^T\mathbf{k}_j\\ a_{ji}=\mathbf{q}_j^T\mathbf{k}_i$$

当qk两个向量的维度较大时，点积的数值幅度会显著增大，会导致训练时梯度消失。为缓解这一效应，需要对点积的结果进行缩放。Transformer采用的缩放因子是 $\frac{1}{\sqrt{D_{qk}}}$ ，其中 $D_{qk}$ 是qk向量的维度。

$$a_{ij}=\frac{\mathbf{q}_i^T\mathbf{k}_j}{\sqrt{D_{qk}}}\\ a_{ji}=\frac{\mathbf{q}_j^T\mathbf{k}_i}{\sqrt{D_{qk}}}$$

假设整个序列长度为 $S$，那么，所有Token之间两两计算注意力权重后，我们必然会得到一个注意力矩阵 $A \in S \times S$。即：

$$A=\frac{\mathbf{Q}^T\mathbf{K}}{\sqrt{D_{qk}}}$$

其中， $Q$ 是序列中所有Token的 $\mathbf{q}$ 向量组成的矩阵， $K$ 是序列中所有Token的 $\mathbf{k}$ 向量组成的矩阵。 $Q \in \mathbb{R}^{D_{kv} \times S}$，$Q \in \mathbb{R}^{D_{kv} \times S}$，$A \in \mathbb{R}^{S \times S}$。

第三步，利用Softmax对注意力权重归一化。前面计算出来的注意力权重a是未归一化的，而我们希望归一化，即所有注意力权重都应该是非负数，且加在一起应该等于1，这样注意力权重就等同于概率。例如，对于长度为 $S$ 序列，任意Token $i$会计算得 $S$ 个注意力权重，即它对序列中 $S$ 个Token（包含对其自身）的注意力。我们希望这 $S$ 个注意力权重都是非负值，且加在一起的和正好是1。做法也很简单，只要对权重矩阵 $A$ 按行计算Softmax即可：

$$a_i=Softmax(A[i])$$
其中，$a_i$ 表示权重矩阵A的第i行，$A[i]$ 表示从矩阵 $A$ 中取出第 $i$ 行的分块。

第四步
对序列中的每个Token，按照第三步计算的注意力权重，对序列中所有的v向量计算加权和。例如，对于Token $i$ ，在上一步计算出 $S$ 个注意力权重（保存在A矩阵的第 $i$ 行），用它们来计算所有 $S$ 个 $\mathbf{v}$ 向量的加权和。

$$o_i^\mathsf{T}=A[i]V^\mathsf{T}$$

其中$V \in \mathbb{R}^{D_v\times S}$是所有$v$向量组成的矩阵。

我们可以把整个四个步骤用矩阵计算来表示：

$$\begin{align} Attention(Q,K,V)&=Softmax(\frac{\mathbf{Q}^\mathsf{T}\mathbf{K}}{\sqrt{D_{qk}}})V\\ Q&=W_qX\\ K&=W_kX\\ V&=W_vX \end{align}$$

以上就是自注意力机制，虽然看着复杂，其实也不简单，但相信大家都能理解。如果还不理解，可以再参考下面的示意图。在示意图中，我们设置序列长度 $S=3$，词向量维度 $D_x=4$，$qk$ 向量维度 $D_{qk}=2$，$v$ 向量维度 $D_v=3$。

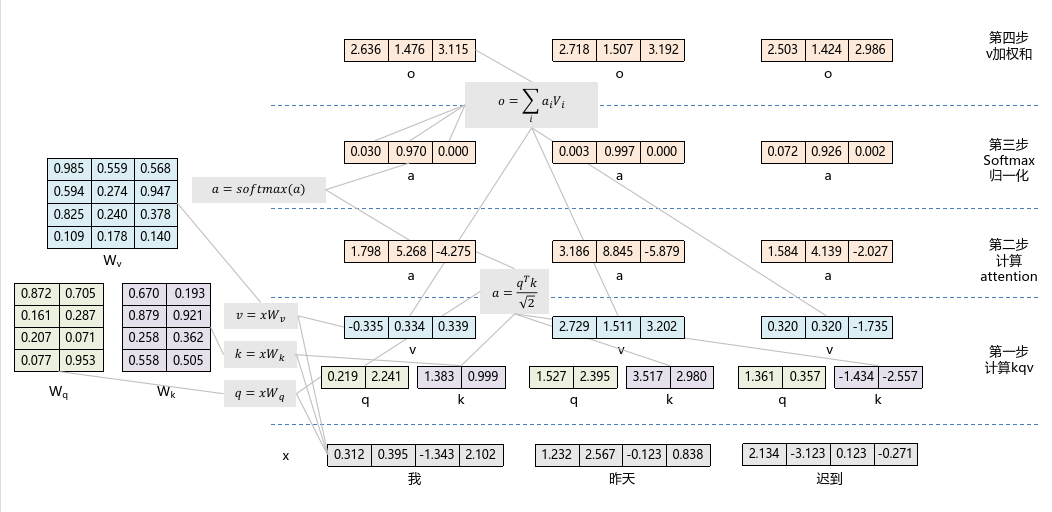
下面自注意力机制的示例代码：

import numpy as np
import math
S=3     # 序列长度
Dq=2    # q向量维度
Dk=2    # k向量维度
Dv=3    # v向量维度
Dx=4    # 词向量维度
def softmax(x, axis=None):
    """数值稳定的 Softmax 实现"""
    e_x = np.exp(x - np.max(x, axis=axis, keepdims=True))  # 减去最大值避免溢出
    return e_x / e_x.sum(axis=axis, keepdims=True)
# 初始化输入词向量矩阵，以及Wq、Wk、Wv三个权重矩阵
X=np.array([[0.312, 0.395, -1.343, 2.102],
       [1.232, 2.567, -0.123, 0.838],
       [2.134, -3.123, 0.123, -0.271]])
Wq=np.random.rand(Dx, Dq)
Wk=np.random.rand(Dx, Dk)
Wv=np.random.rand(Dx, Dv)
def self_attention(X):
    # 计算序列X的self_attention
    # 第一步，计算Q、K、V
    Q=np.dot(X,Wq)
    K=np.dot(X,Wk)
    V=np.dot(X,Wv)
    # 第二步，计算注意力权重
    A=np.dot(Q,K.T)/math.sqrt(Dq)
    # 第三步，归一化注意力权重
    AA=softmax(A, axis=1)
    # 第四步，计算v向量加权和
    O=np.dot(AA, V)
    return O

多头注意力

研究发现，如果仅仅为一个Token线性投影出一份 $D_{qk}$ 的 $\mathbf{q}$、$\mathbf{k}$、$\mathbf{v}$ 向量，那么模型很难关注来自不同语义子空间的信息，因为多个语义子空间的信息被平均化了。解决方法就是多头注意力机制，即为每个Token投影出 $h$ 份不同 $\mathbf{q}$、$\mathbf{k}$、$\mathbf{v}$ 向量，每份 $\mathbf{q}$、$\mathbf{k}$、$\mathbf{v}$ 向量都执行上一章讲述的自注意力函数，并将最终的 $h$ 份输出拼接在一起，再次进行投影，从而得到最终的值，如下图所示。

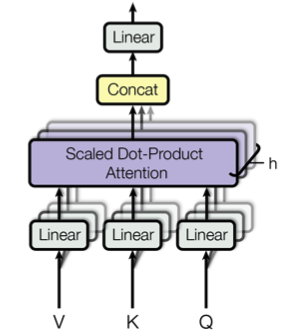
为了不增加计算量和模型参数量，在多头注意力机制中，通常设置每个注意力头的维度是原先的 $1/h$，即 $D_{hqk}=D_{qk}/h$，$D_{hv}=D_{v}/h$。

计算公式为：

$$\begin{align} MultiHead(Q,K,V)&=Concat(head_1,...,head_h)W_o\\ head_i&=Attention(Q_i,K_i,V_i)\\ Q_i&=XW_q^i\\ K_i&=XW_k^i\\ V_i&=XW_v^i \end{align}$$

其中 $W_q^i \in \mathbb{R}^{D_{hqk}\times D_x}$，$W_k^i \in \mathbb{R}^{D_{hqk}\times D_x}$，$W_v^i \in \mathbb{R}^{D_{hv}\times D_x}$，$W_o \in \mathbb{R}^{D_v\times D_x}$。注意，这里设置最终的输出维度为 $D_x$ ，和词向量的维度一致。

因果注意力

文本处理任务通常可以分成文本理解和文本生成两大类，为了便于解释，读者可以简单将其类比为人类的读和写，它们对注意力机制的要求是不同的。对于文本理解任务，可以从前到后、从后到前两个方向对文本进行全面理解，相当于我们在读一篇文章时，可以翻来覆去的正着读、倒着读，这样可以加深对文章的理解（可能您阅读本文时就需要这样）。对于文本生成任务，文本是一个词接着一个词按顺序生成，在生成当前这个词的时候，只能注意到它前面已经生成的词，因为后面的字还没有被生成。相当于我们在写一篇文章时，当前落笔更多的是参考之前写下的内容，因为后面容还没有被写出来，对当前要写的具体内容影响极小（可能只有一个大概的思路）。这样，我们就需要两种不同的注意力机制来对应上述两个不同的过程。对于文本理解，注意力机制设计为双向的，即一个Token既可以注意序列中之前的Token，也可以注意后续的Token。对于文本生成，注意力机制设计为单向的，即一个Token既只能注意序列中之前的Token，不能注意到后续的Token。这种单向的注意力机制，也叫做因果注意力机制。取这个名字，可能是提醒我们不能倒果为因吧。

上一节我们实现的是双向注意力，这一节我们介绍单向注意力的实现方法。单向注意力机制可以用过掩码实现，设输入序列长度为 $S$，掩码矩阵 $M \in \mathbb{R}^{S \times S}$ 的元素定义为：

$$M_{ij} = \begin{cases} 0, & \text{if } i \geq j \quad (\text{允许当前和历史位置交互}) \\ -\infty, & \text{if } i < j \quad (\text{禁止未来位置交互}) \end{cases}$$
其中：
- $i$ 表示 $\mathbf{q}$ 向量的位置。
- $j$ 表示 $\mathbf{k}$ 向量的位置。

掩码矩阵 $M$ 实际上是一个上三角矩阵，其具体形式为：

$$M = \begin{bmatrix} 0 & -\infty & -\infty & -\infty \\ 0 & 0 & -\infty & -\infty \\ 0 & 0 & 0 & -\infty \\ 0 & 0 & 0 & 0 \end{bmatrix}$$

在计算注意力权重时，掩码通过加法融入注意力矩阵：

$$Masked(A) = A + M$$

经过掩码后，Softmax仅对有效位置（ $i\geq j$ ）归一化。因果注意力计算公式为：

$$CausalAttention(Q, K, V) = \text{Softmax}\left( \frac{QK^T}{\sqrt{d_k}} + M \right) V$$

以下是实例代码：

import numpy as np
def causal_attention(Q, K, V):
    """
    实现Transformer Decoder的因果注意力机制
    参数:
    query (np.ndarray): 查询矩阵，形状为 [S, dq]
    key (np.ndarray): 键矩阵，形状为 [S, dk]
    value (np.ndarray): 值矩阵，形状为 [S, dv]
    返回:
    np.ndarray: 注意力输出，形状为 [S, dv]
    """
    # 获取维度信息
    d_k = query.shape[1]
    seq_len = query.shape[0]
    # 生成因果掩码矩阵 M
    mask = np.triu(np.ones((seq_len, seq_len)), k=1)
    mask = np.where(mask == 0, 0.0, -1e9)  # 无效位置设为极大负数
    # 计算原始注意力矩阵
    attn = np.dot(query, key.T) / np.sqrt(d_k)
    # 应用掩码
    masked_attn = attn + mask
    # Softmax归一化
    attention_weights = np.exp(masked_attn) / np.sum(np.exp(masked_attn), axis=1, keepdims=True)
    # 计算加权和
    output = np.dot(attention_weights, value)
    return output

按位置前馈网络

自注意力机制可以看做Token与Token之间的信息混合，那么，Token内部各个维度（通道）也可以做信息混合，类似卷积神经网络中卷积核的大小为1时起到的效果。

该部分由两个全连接层组成，中间采用ReLU激活函数链接，如下图所示：

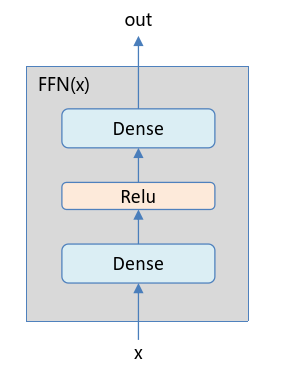
计算公式为：

$$FFN(x) = max(0, xW_1+b_1)W_2+b_2$$

其中，$W_1$、$b_1$、$W_2$、$b_2$ 都是模型的可学习参数。令 $W_i$ 表示中间维度，则$W_1 \in \mathbb{R}^{D_x \times D_i}$，$b_1 \in \mathbb{R}^{D_i}$，$W_2 \in \mathbb{R}^{D_i \times D_x}$，$b_2 \in \mathbb{R}^{D_x}$。中间维度通常设置为输入维度的4倍，即 $D_i = 4D_x$。

以下是示例代码：

import numpy as np
# 维度定义
S = 3          # 序列长度
Dx = 4         # 输入维度
Di = 4 * Dx    # 中间维度
# 初始化权重参数
W1 = np.random.randn(Dx, Di) * 0.01  # 第一隐藏层权重
b1 = np.zeros(Di)                          # 第一隐藏层偏置
W2 = np.random.randn(Di, Dx) * 0.01   # 输出层权重
b2 = np.zeros(Dx)                       # 输出层偏置
def FFN(x):
    """
    前向传播实现位置前馈网络
    输入形状：(S, Dx)
    输出形状：(S, Dx)
    """
    # 将二维输入转换为一维 (S, Dx)
    x_flat = x.reshape(-1, x.shape[-1])
    # 计算第一个线性变换 + ReLU激活
    h = np.maximum(0, np.dot(x_flat, W1) + b1)
    # 计算第二个线性变换
    output_flat = np.dot(h, W2) + b2
    # 恢复原始三维形状
    output = output_flat.reshape(S, -1)
    return output

小节

本文介绍了Transformer的核心：注意力机制。Transformer通过注意力机制实现了Token间信息混合，又通过按位置前馈网络实现了Token内不同通道信息的融合，从而为模型提供了丰富的表达能力。至此，Transformer模型结构的关键元素都已经介绍完了。下一篇文章，我们将介绍Transformer模型及其训练和推理方法，看看是如何将这些要素整合为一个强大的模型。

参考资料

1. Attenion Is All You Need