二叉树的常见算法1

1. 二叉树的存储结构

struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

2. 根据字符串创建一颗二叉树

1. 描述

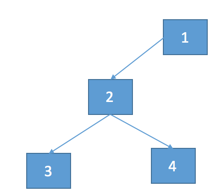
给你一串字符串，每个节点用‘,’隔开，用‘#’代表空的字符串。按从上到下的顺序给出字符串。
例如：
字符串---1,2,#,3,4 对应的二叉树为：

2. 思路

1. 根据‘,’的位置分离出每一个节点，存储在vector数组中。
2. 建立每一个节点的指针关系。
   

3. 代码

TreeNode* Deserialize(string s) {
    if (s.size() == 0) return NULL;
    vector<TreeNode*> path; // 用来存储每个树节点
    while (s != "") {
        int i = 0;
        while (i < s.size() && s[i] != ',') i++;
        string tmp = s.substr(0, i); // 分离出一个节点
        if (tmp == "#") {
            TreeNode* p = NULL;
            path.push_back(p);
                                    
        }
        else {
            int val = atoi(tmp.c_str()); // 将字符串转换成整型
            TreeNode* p = new TreeNode(val);
            path.push_back(p);
                                    
        }
        if (i >= s.size() - 1) s = "";
        else s = s.substr(i + 1);                       
    }
    int index = 1, i = 0; 
    // index记录的是i的子树的位置
    while (index < path.size()) {
        if (path[i] != NULL) {
            if (index < path.size()) path[i]->left = path[index++];
            if (index < path.size()) path[i]->right = path[index++];                    
        }
        i++;    
    }
    return path[0];     
}

3. 将二叉树还原成字符串

描述

题2的镜像问题，给你一颗二叉树，将其还原成字符串。
这里我是按层次遍历的方法写的，如果有疑问，可以转到层次遍历二叉树

string Serialize(TreeNode *root) {
    string ans;
    if (root == NULL) return &ans[0];
    queue<TreeNode *> Q;
    Q.push(root);
    while (!Q.empty()) {
        TreeNode *node = Q.front();
        Q.pop();
        if (node == NULL) ans += ",#";
        else {
            Q.push(node->left);
            Q.push(node->right);
            string tmp = to_string(node->val);
            ans += "," + tmp;       
        }
    }
    int i = ans.size()-1;
    while(i >= 0) { // 去除字符串末尾的#字符
        if (ans[i] == '#' || ans[i] == ',') 
            i--;
        else {
            break;
        }
    }
    return ans.substr(1,i);     
}

4.二叉树的前序遍历（递归+非递归）

1. 递归方法

前序遍历的访问顺序是 根 -> 左 -> 右

void preorder(TreeNode *root, vector<int> &ans) {
    if (root != NULL) {
        ans.push_back(root->val);
        preorder(root->left,ans);
        preorder(root->right,ans);
    }
}

2. 非递归方法

利用栈的FIFO性质，先访问栈的顶层节点，然后先把当前节点的右子树入栈，再把当前节点的左子树入栈。当栈不为空的时候继续访问栈。

void preorder2(TreeNode *root, vector<int> &ans) {
    if (root == NULL) return;
    stack<TreeNode *> S;
    S.push(root);
    // 利用栈的FIFO性质，先将节点的右子树入栈，再将节点的左子树入栈
    while(!S.empty()) {
        TreeNode *node = S.top();
        S.pop();
        ans.push_back(node->val);
        if (node->right) S.push(node->right);
        if (node->left) S.push(node->left);
    }
}

5. 二叉树的中序遍历

1. 递归方法

中序遍历的访问顺序： 左 -> 根 -> 右

void inorder(TreeNode *root,vector<int> &ans) {
    if (root != NULL) {
        inorder(root->left,ans);
        ans.push_back(root->val);
        inorder(root->right, ans);
    }
}

2. 非递归方法

对于任一结点，优先访问其左孩子，而左孩子结点又可以看做一根结点，然后继续访问其左孩子结点，直到遇到左孩子结点为空的结点才进行访问，然后按相同的规则访问其右子树。

 对于任一结点P，

1. 若其左孩子不为空，则将P入栈并将P的左孩子置为当前的P，然后对当前结点P再进行相同的处理；
2. 其左孩子为空，则取栈顶元素并进行出栈操作，访问该栈顶结点，然后将当前的P置为栈顶结点的右孩子；
3. 直到P为NULL并且栈为空则遍历结束

void inorder2(TreeNode *root,vector<int> &ans) {
    if (root == NULL) return;
    stack<TreeNode *> S;
    TreeNode *p = root;
    while(p != NULL || !S.empty()) {
        while (p) {
            S.push(p);
            p = p->left;
        }
        if (!S.empty()) {
            p = S.top();
            S.pop();
            ans.push_back(p->val);
            p = p->right;
        }
    }
}

6. 二叉树的后序遍历

1. 递归方法

后序遍历的访问顺序： 左 -> 右 -> 根

void postorder(TreeNode *root,vector<int> &ans) {
    if (root != NULL) {
        postorder(root->left,ans);
        postorder(root->right, ans);
        ans.push_back(root->val);
    }
}

2. 非递归方法

要保证根结点在左孩子和右孩子访问之后才能访问，因此对于任一结点P，先将其入栈。如果P不存在左孩子和右孩子，则可以直接访问它；或者P存在左孩子或者右孩子，但是其左孩子和右孩子都已被访问过了，则同样可以直接访问该结点。若非上述两种情况，则将P的右孩子和左孩子依次入栈，这样就保证了每次取栈顶元素的时候，左孩子在右孩子前面被访问，左孩子和右孩子都在根结点前面被访问。
参考海子的博客：博客地址

void postorder2(TreeNode *root,vector<int> &ans) {
    if (root == NULL) return;
    TreeNode *cur,*pre = NULL;
    stack<TreeNode *> S;
    S.push(root);
    while(!S.empty()) {
        cur = S.top();
        //如果当前结点没有孩子结点或者孩子节点都已被访问过
        if ( (!cur->left && !cur->right) || ( pre && (pre == cur->left || pre == cur->right))) {
            ans.push_back(cur->val);
            S.pop();
            pre = cur;
        }
        else { // 否则，右子树先入栈，接着左子树入栈
            if (cur->right) S.push(cur->right);
            if (cur->left) S.push(cur->left);
        }
    }
}