算法概论实验六

算法概论实验

实验六
实验目的与要求：掌握动态规划方法的基本思想与设计策略。
1．最长公共子序列问题
【问题描述】
⑴ 给定两个字符串X和Y，设计一个动态规划算法，求出这两个字符串的最长公共子序列，并输出该子序列。
⑵ 若仅要求求出两个字符串的最长公共子序列的长度值，为节省存储空间，采用“滚动数组”方式实现动态规划算法。
2．0-1背包问题
【问题描述】
给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为W（假定物品重量与背包容量值均为整数），应如何选择装入背包中的物品，使得装入背包中物品的总价值最大？设计一个动态规划算法，求解背包问题。

The LCS Question

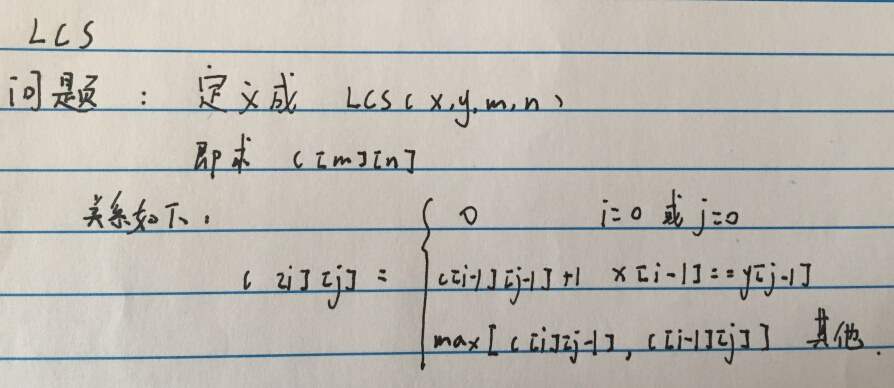
// ConsoleApplication2.cpp : 定义控制台应用程序的入口点。
// VS2013 CPP CODE
//
#include "stdafx.h"
#include<iostream>
using namespace std;
void PrintLcsPath(int ** b, char * x, int m, int n)
{
    if (m == 0 | n == 0)
        return;
    if (b[m][n] == 1)
    {
        PrintLcsPath(b, x, m - 1, n - 1);
        cout << x[m - 1];
    }
    else if (b[m][n] == 2)
        PrintLcsPath(b, x, m, n - 1);
    else
        PrintLcsPath(b, x, m - 1, n);
}
void print(int ** a, int m, int n)
{
    for (int i = 0; i < m + 1; i++)
    {
        for (int j = 0; j < n + 1; j++)
            cout << a[i][j] << "  ";
        cout << endl;
    }
}
int LcsLength(char *x, char *y, int m, int n)
{
    //创建一个 m+1 * n+1 用于存储LCS
    int **a = new int *[m + 1];
    for (int i = 0; i < m + 1; i++)
        a[i] = new int[n + 1];
    //创建一个 m+1 * n+1 用于存储状态
    //来自于对角线 1 来自于左侧2 来自于上方3
    int **b = new int *[m + 1];
    for (int i = 0; i < m + 1; i++)
        b[i] = new int[n + 1];
    //base case
    for (int i = 0; i < m + 1; i++)
        a[i][0] = 0;
    for (int i = 0; i < n + 1; i++)
        a[0][i] = 0;
    //for
    for (int i =1; i < m + 1;i++)
    {
        for (int j =1; j < n + 1;j++)
        {
            if (x[i-1]==y[j-1])
            {
                a[i][j] = a[i - 1][j - 1] + 1;
                b[i][j] = 1;
            }
            else
            {
                if (a[i-1][j] <= a[i][j-1])
                {
                    a[i][j] = a[i][j - 1];
                    b[i][j] = 2;
                }
                else
                {
                    a[i][j] = a[i - 1][j];
                    b[i][j] = 3;
                }
            }
        }
    }
    /*print(a, m, n);
    cout << endl;
    print(b, m, n);*/
    cout << "LCS为：";
    PrintLcsPath(b, x, m, n);
    cout << endl;
    return a[m][n];
}
int main()
{
    char x[] = "12312312qwe12312";
    char y[] = "abqweqw123e123123qwcbdab";
    int m = strlen(x);
    int n = strlen(y);
    cout << "LCS的长度为：" << LcsLength(x, y, m, n) << endl;
}

0-1背包

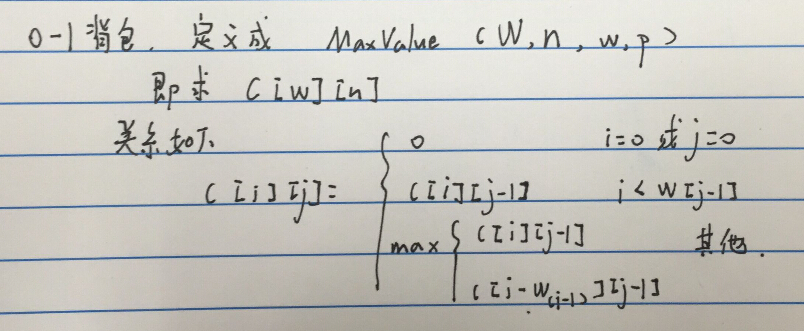
// N给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为W（假定物品重量与背包容量值均为整数），应如何选择装入背包中的物品，使得装入背包中物品的总价值最大？设计一个动态规划算法，求解背包问题。
//
#include "stdafx.h"
#include <iostream>
using namespace std;
#define W 50
void print(int ** a, int m, int n)
{
    for (int i = 0; i < m + 1; i++)
    {
        for (int j = 0; j < n + 1; j++)
            cout << a[i][j] << "  ";
        cout << endl;
    }
}
void Trackback(int *weight, int n, int w,bool *p,int **a)
{
    if (n==0 || w==0)
        return;
    if (a[w][n]==a[w][n-1])//若和左边的一致，说明没有选最后一个
    {
        p[n - 1] = false;
        Trackback(weight, n - 1, w, p, a);
    }
    else
    {
        p[n - 1] = true;
        Trackback(weight, n - 1, w-weight[n-1], p, a);
    }
}
int getMaxValue(int w, int n, int *price, int * weight )
{
    //创建一个 w+1 * n+1 的二维表
    int **a = new int *[w + 1];
    for (int i = 0; i < w + 1;i++)
    {
        a[i] = new int[n + 1];
    }
    //创建一个数组 记录货物是否取的状态
    bool  *p = new bool[w];
    memset(p, false, sizeof(p));
    //base case
    for (int i = 0; i < w + 1; i++)
        a[i][0] = 0;
    for (int i = 0; i < n + 1; i++)
        a[0][i] = 0;
    //for
    for (int i = 1; i < w + 1;i++)
    {
        for (int j = 1; j < n + 1;j++)
        {
            if (i<weight[j-1])//填写a[i][j]，若当前背包重量小于物品，则不装
            {
                a[i][j] = a[i][j - 1];
            }
            else
            {
                if (a[i][j-1] <= a[i-weight[j-1]][j-1]+price[j-1])
                {
                    a[i][j] = a[i - weight[j - 1]][j - 1] + price[j - 1] ;
                }
                else
                    a[i][j] = a[i][j - 1];
            }
        }
    }
    //print(a,w,n);
    Trackback(weight, n, w, p, a);
    cout << "从左到右是否取件为：";
    for (int i = 0; i < n; i++)
        cout << p[i] << " ";
    cout << endl;
    return a[w][n];
}
int main()
{
    //int price[] = { 1, 2, 3, 4, 7 };
    //int weight[] = { 2, 4, 5, 6, 210 };
    int price[] = { 60, 100, 120 };
    int weight[] = { 10, 20, 30 };
    cout << "背包问题的解是："<<getMaxValue(W, 5, price, weight) << endl;
    return 0;
}