算法概论作业6.16 6.19 6.21 6.14

算法概论作业

6.16

本题目的起始顶点（ home）可以访问多次，而且不必访问所有的顶点。以 B(S j , )来表示在 garage sale 集为 S ，结束位置为 j 的子问题上的最大收益值。注意 j 的前导顶点既可能是某个 garage sale，也可能是 home，于是有Dp方程：

DP方程：

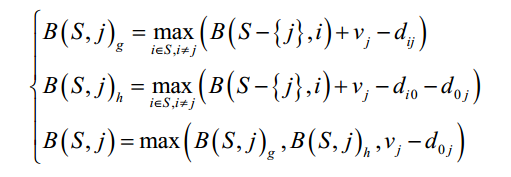
6.19

DP方程：

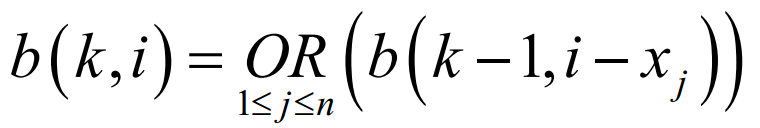
代码如下：

  bool h[K][v];
  int j;
  //initialize
  h[0][0]=true;
  for(j=1;j<=v;j++)
     h[0][j]=false;
  for(j=1;j<=K;j++)
      h[j][0]=false;
  k=0;
 for(j=1;j<=v;j++)
 {
    for(int i=1;i<=n;i++)
    {
        While(k<K)
        {
            if(j==x[i] && k<=K)
            {   h[k][j]=true;   }
            else if(j>x[i] && k<K)
            {   h[k][j]=h[k][j] || h[k-1][j-x[i]];  }
            k++;
        }
    }
 }
 return h[k][v];

6.21

分析：求最小覆盖的大小，即在树中去除最大的独立集，即是最大独立集的补集。

代码如下：

 const int MAXN=100;  
 vector<int> G[MAXN]; //无根树  
 int l[MAXN]; //结点层次  
 int p[MAXN]; //根树  
 int dp[MAXN]; //dp数组  
 int sumC[MAXN]; //孩子DP和  
 int sumS[MAXN]; //孙子DP和  
 int maxL; //最大层次  
 int n;  
 int rootDp(int u)  
 {  
     //构造u根树  
     p[u]=-1;  
     maxL=-1;  
     dfs(u,p[u]);  //遍历
     for(int i=maxL;i>=0;--i)  
     {  
         for(int j=0;j<n;++j)  
         {  
             if(l[j]==i)  
             {  
                 dp[j]=max(sumS[j]+1,sumC[j]);  
                 if(i-1>=0)  
                 {  
                     sumC[p[j]]+=dp[j];  
                 }  
                 if(i-2>=0)  
                 {  
                     sumS[p[p[j]]]+=dp[j];  
                 }  
             }  
         }  
     }  
     return dp[u];  
 }

6.14

每次沿着边沿剪下一块布，这样剩余的布料又可以形成最多三块矩阵面料。设P(w,h),是在宽为 w ，高为 h的布料上所能得到的收益，考虑每一次切割式样的两种情况，于是有DP方程如下

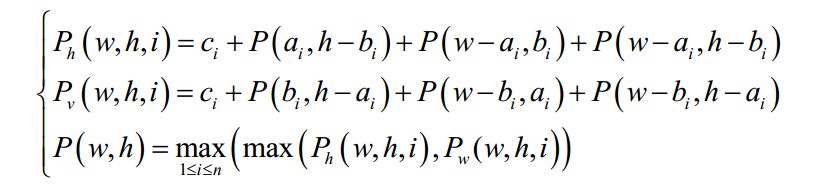
$P_ h(w,h,i)$是将第$i$个式样按照给定的形状直接切下来时的收益，
$P_ v(w,h,i)$ 则是将第$i$个式样按照旋转 90 度后的形状切下来时的收益。
最后返回 $P(x,y)$即可。