CHAOTIC TUMBLING OF HYPERION

未分类

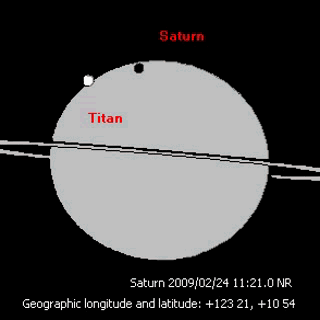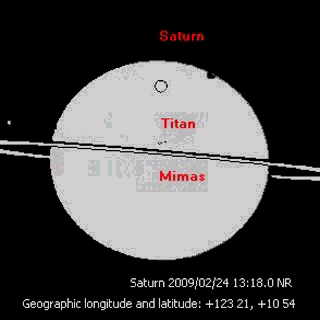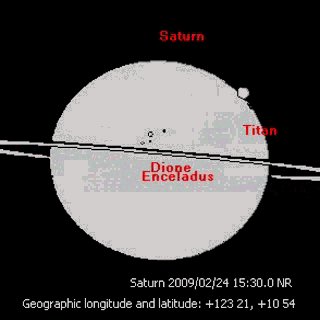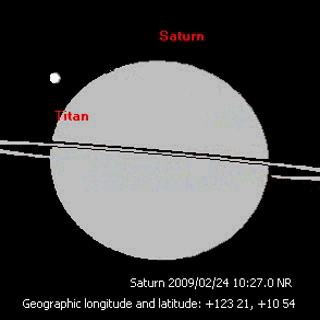
It turns out that all of the moons in the solar system except one exhibit such synchronism.The exception is Hyperion.
The reason for Hyperion's different behavior is its very unusual shape,together with its highly elliptical orbit.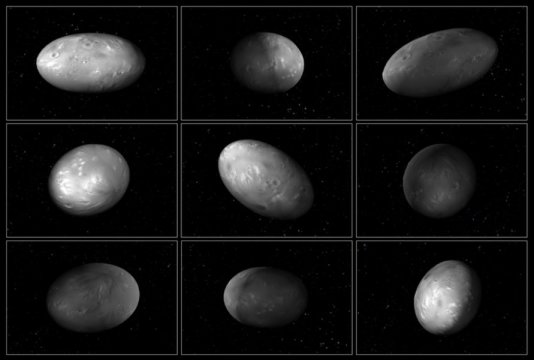
while other moons are approximately spherical,Hyperion is shaped more like an egg.

The simulation of the motion of Hyperion.

To simulate the motion of Hyperion we first make a few simplifying assumptions.Our objective is simply to show that the motion of such an irregularly shaped moon can be chaotic.

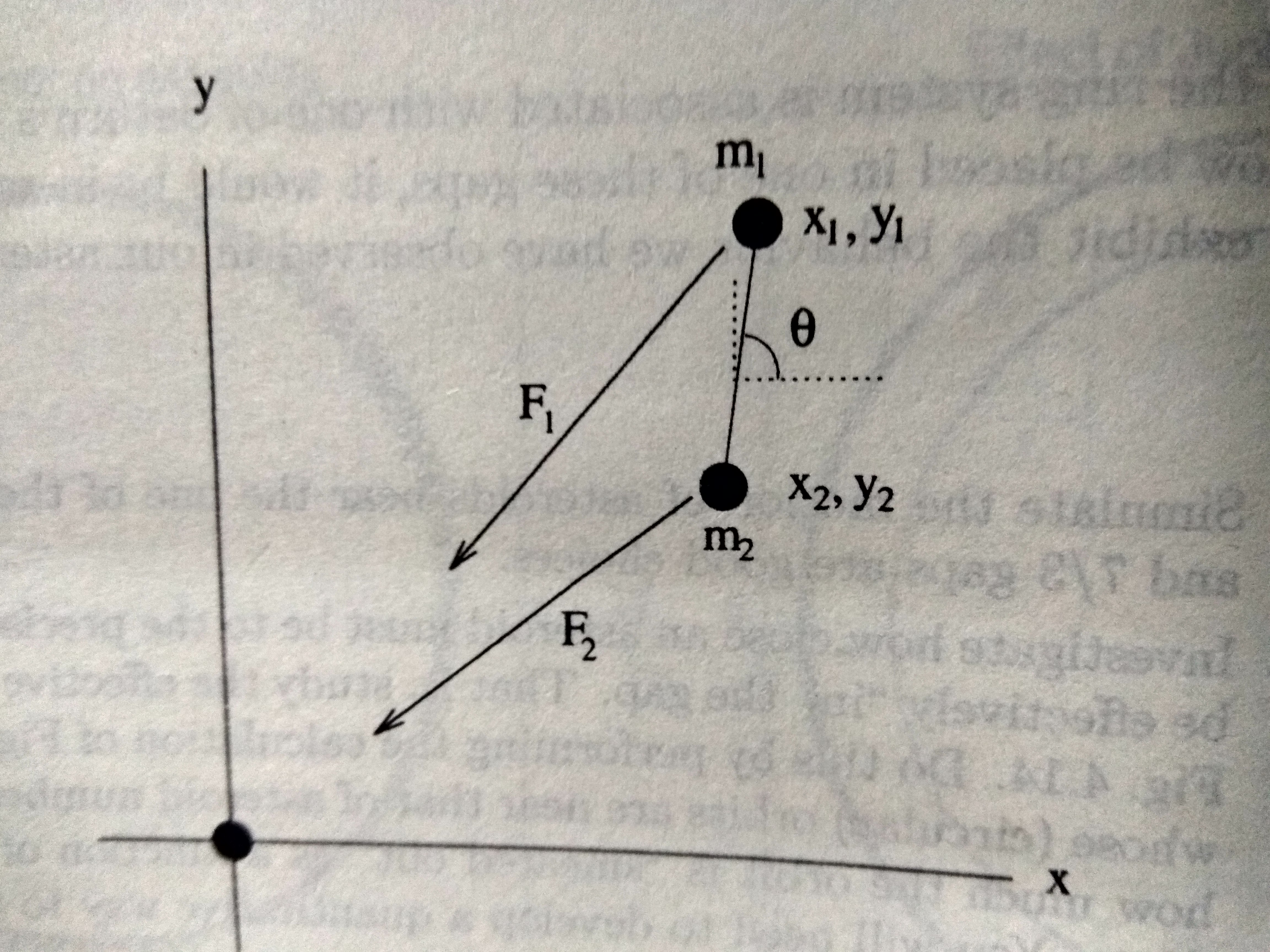
We have two particles,m1 and m2 connected by a massless rod in orbit around a massive object.
There are two forces acting on each of the masses,the force of gravity from Saturn and the force from the rod.Since we are interested in the motion about the center of mass.The gravitational force on m1 can be written as
$\vec{F_1}=-\frac{GM_{Sat}m_1}{r_1^3}(x_1\vec{i}+y_1\vec{j})$
the torque on m1 is then
$\vec{M_1}=[(x_1-x_c)\vec{i}+(y_1-y_c)\vec{j}]×\vec{F_1}$
with a similar expression for$\vec{M_2}$.The total torque on the moon is $\vec{M_1}+\vec{M_2}$
$\frac{d\vec{w}}{dt}=\frac{\vec{M_1}+\vec{M_2}}{I}$
$I=m_1|r_1|^2+m_2|r_2|^2$
$\frac{dw}{dt}≈-\frac{3GM_{Sat}}{r_c^5}(x_csin\theta-y_ccos\theta)(x_ccos\theta+y_csin\theta)$

As for unit,we set
the unit of velicity is the radius of earth
the unit of length is the distance from earth to the sun
the unit of time is the orbital period of the earth around the sun.

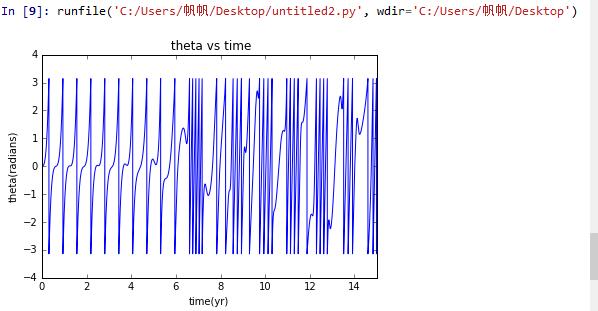
from math import pi,sqrt,sin,cos
import matplotlib.pyplot as plt
def hyperion(theta0):
    # set the mass of saturn
    gm=4*pi**2
    # initialize position of center of mass, angle, angle velocity
    xc=[1]
    yc=[0]
    theta=[theta0]
    avelo=[0]
    vxc=[0]
    vyc=[2*pi]
    # get the trails
    dt=0.0001
    t=[0]
    while t[-1]<=15:
        r=sqrt((xc[-1])**2+(yc[-1])**2)
        vxc_new=vxc[-1]-gm*xc[-1]*dt/r**3
        vyc_new=vyc[-1]-gm*yc[-1]*dt/r**3
        avelo_new=avelo[-1]-12*(pi**2)*(xc[-1]*sin(theta[-1])-yc[-1]*cos(theta[-1]))*(xc[-1]*cos(theta[-1])+yc[-1]*sin(theta[-1]))*dt/r**5
        vxc.append(vxc_new)
        vyc.append(vyc_new)
        avelo.append(avelo_new)
        xc.append(xc[-1]+vxc[-1]*dt)
        yc.append(yc[-1]+vyc[-1]*dt)
        theta_new=theta[-1]+avelo[-1]*dt
        if theta_new<-pi:
            theta_new+=2*pi
        if theta_new>pi:
            theta_new-=2*pi
        theta.append(theta_new)
        t.append(t[-1]+dt)
    return theta,t
t=hyperion(0)[1]
the1=hyperion(0)[0]
the2=hyperion(0.01)[0]
dthe=[]
plt.plot(t,the1)
plt.title(' theta vs time')
plt.xlabel('time(yr)')
plt.ylabel('theta(radians)')
plt.xlim(0,15)
plt.show()

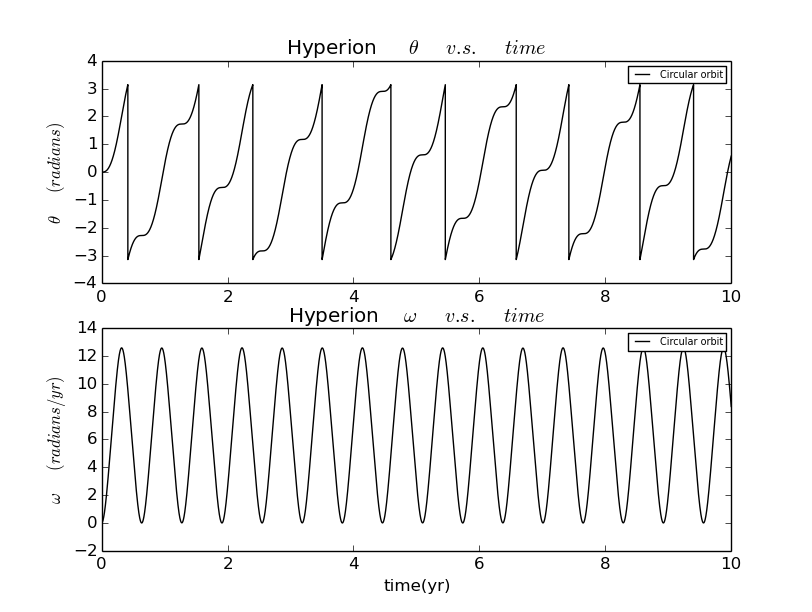
the initial velocity is 2π
the initial velocity is 5

We have therefore calculated the behavior of our model Hyperion for two slightly different initial conditions.
$△\theta=\sqrt{(\theta_1-\theta_2)^2}$
and give a function of time

from math import pi,sqrt,sin,cos
import matplotlib.pyplot as plt
def hyperion(theta0):
    # set the mass of saturn
    gm=4*pi**2
    # initialize position of center of mass, angle, angle velocity
    xc=[1]
    yc=[0]
    theta=[theta0]
    avelo=[0]
    vxc=[0]
    vyc=[5]
    # get the trails
    dt=0.0001
    t=[0]
    while t[-1]<=15:
        r=sqrt((xc[-1])**2+(yc[-1])**2)
        vxc_new=vxc[-1]-gm*xc[-1]*dt/r**3
        vyc_new=vyc[-1]-gm*yc[-1]*dt/r**3
        avelo_new=avelo[-1]-12*(pi**2)*(xc[-1]*sin(theta[-1])-yc[-1]*cos(theta[-1]))*(xc[-1]*cos(theta[-1])+yc[-1]*sin(theta[-1]))*dt/r**5
        vxc.append(vxc_new)
        vyc.append(vyc_new)
        avelo.append(avelo_new)
        xc.append(xc[-1]+vxc[-1]*dt)
        yc.append(yc[-1]+vyc[-1]*dt)
        theta_new=theta[-1]+avelo[-1]*dt
        theta.append(theta_new)
        t.append(t[-1]+dt)
    return theta,t
t=hyperion(0)[1]
the1=hyperion(0)[0]
the2=hyperion(0.01)[0]
dthe=[]
for i in range(len(the1)):
    dthe.append(abs(the2[i]-the1[i]))
plt.plot(t,dthe)
plt.semilogy(t,dthe)
plt.title('delta theta vs time')
plt.xlabel('time(yr)')
plt.ylabel('dtheta(radians)')
plt.xlim(0,15)
plt.show()

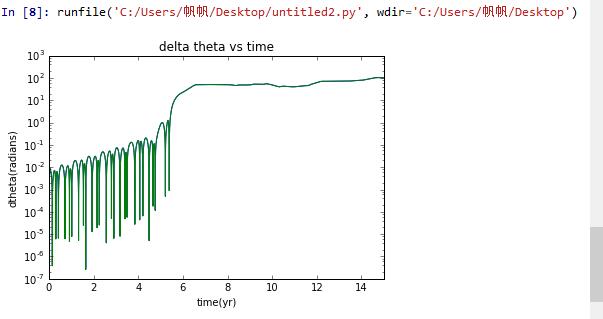
加上对角的束缚($-π=<△\theta<=π$)就是这样的

from math import pi,sqrt,sin,cos
import matplotlib.pyplot as plt
def hyperion(theta0):
    # set the mass of saturn
    gm=4*pi**2
    # initialize position of center of mass, angle, angle velocity
    xc=[1]
    yc=[0]
    theta=[theta0]
    avelo=[0]
    vxc=[0]
    vyc=[5]
    # get the trails
    dt=0.0001
    t=[0]
    while t[-1]<=15:
        r=sqrt((xc[-1])**2+(yc[-1])**2)
        vxc_new=vxc[-1]-gm*xc[-1]*dt/r**3
        vyc_new=vyc[-1]-gm*yc[-1]*dt/r**3
        avelo_new=avelo[-1]-12*(pi**2)*(xc[-1]*sin(theta[-1])-yc[-1]*cos(theta[-1]))*(xc[-1]*cos(theta[-1])+yc[-1]*sin(theta[-1]))*dt/r**5
        vxc.append(vxc_new)
        vyc.append(vyc_new)
        avelo.append(avelo_new)
        xc.append(xc[-1]+vxc[-1]*dt)
        yc.append(yc[-1]+vyc[-1]*dt)
        theta_new=theta[-1]+avelo[-1]*dt
        theta.append(theta_new)
        t.append(t[-1]+dt)
    return theta,t
t=hyperion(0)[1]
the1=hyperion(0)[0]
the2=hyperion(0.01)[0]
dthe=[]
for i in range(len(the1)):
    dthe_new=abs(abs(the2[i]-the1[i]))
    while dthe_new>pi:
        dthe_new-=2*pi
    while dthe_new<-pi:
        dthe_new+=2*pi
    dthe.append(dthe_new)
plt.plot(t,dthe)
plt.semilogy(t,dthe)
plt.title('delta theta vs time')
plt.xlabel('time(yr)')
plt.ylabel('dtheta(radians)')
plt.xlim(0,15)
plt.show()

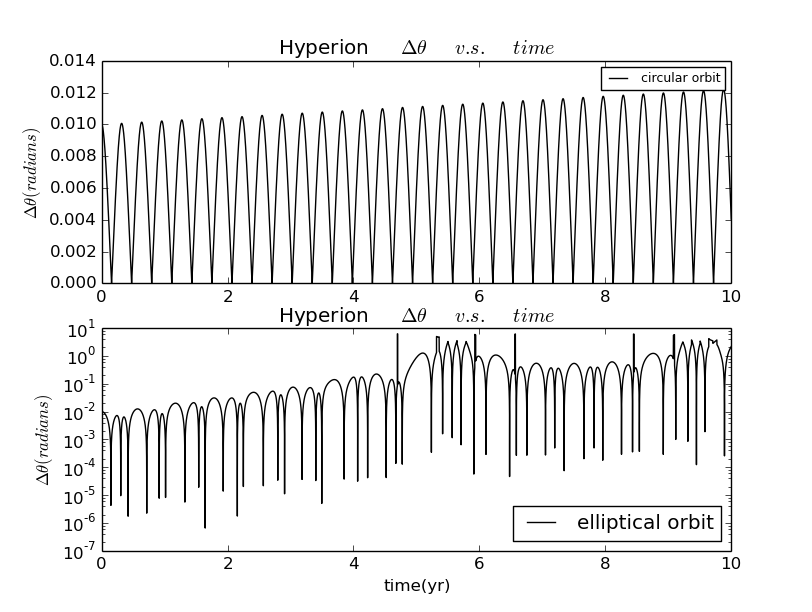
　　　　　　　　for both circular and elliptical orbits

$v_{max}=\sqrt{GM_s\frac{1+e}{a(1-e)}(1+\frac{M_P}{M_S})}$
$v_{min}=\sqrt{GM_s\frac{1-e}{a(1+e)}(1+\frac{M_P}{M_S})}$

here we suppose $M_r/M_s<<1$
while $v_{yo}<2\pi 　　v_{yo}=v_{min}$
$a=\frac{1}{1+e},e=1-{(\frac{v}{2\pi})}^2$
$v_{yo}>2\pi 　　v_{yo}=v_{max}$
$a=\frac{1}{1-e},e={(\frac{v}{2\pi})}^2-1$
and if initial veloxity is $v_{yo}=2\pi$, and then eccentricity e=0,and the Lyapunov exponent is zero.

Now I prepare to choose different initial velocity to change the eccentricity to see how the Lyapunov exponent change.

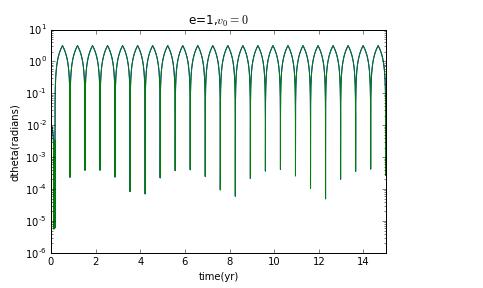
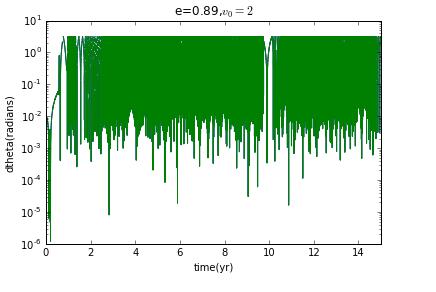
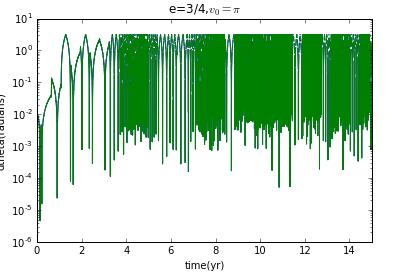
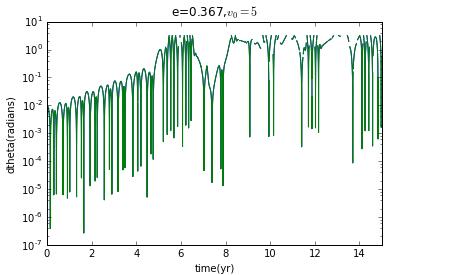
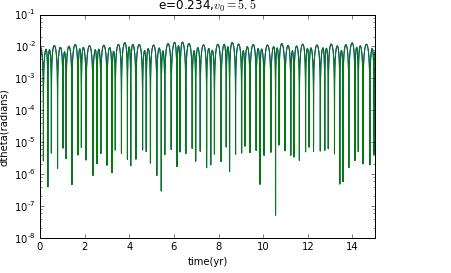
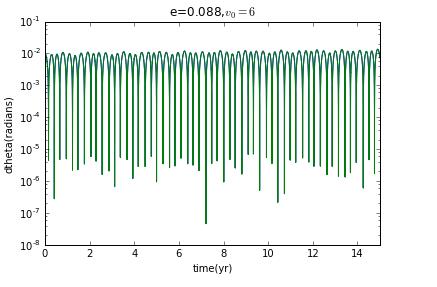
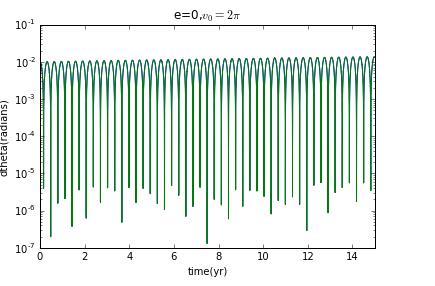
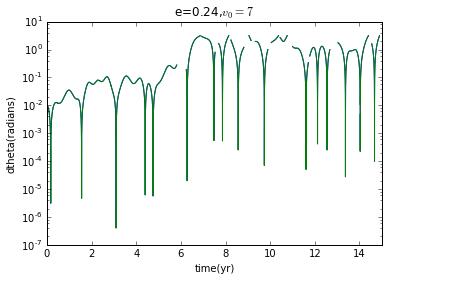
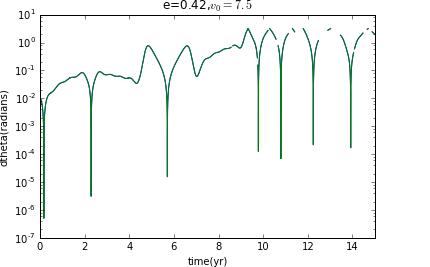
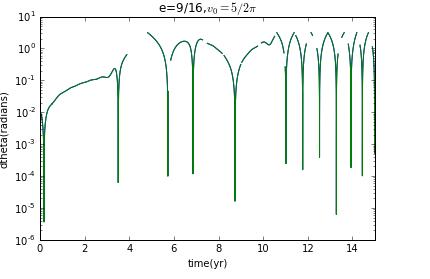
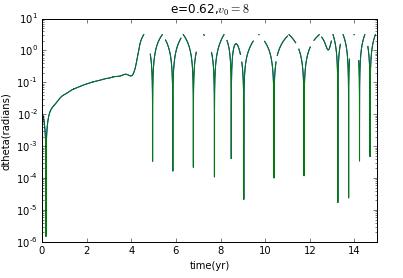
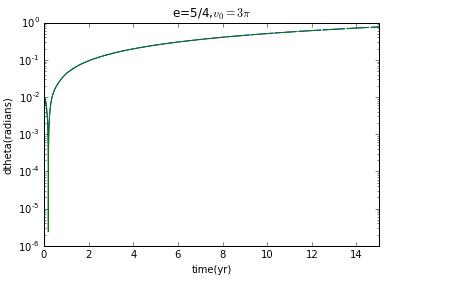
clearly,when it is not ellipse,there is no chaos.

our model for Hyperion is,as we have cautioned,a highly simplified version of the real thing,Our goal was to try to understand the types of motion that are possible,and the results clearly show that such a moon can tumble chaotically.

The dispersion of the distance and eccentricity with deviation angle.

Thanks

Wikipedia
WU yuqiao's partial codes