chap26 最大流

流网络 Ford-Fulkerson方法 最大二分匹配 算法导论

内容

流网络

1. 流网络：

   • $G = (V,E)$, directed.
   • Each edge $(u,v)$; has a capacity $c(u,v)\geqslant 0$
   • If$(u,v) \notin E$, then $c(u,v) = 0$
   • If $(u,v) \in E$, then reverse edge $(v,u) \notin E$. (Can work around this restriction.
   • Source vertex $s$, sink vertex $t$, assume $s\sim v\sim t$for all $t \in V$ , so that each vertex lies on a path from source to sink and $E > V - 1$

2. 流：
   

   

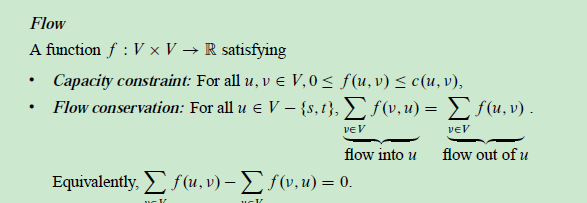
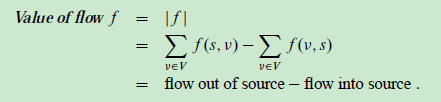
3. 可以通过增加中间结点的方式将不能有反平行边的限制去除，
4. 对于具有对个源结点和汇点的情况，可以加入一个超级源结点和超级汇点来转化成单个源结点和汇点的问题，这两个加入的点的容量都是无穷大

Ford-Fulkerson方法

1. Ford-Fulkerson方法依赖于残存网络、增广路径和切割这三个重要思想，其正确性由最大流最小切割定理保证

2. 残存网络$G_{f}$: 可以看成是去除了反向边限制的流网络，由流网络$G$和流$f$生成

   • 残存容量：$c_{f}(u,v)=\begin{cases} c(u,v)-f(u,v) & \text{ if } (u,v) \in E \\ f(v,u) & \text{ if } (v,u) \in E \\ 0 & \text{ else } \end{cases}$
   • 残存网络的流$f'$,定义：$(f\uparrow f')(u,v) = \begin{cases} f(u,v)+f'(u,v)-f'(v,u) & \text{ if } (u,v) \in E \\ 0 & \text{ else } \end{cases}$，可以证明$f\uparrow f'$是原流网络的一个流，其值为$|f\uparrow f'| = ||f+|f'|$

3. 增广路径：增广路径$p$是残存网络中一条从源结点$s$到汇点$t$的简单路径

   • p的残存容量：$c_{f}(p) = min \{ c_{f}(u,v):(u,v) \in p$
   • 残存网络的一个流$f_{p}$定义为：$f_{p}(u,v) = \begin{cases} c_{f}(p) & \text{ if } (u,v) \in p \\ 0 & \text{ else } \end{cases}$
   • $f \uparrow f_{p}$是$G$的一个流

4. 流网络的切割：切割$(S,T=V-S)$,$s \in S, t \in T$

   • 净流量: $f(S,T) = \sum_{u\in S}\sum_{v\in T}f(u,v) - \sum_{u\in S}\sum_{v\in T}f(v,u)$
   • 容量： $c(S,T) = \sum_{u\in S}\sum_{v\in T}c(u,v)$
   • 由于流量守恒，必然导致:1.所有切割的净流量都等于$|f|$;2.最大流的值不会超过最小切割的容量

5. 最大流最小切割定理：以下条件等价：

   • 1.$f$是$G$的一个最大流
   • 2.残存网络$G_{f}$不包括任何增广路径
   • 3.$|f|=c(S,T)$,其中$(S,T)$是流网络$G$的某个切割

基本的Ford-Fulkerson算法

ford-fulkerson(G,s,t)

for each edge(u,v) in G.E
    (u,v).f = 0
while there exists a path p from s to t in the residual network G_f
    c_f(p) = min{...}
    for each edge(u,v) in p
        if (u,v) in E
            (u,v).f += c_f(p)
        else
            (v,u).f -= c_f(p)

1. 假定所选择的任意增广路径和所有的容量都是整数，如果容量为有理数，可以乘上某个系数转化成整数
2. 若f是某个最大流，则while循环最多|f|次（对应每次流只增加1）
3. 用有向图来表示残差网络，使用广度或者深度有限搜索，在此图中找到一条增广路径的时间是$O(V+E_{f})=O(E)$,(注意到$2E > E_{f} > E > V - 1$),因而总时间为$O(E|f|)$，适用于流较小的情况

Edmonds-Karp算法

1. 对增广路径的选择不再任意，而是选择一条从源结点s到汇点t的最短路径，这可以通过广度优先搜索来实现
2. 时间为
3. $O(V^2E)$,其中找最短路径$O(E)$，流递增操作共执行 $O(VE)$次

最大二分匹配

1. 匹配： 给定一个无向图$G = (V,E)$，一个匹配是边的一个子集$M\subseteq E$,使得对于所有的结点$v \in V$，子集$M$中最多有一条边与之相连。
2. 最大匹配即含有最多边的匹配
3. 二分图： 即结点集合可以划分成$V = L\bigcup R$,其中L和R不相交，并且边集合中所有边都横跨L和R。进一步假定集合中的每个结点都至少有一条边（方便转化成最大流问题）
4. 实际应用，将L看成是机器集合，R是任务集合，E中有边(u,v)则表示机器u能够处理任务v。最大匹配能够让尽可能多的机器运转起来
5. 寻找最大二分匹配的做法就是将二分图$G = (V,E)$转化成流网络$G’ = (V’,E’)$，具体做法就是将L看成源结点集合，R看成是汇点集合，因而首先加上一个超级源结点s和超级汇点t以及这两者对应的边，原图中所有无向边的方向都定义成从L指向R，最后给流网络中所有边都赋予单位容量
6. 引理26.9：给定二分图$G$和对应的流网络$G'$，若$G$中存在一个匹配$M$，则$G'$中存在一个整数值的流$f$使得$|M| = |f|$，反之亦成立。并且满足$f(u,v) \neq 0$的边都是M中的边
7. 完整性定理26.10： 如果容量函数c只能去整数值，则Ford-Fulkerson方法所生成的最大流f满足|f|是整数值的性质，而且对于所有的结点u和v，f(u,v)的值都是整数
8. 推论26.11 二分图G中的一个最大匹配的基数等于其对应的流网络$G'$中某一最大流f的值
9. 总结就是，两者完全等价：$M=\{ (u,v) : (u,v) \in E, f(u,v) \neq 0\}$,并且$|M| = |f|$

习题

to be continued

代码实现