@zqbinggong
2016-06-21T02:33:06.000000Z
字数 5301
阅读 1690
| 姓名 | 学号 | 班级 | 选题 | 论述 | 结论 | 总分 |
|---|---|---|---|---|---|---|
| 张强 | 2013301020039 | 彭桓武班 |
the Analysis of Realistic Projectile Motion
张强 2013301020039 the final exam
code
Abstract
In the final exam,I choose the subject about the realistic projectile motion, in which I will consider several problems involving the motion of the objects through the atmosphere,easpecilly the trajectory of the cannnon.
Key words
Euler methonds,projectile,air drag,isothermal,adiabatic,Vpython,easygui
Background
The Euler method is the numerical approach I choose to deal with motion of the realistic projectile objects.In the begin,we just consider the case of two dimention,and then I will study the more realistic situation where a cannon flies in the sky,with air resistance.And the effec of the astomsphere will be considered.There are two simple approximation to treat the atomosphere as an isothmal ideal gas or an adiabatic ideal gas.
1.Projectile motion
1.Kinematic quantities of projectile motion
In projectile motion, the horizontal motion and the vertical motion are independent of each other; that is, neither motion affects the other. This is the principle of ''compound motion'' established by Galileo in 1638.Galileo Galilei, ''[[Two New Sciences]]'', Leiden, 1638, p.249
2.Acceleration
Since there is only in the vertical direction, the velocity in the horizontal direction is constant, being equal to  . The vertical motion of the projectile is the motion of a particle during its free fall. Here the acceleration is constant, being equal to g .The g is the Standard gravity|acceleration due to gravity. ( 9.81 m/s^2 near the surface of the Earth) The components of the acceleration are:
. The vertical motion of the projectile is the motion of a particle during its free fall. Here the acceleration is constant, being equal to g .The g is the Standard gravity|acceleration due to gravity. ( 9.81 m/s^2 near the surface of the Earth) The components of the acceleration are:


3.Velocity
The horizontal component of the [[velocity]] of the object remains unchanged throughout the motion. The downward vertical component of the velocity increases linearly, because the acceleration due to gravity is constant. The accelerations in the x and y directions can be integrated to solve for the components of velocity at any time t , as follows:
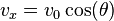

The magnitude of the velocity (under the Pythagorean theorem, also known as the triangle law):

4.Displacement
At any time t , the projectile's horizontal and vertical are:


The magnitude of the displacement is:

2.Air Drag
As is mentioned above and will be discussed thoroughly in our codes, air drag force plays a critical role in the shells' trajactory. But engineers have come up ideas of rifling to fight against such impedence.
Rifling is a series of spiral line inside the pipe of fire guns like rifles and cannons. When the shells get out of the pipe pushed by the gunpowder at the end of the bore of a gun, the high temperarure will inflate the shell making it rub with the rifling and spin. Such spin motion will effectively reduce the air drag force.
Air Density Distribution
In the first section we gave the form of air drag force under simple assumptions. Now we come to a stage a little more complex. The force is sill propotional to the density of air. However, the density of air is a decreaseing function of altitude.
Isothermal Condition
The simplest approximation is to treat the atmosphere as an isothermal ideal gas.One then finds that the pressure p depends on altitude according to
Adiabatic condition
The more realistic approach is to assume that the ait is a poor conductor of heat, and that convection is very slow.
The adiabatic approxination leads to a somewhat different dependence of the density on altitude
3.the implementation of the program
1.Firstly,the program ask you to input some parameters such as target coordinate,the effective attack range and the "h",which is used to determine the approximation methonds.For d=0,we consider the isothermal condition and d=1 for adiabatic condition.
2.Then,the program run ,calculate the firing speed and angular.
3.In the end, program draw the 2D with matplotlib or 3D trajectory using vpyhton according to the firing speed and angular calculated and outpute the related information.
Body
1. the case of two dimension


and the result are listed in figure1
| 目标水平距离 | 目标高度 | 有效打击半径 | 大气近似条件 | 发射角度 | 发射速度 |
|---|---|---|---|---|---|
| 20000 | 2000 | 10 | 等温近似 | 49.5 | 565.773929138 |
| 20000 | 2000 | 10 | 绝热近似 | 48.6 | 584.738975708 |
| 30000 | 3000 | 10 | 等温近似 | 49.8 | 733.751512241 |
| 30000 | 3000 | 10 | 绝热近似 | 48.6 | 779.306132074 |
According to the results,we draw a conclusion that the cannon needs faster speeds and smaller angular on adiabatic condition to hit the same target.
2.the 3D trajectory of the cannon


and the results are listed in the figure2
| 目标 | 目标 | 目标 | 有效打击半径 | 大气近似条件 | 发射角度 | 发射速度 |
|---|---|---|---|---|---|---|
| 10000 | 10000 | 10000 | 10 | 等温近似 | 37.3478897565 | 710.409868665 |
| 10000 | 10000 | 10000 | 10 | 绝热近似 | 36.7478897565 | 681.75948603 |
| 100000 | 1000 | 100000 | 100 | 等温近似 | 40.6478897565 | 1957.58009383 |
| 100000 | 1000 | 100000 | 100 | 绝热近似 | 40.6478897565 | 1957.58009383 |
According to the results,we find that when the target is far away from us,the initial speed ang angular calculated are the same.Besides,when the targer coordiante is set as(10000,10000,10000) where the Y-coordinate is the height of the target,we find that the result is different fron the case of two dimension
Show some details about easugui



Connclusion
The details of the conclusion are showed in the body,there I just want to say something about program and the similarity and difference between the case of 2D and 3D.
1.The program needs a long time to calculate the firing speed and angular,so you should be patient to wait the outcome information.
2.The 3D case is similar to the 2D case. In deed, we just rotate the firing plane around the y-axis by the angular of .

And
is the target coordinates.At this point,we should get the similar results about the relationship between the different approxiamtion approach used to deal with the effect of the atomsphere.This is problem as far as I can see.Unfortunately,I am at a lost what to do to deal with it.
Acknowledgement
1.Giodano, N.J., Nakanishi, H. Computational Physics. Tsinghua University Press, December 2007.
2.Wikipedia contributors. "Projectile motion." Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 5 Mar. 2016. Web. 2 Apr. 2016.
3.会编程的大白熊--Vpython
4. 使用matplotlib的示例:调整字体-设置刻度、坐标、colormap和colorbar等
5.Thanks to Liu Wentao for his template.
