基本算法和数据结构介绍

主要为《图解算法》的学习笔记和相关扩充

1 大O算法

1：O(运算次数)：表示运算最糟糕情况下 运算时间，表示算法时间的增速
python 中基本操作运行时间

2 数组链表

1. 在链表中添加元素很容易：只需将其放入内存，并将其地址存储到前一个元素中。必须先访问元素#1，从中获取元素#2的地址，再访问元素#2并从中获取元素#3的地址，以此类推，直到访问最后一个元素。需要同时读取所有元素时，链表的效率很高：你读取第一个元素，根据其中的地址再读取第二个元素，以此类推。但如果你需要跳跃，链表的效率真的很低。插入元素很简单，只需修改它前面的那个元素指向的地址
   ex: 网站分页浏览
2. 数组中：你知道其中每个元素的地址，便于随机访问，用数组时，则必须将后面的元素都向后移
3. 元素的位置称为索引

---

3栈

插入的待办事项放在清单的最前面；读取待办事项时，你只读取
最上面的那个，并将其删除。因此这个待办事项清单只有两种操作：压入
（插入）和弹出（删除并读取）

1调用栈：储存多个函数的变量

所有函数调用都进入调用栈。

1. 调用函数1时候 计算机为其分配一块内存，储存变量和参数
2. 在调用另一个函数2时 再分配一块内存，放在栈顶上
3. 调用函数2 返回 栈顶内存块弹出
4. 调用2 时候 当前函数暂停并处于未完成状态。该函数的所有变量的值都还在内存中

2 递归调用栈

存储详尽的信息可能占用大量的内存。每个函数调
用都要占用一定的内存，如果栈很高，就意味着计算机存储了大量函数调用的信息。
1重新编写代码，转而使用循环。
2使用尾递归。这是一个高级递归主题。

4 欧几里得求解公约数

The Euclidean Algorithm for finding GCD(A,B) is as follows:

1. If A = 0 then GCD(A,B)=B, since the GCD(0,B)=B, and we can stop.
2. If B = 0 then GCD(A,B)=A, since the GCD(A,0)=A, and we can stop.
3. Write A in quotient remainder form (A = B⋅Q + R)
4. Find GCD(B,R) using the Euclidean Algorithm since GCD(A,B) = GCD(B,R)
5. prove
   

#A=Q*B+R  if A>B
def GCD(A,B):
    if A==0:
        gcd=B
    elif B==0:
        gcd=A
    else:
        return GCD(B,A%B)
    return gcd
print(GCD(27,123))

5 分治法 divide and conquer

找出简单的基线条件；
确定如何缩小问题的规模，使其符合基线条件。

###1 Sum:

def my_sum(arr):
    if len(arr)==0:
        return 0
    elif len(arr)==1:
        return arr[0]
    else:
        t=arr.pop(0)  ### 如果不引入变量t  将 再删除一次
        return t+sum(arr)
list3=[4,5,3]
print(my_sum(list3))
##借鉴
def sum(list):
  if list == []:
    return 0
  return list[0] + sum(list[1:])

2 快速排序 quiksort

(1) 选择基准值。
(2) 将数组分成两个子数组：小于基准值的元素和大于基准值的元素。
(3) 对这两个子数组进行快速排序。

def quicksort(array):
  if len(array) < 2:
    # base case, arrays with 0 or 1 element are already "sorted"
    return array
  else:
    # recursive case
    pivot = array[0]
    # sub-array of all the elements less than the pivot
    less = [i for i in array[1:] if i <= pivot]
    # sub-array of all the elements greater than the pivot
    greater = [i for i in array[1:] if i > pivot]
    return quicksort(less) + [pivot] + quicksort(greater)
    ##
    def quick_sort(arr):
    if len(arr) <2:
    #基准
        return arr
    else:
        list1=[]
        list2=[]
        for i in arr[1:]:##c从序列1开始 递归 
            if i >= arr[0]:
                list1.append(i)
            else:
                list2.append(i)
    return quick_sort(list2)+[arr[0]] +quick_sort(list1)

3 最大子数组问题

股票的买卖 获得最大化的收益

1 暴力求解法

尝试对每种情况组合进行计算比较 共有$C(n,2)=\Theta(n^{2})$种情况
处理每种情况的时间至少是常量，运行时间$\Omega(n^{2})$

2分治法

考虑每日价格的变化
将问题转化为求解最大的非空连续子数组

1.利用前面求解的子数组和来计算当前子数组的和，使得每个子数组的计算时间为常数$O(1)$

2.分治策略求解

1 将数组划分为两个规模尽可能相等的两个子数组，找到数组的中央位置mid。
2 任意的连续子数组A【i，j】所处的位置必然是
2-1. 完全位于【low，mid】，low<=i<=j<=mid
2-2. 完全位于【mid，high】
2-3. 跨越中点mid i<=mid<=j
3 因为跨越中点的有限制 分别找出[i,mid] and [mid,j]的最大子数组
合并即可

3 代码实现

1 找到跨越中点的最大子数组
代码实现

子数组包含n个元素 则 运行时间为迭代次数n* 每次迭代时间 常数
$\Theta(1)$ 总时间为线性

2寻找总的最大
代码实现
* 分析运行时间：
* 对于基本情况 n=1 常量时间 $\Theta(1)$
* n>1: left and right are both n/2, each costs time :T(n/2)
* cross_mid $\Theta(n)$
* for compare part: T=$\Theta(1)$
*

$$T(n)=2T(n/2)+\Theta(n)$$
* 主方法求解 ： $$T(n)=\Theta(nlgn)$$

3 线性时间算法解决：动态规划 最后一个取不取

完整代码实现--暂留

比较模型 comparision sorting 最小O(nlgn)

1快速排序

1 最佳情况--最差情况

已经排好的列表 栈的长度每层都为O(n) 每层运行时间
如果取array【0】位参考值 一共需要n层 即栈的高度为O(n) 总时间O(n*n)----最差情况
而取 中间为基准 栈的高度为O(lgn) 总时间O(n*lgn)---最好

2 平均

每次参考值 随机选取
运行时间 O(nlgn)

2 Bubble sort 冒泡排序

阴影项正在比较它们是否乱序。如果在列表中有 n 个项目，则第一遍有 n-1 个项需要比较。重要的是要注意，一旦列表中的最大值是一个对的一部分，它将不断地被移动，直到遍历完成。

 swapped = false

for i = 1 to indexOfLastUnsortedElement-1



if leftElement > rightElement 

  swap(leftElement, rightElement)交换左右

  swapped = true

  while swapped

ef bubbleSort(alist):
    for passnum in range(len(alist)-1,0,-1):
        ###排序数目递减
        for i in range(passnum):
            if alist[i] > alist[i+1]:
                temp = alist[i]
                alist[i] = alist[i+1]
                alist[i+1] = temp ##交换位置

3 select sort

在每次遍历时，选择最大的剩余项，然后放置在其适当位置

repeat (numOfElements - 1) times
  set the first unsorted element as the minimum
  for each of the unsorted elements
    if element < currentMinimum
      set element as new minimum
    swap mininum with  first unsorted element

选择排序  
每次遍历 只交换一次
共n-1次遍历
O(N^2)
"""
def selectionSort(alist):
    for fillslot in range(len(alist)-1,0,-1):
        position_of_max = 0
        for location in range(1,fillslot+1):
            if alist[location] > alist[position_of_max]:
                ##确定最大值的位置
                position_of_max = location
        temp = alist[fillslot]
        ### 与最后的位置交换
        alist[fillslot] = alist[position_of_max]
        alist[position_of_max] = temp

4 insert sort

我们开始假设有一个项（位置 0 ）的列表已经被排序。在每次遍历时，对于每个项 1至 n-1，将针对已经排序的子列表中的项检查当前项。当我们回顾已经排序的子列表时，我们将那些更大的项移动到右边。 当我们到达较小的项或子列表的末尾时，可以插入当前项

mark first element as sorted
for each unsorted element X
  'extract' the element X
  for j = lastSortedIndex down to 0
    if current element j > X
      move sorted element to the right by 1
    break loop and insert X here

插入排序
n-1 次比较
O(n^2)
但是仅仅进行一次分配 
"""
def insertSort(alist):
    for index in range(1,len(alist)):
        ##遍历列表
        current = alist[index]
        position = index
        while position > 0 and alist[position-1] > current:
            ###向左移动比较   如果小  就移位  直到大
            alist[position] = alist[position - 1]
            position = position -1
        alist[position]= current

3 合并排序 merge sort

O(nlgn)

split each element into partitions of size 1
recursively merge adjancent partitions
  for i = leftPartIdx to rightPartIdx
    if leftPartHeadValue <= rightPartHeadValue
      copy leftPartHeadValue
    else: copy rightPartHeadValue
copy elements back to original array

4heapsort

O(nlgn)

5 search sort

O(n*n)

decision tree(graphical representation)

desicion tree ---> comparsion sort
利用决策树 证明 比较类算法排序 最低时间是$\Omega(nlgn)$
根据 决策树的叶子数进行证明： num>= n!,num <=$2^{n}$

linear time sort :(非比较模型)

1 couting sort :

stable sort : 相同元素排序后 与原排序顺序相同。
缺点： 1、取决于数字范围
2、 占用大量内存（c:初始化）

2 radix sort:

1 wrong sort： 高位先排序 排完第一位 分出一个箱子 拍各个小箱子里面的

2： IBM： 从低位开始排序 遵从 稳定排序： 在一个大箱子里面 多次遍历数组
？？？？ 后面的 分成字节 等内容 暂不理解
优点：处理的数据多，线性时间
缺点：快速排序占用内存大 ，所以不实用

6 基本数据结构

0 栈stack和队列queque

1. 栈： 后进先出 LIFO
2. queque： first in first put FIFO

1 stack

0.列表实现栈

完整代码 列表实现栈

class Stack:
    '''
    栈的操作 类
    '''
    def __init__(self):
        ###
        self.items = []
    def isEmpty(self):
        ###判断是否为空栈 返回布尔值
        return self.items == []
    def push(self,item):
        ## 压入 元素 添加到队尾
        self.items.append(item)
    def pop(self):
        ###从队尾删除
        return self.items.pop()
    def peek(self):
        ###返回栈顶部值
        return self.items[len(self.items)-1]
    def size(self):
        ###栈的大小
        return len(self.items)

1.INSERT 操作 称为压入 PUSH （S：表示一个数组容纳 n）

PUSH(S,x)
S.top=S.top+1
S[S.top]=x

2.DETLETE 操作 ：POP

POP(S)
if STACK-EMPTY(S)
    return error underflow
else:
    S.top=S.top-1
    return S[S.top+1]
    ###元素仍在数组里面 但是不再栈内

3.判断栈是否为空 如果空 空栈弹出 会underflow error

if S.top==0:
   return Turn
else:
   return False

运行时间：O(1)

两个stack transform a queue:
ENQUEUE pushes elements on B. DEQUEUE pops elements from A. If A is empty, the contents of B are transfered to A by popping them out of B and pushing them to A. That way they appear in reverse order and are popped in the original.
A DEQUEUE operation can perform in Θ(n) time, but that will happen only when A is empty. If many ENQUEUEs and DEQUEUEs are performed, the total time will be linear to the number of elements, not to the largest length of the queue.

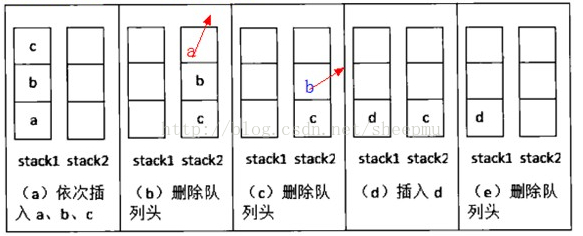
2栈 不为空就POP 为空 就把1栈的 pop insert进入 2

应用
1.利用栈 ：进行符号匹配检测---代码
2.利用栈 ： 十进制二（任意）进制转换---代码

---

2 queue

0

1.Queue() 创建一个空的新队列。 它不需要参数，并返回一个空队列。
2.enqueue(item) 将新项添加到队尾。它需要item作为参数，并不返回任何内容。
3.dequeue() 从队首移除项。它不需要参数并返回 item。 队列被修改。
4.isEmpty() 查看队列是否为空。它不需要参数，并返回布尔值。
5.size() 返回队列中的项数。它不需要参数，并返回一个整数。

完整代码实现

class Queue():
    """
    假定 队尾在列表的位置为0 
    删除队首 即是 列表的最后一个元素
    """
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return self.items == []
    def enqueue(self,item):
        self.items.insert(0,item)
        #### 列表0的位置插入  元素
    def dequeue(self):
        return self.items.pop()
    def size(self):
        return len(self.items)

利用数组Q[1...n]实现n-1个元素的队列 Q.head:指向队头元素 Q.tail: 指向下一个元素插入的位置
队列中元素在最后的位置形成环绕
Q.head=Q.tail+1 : full
Q.head=Q.tail : empty

1.INSERT : ENQUEUE(入队)

ENQUEUE(Q,x)：
if Q.head==Q.tail+1:
   return error :overflow
Q[Q.tail]=x
if Q.length==Q.tail:
    Q.tail=1   ###考虑 回环到队首情形
else:
    Q.tail+=1

2.DEQUEUE：delete

DEQUEUE(Q)

if q.head== nil:
    return underflow
x=Q[Q.head]
if Q.head==Q.length:
   Q.head=1
else:
   Q.head=Q.head+1

time:O(1）

Show how to implement a stack using two queues. Analyze the running time of the stack operations.

We have two queues and mark one of them as active. PUSH queues an element on the active queue. POP should dequeue all but one element of the active queue and queue them on the inactive. The roles of the queues are then reversed, and the final element left in the (now) inactive queue is returned.

The PUSH operation is Θ(1), but the POP operation is Θ(n) where n is the number of elements in the stack.

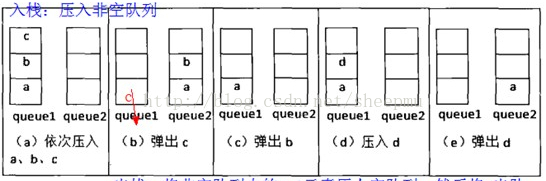
先把ab出q1并入q2,此时目标c跑到了队头，出q1。此时q1已经为空，下一个要出的是b,把a从q2出队并进q1,此时目标b在q2队头,出队........

约瑟夫问题

代码实现

---

3双端队列 deque：

插入删除均可以在两端进行

1 链表 linked list

各个对象按照线性顺序排列。顺序由各个对象里面的指针决定
单向链表 ----> 列表

完整实现代码
1.创建一个节点

class Node:
    """
    链表的基本 是 节点  
    每个节点 包含列表项本身   以及下一个 节点的引用
    """
    def __init__(self,initdata):
        self.data = initdata
        self.next = None
    def getData(self):
        return self.data
    def getNext(self):
        return self.next
    def setData(self,newdata):
        self.data = newdata
    def setNext(self,newnext):
        self.next = newnext

2.链表类本身不包含任何节点对象。它只包含对链接结构中第一个节点的单个引用

class UnorderedList:
    """
    每个节点通过显式引用链接到下一个节点
    第一个节点（包含第一个项）
    UnorderedList 类必须保持对第一个节点的引用
    """
    def __init__(self):
        self.head = None

3.添加一个节点

def add(self,item):
        temp = Node(item)## 创建一个新的结点
        temp.setNext(self.head)  ###新结点 连在旧的第一个
        self.head = temp  ### 头 引用 新的结点

4. remove一个节点

def remove(self,item):
        current = self.head 
        previous = None
        found = False
        while not found :   
            ### 搜索  假设 删除项存在
            if current.getData() == item :
                found = True
            else:
                previous =  current  ###pre 在 current 前一个节点
                current = current.getNext()
        if previous == None : ### 删除项 为列表第一项
            self.head = current.getNext()
        else:
            previous.setNext(current.getNext())

---

---

双向链表:每个对象 含有关键 key 和两个指针 next ，prev

1. x.prev=nil :没有前驱元素 链表第一个元素
2. x.next=nil:
3. x.head =nil 链表为空

1 链表的搜索

LIST-SEARCH(L,k) : 查找链表L中的第一个key：k 返回元素的指针

x=L.head
while x!=nil and x.key!=k:
      x=x.next
return x 
###Time : worst case : $\Theta(n)$

2 链表插入

元素x：key 插入到链表的前段

LIST-INSERT(L,x)
x.next=L.head  ### l.head 指向表头元素  新元素指向原来的表头元素
if L.head != NIL:
    L.head.prev=x
L.head =x
x.prev=NIL

3 链表的删除

1. 给定元素的指针 通过修改指针进行删除
2. 给定key值 需要先search 找到指针

LIST-DELETE(L,x)
if x.prev!=NIL:
   x.prev.next=x.next
else:
   L.head= x.next
 if x.next!=NIL:
    x.next.prev=x.prev
    ### Time: O(1)

4 哨兵 ：简化代码 暂留！！

10.2-5: 单向循环链 实现字典操作 ： search delete insert

10.2—6两个不相交的集合的交集

if both sets are a doubly linked lists, we just point link the last element of the first list to the first element in the second. If the implementation uses sentinels（哨兵）, we need to destroy one of them.

10.2-7 : n个元素的单行链逆转 Time: $\Theta(n)$ Space :固定大小的储存空间。
cpp solution
10.2-8: 仅使用一个指针实现双向链表 ，在O（1） 时间内实现逆转

2 指针和对象实现

1 对象的多数组表示

指针x为key，prev，next的共同下标
key16->key4 4 is key2,16 is key[5] so :next[5]=2,prev2=5
ps: NIL 出现在队尾的next 和队首的prev 通常用不代表数组实际位置的整数（-1） 表示
L储存表头元素的下标

2 对象的单数组表示

程序设计语言中 一个对象 在计算机内存里面占据一组连续的储存单元。指针只是该对象第一个存储单元的地址，访问该对象的其他元素 需要指针上添加偏移量

在没有显式的指针数据结构类型环境下：

图示为单数组A的储存图：
一个对象占据一段连续的子数组A[j,k] 对象中每个属性 对应一个偏移量
指向该对象的指针为下标j，读取i.prev=A[i+2]

单数组容易处理异构的数据

3 对象的分配和释放： 多数组的双向链表为例

1.数组长度为m 有n个对象储存 剩下 m-n个对象是自由
2. 自由对象保存在一个 单链表 ： free list
3. 自由表只储存next指针 头部保存在全局变量free中
4. 自由表类似于一个栈 ，pop和push 实现 对象的分配和释放。

ALLOCATE—OBJECT（）
if free==NIL:  ##假设free指向自由表的第一个元素
    error "out of range"
else:
    x=free
    free=x.next
    return x  ###返回可以插入key的下标

FREE_OBJECT(x)
x.next=free ## 对象的next 指向前一个free  因为是push
free=x  删除的对象自身 变成free 第一个

10.3-4 双向链表保持紧凑，占用前m个下标位置
ans：We can allocate elements in the beginning of the array. Whenever we deallocate an element, other than the last (in the stack), we need to shift all elements after it left and then update all the indices that point beyond the deleted element (by decrementing them). This will take linear time. As an optimization, whenever we deallocate the last element in the array, we don't need to scan the array and update pointers.
每次 删除后调整 key值位置

3 有根树 的表示：

树的结点用对象表示，每个结点有关键字key 还有指向其他结点的指针

1 二叉树

p,left,right 分别指向父结点 左孩子 右孩子
1. x.p=NIL x is root
2. T.root-> 指向整个树的根结点 T.root=NIL empty

2 分支无限的有根树

1. left and right replace with child1 child2 。。。。
2. 结点数无限制时候 不知预先分配多少属性 而且 多数结点只有少量的child，浪费储存空间

左孩子 右兄弟表示法
1.x.left.child 指向 x**最**左边的孩子结点
2.x.right.sibling 指向 右侧相邻的兄弟结点

7 散列表hashtable ：将输入映射到数字索引位置

python中的字典
支持 INSERT DELET SEARCH操作

0要求

1. 它应将不同的输入映射到不同的数字
2. 每次结果必须是一致

0基本思想

散列函数将不同的输入映射到不同的索引。avocado映射到索引4，milk映射到索引0。每种商品都映射到数组的不同位置，让你能够将其价格存储到这里。

1 直接寻址表

关键字的全域比较小

缺点： 关键字集合相对U很小 分配给T的空间浪费

2 散列表

直接寻址：关键字k的元素储存在 槽k中
散列方式： 储存在 h(k)中 利用散列函数 计算出槽的位置

1 冲突

1 链接法解决冲突

散列到同一个槽中的元素放到一个链表中 ：双链表 更快删除一个元素 可以在O（1）时间内删除

1 填装因子：散列表包含元素/位置总数

存放n个元素的 具有m个槽的散列表T load factor ：n/m

一旦填装因子大于0.7，就调整散列表的长度。
你可能在想，调整散列表长度的工作需要很长时间！你说得没错，调整长度的开销很大，因
此你不会希望频繁地这样做。但平均而言，即便考虑到调整长度所需的时间，散列表操作所需的
时间也为O(1)

2

1. 最坏的性能 n个关键字 散列到同一个槽 $\Theta(n)$

2. 平均性能： 取决于 散列函数 散列到槽位上的均匀程度

3 简单均匀散射

任何一个给定的元素等可能的散列到m个槽中 任何一个，且与其他元素的散列位置无关

1.简单均匀散射，用链接法解决冲突的散射表，一次不成功的查找平均时间为\Theta(1+a)
2.简单均匀散射，一次成功的查找时间为\Theta(1+a)

如果散列表中的槽数与表中元素 n=O(m)，字典的所有操作的平均水时间 均为O（1）

3 散列函数

1. 将关键字转化为自然数

1 除法散列法

$$h(k)=k mod m$$ 关键字
避免m选择某些值 m应一个 不太接近2 的整数幂的素数
reason：
1.$m=2^{r}$ 二进制数k 对其取余 得到的结果就是二进制后r位 所以h(k)的取值与高位无关
2.keys 均为 偶数 取余结果只有偶数 奇数槽没有利用到

2 乘法散列

1.

$$h(k)=[m(kA mod 1 )]$$
ps: KA mod 1 取kA的小数部分 最后向下取整

1. assum: $m=2^{r}$ k: a w-bit word
   $$h(k)=(A*k mod 2^{w}) rsh (w-r)$$
   ps: $2^{W}<A<2^{w}$ rsh: 二进制向右移

Example:
$clot:m=2^{3}$, w=7 bit , A=1011001

1.for k * A =2w bit mod $2^{w}$
-->get w bit
2.right shift (w-r)
-->get r bit

3 全域散列： 随机的选择散列函数

1 Define: 全域（universal）： 一组有限散射列函数，将给定的关键字全域U映射到{0,1,2,...,m-1}之中，这样的一个函数组成为全域的。

全域关键字 k,l for k!=l and h(k)=h(l) 发生的概率不大于1/m
这样的函数 h～H 最多有 |H|/m

2 run time (expected)

m个槽位的表，全域散射和；链表法解决冲突，需要\Theta(n)的时间处理
O（m）个 INSERT 操作 a=O(1) 所以n个操作序列的期望时间为O（n)

3 Consrtucting a universal hash functions

1. m is prime 类似于 m进制 将k分解成(r+1) 位
   $k={k0,k1,k2,k3,....k_{r}},0<k_{r}<m$ ##对m不停取余

2. pick a from $<a_{0},a_{1},.....a_{i}>$
   each $a_{i}$ is chosen randomly from {0,1,2...n-1}
   each $a_{i}$ ---> hash function

3. Define $h_{a}(k)=(\sum_{i=0}^{r}a_{i}k_{i})$ mod m

4. The size of the set function :
   $|H|= m^{r+1}$ ##每一位有 m的取值可能 共r+1位

5. prove H is universal
   (暂略 详见笔记本)

4 开放寻址法 （open addressing）

1.每个表项 或者包含动态集合的一个元素 或者包含NIL。查找元素时候 系统查找所有表项 直到找到 或者不在表内。
2. 开放寻址法不需要 指针，节省储存指针的空间，

HASH-INSERT(T,K)
i=0
while i< m:
     j=h(k,i)
     if T[j]== NIL:
         T[j]=k
         return j  ##f 返回k的储存槽位
         break
     else:
         i=i+1
     if i==m:
        error "hash table overflow"

HASH-SEARCH(T,K)
i=0
while i< m:
   j=h(k,j)
   if T[j]==k:
      return j 
      break
    i=i+1
    if i== m or T[j]=NIL:
        return NIL

hashtable is difficult for deletion
删除槽i中的值 如果以NIL标记 槽i后面的关键子检索 不到
solution: 槽i中放置一个特定 的DELETE 值 搜索的时候跳过DELETE标示

1 探查序列

1.均匀散列 uniform hashing
define: 每个关键字的探查序列等可能的为<0,1,2,3....m-1>的m! 排列的一种

1 线性探查

给定一个辅助散列函数 h'
$h(k,i)=(h'(k)+i) mod m ; i=0,1,2,...m-1$
for k search T[h'(k)] first , next T[h'(k)+1] until T[m-1]
and then T[0],T1....

It's easy to implement
Problem: 一次群集（primary clustering）：连续被占用的槽很多
一个空槽前面有i个满的槽时候，该槽为下一个占用的概率是（i+1）/m

2 二次探查 (quadratic probing)

$h(k,i)=(h'(k)+ c_{1}i + c_{2}i^{2} mod m;i=0,1,2,3...m-1$
偏移量以二次的方式依赖与 探测序号i
Problem: 初始探测位置相同 探测序列相同 h(k1,0)=h(k2,0)---->h(k1,i)=h(k2,i)

3 双重散列 (double hashing)

$$h(k,i)=(h1(k)+ih2(k)) mod m$$
Ps: 初始探测位置为 T[h1(k)],后续的探测位置为 偏移量的模
h2(k) 必须要与表m互质
1. m 取值2 的幂指数，h2 产生奇数
2. m取素数 好h2 产生比m小的素数 $$h_{2}(k)=1+(k mod m');m'=m-1$$

双重散列 用到了$\Theta(m^{2})$种探查序列

2.开放寻址法的分析

Assumption :uniform hashing

1. 均匀散列，一次不成功 的查找 即找到空槽至多为 1/(1-a)
   Proof :

   1. 1st probe : collision $n/m$
   2. 2nd probr : collision $n-1/m-1$
   3. $$E=1+n/m(1+(n-1)/(m-1)(1+(n-2)/(m-2)....(1+1/m-n))))<= 1/1-\alpha$$

2. 平均情况 插入一个元素至少要 1/（1-a)次探查

3. 成功探查的期望次数

   $$\frac{1}{\alpha}ln\frac{1}{1-\alpha}$$

5 完全散列 (perfect hashing)

1. Two level scheme , and each is universal hashing
   

2. 发生碰撞 key 放入另一个hashtable

3. level-2 : n keys(collision)----.> $n^{2}$ slots
   So we can prove that:
   

   $$E(collision)<\frac{1}{2}$$
   PS: 平均碰撞次数小于半次 即 没有碰撞(证明详见笔记本)

4. 完全散列的储存空间总量 保持O（n)

5. 应用： 安全散列算法（secure hash algorithm）

SHA是一个散列函数，它生成一个散列值——一个较短的字符串。
用于创建散列表的散列函数根据字符串生成数组索引，而SHA根据字符串生成另一个字符串。对于每个不同的字符串，SHA生成的散列值都不同

例：储存密码

当前，最安全的密码散列函数是bcrypt

4 应用

1. 散列表被用于大海捞针式的查找。例如，你在访问像http://adit.io这的网站时，计算机必须将adit.io转换为IP地址这个过程被称为DNS解析
   （DNS resolution），散列表是提供这种功能的方式之一。
   
2. 缓存是一种常用的加速方式，所有大型网站都使用缓存，而缓存的数据则存储在散列表中！
   (1) 你向Facebook的服务器发出请求。
   (2) 服务器做些处理，生成一个网页并将其发送给你。
   (3) 你获得一个网页。
   Facebook不仅缓存主页，还缓存About页面、Contact页面、Terms and Conditions页面等众多其他的页面。因此，它需要将页面URL映射到页面数据。

1

B.将字符串的长度用作索引。
C. 将字符串的第一个字符用作索引。即将所有以a打头的字符串都映射到散列表的同一个位置，以此类推。
D. 将每个字符都映射到一个素数：a = 2，b = 3，c = 5，d = 7，e = 11，等等。对于给定的字符串，这个散列函数将其中每个字符对应的素数相加，再计算结果除以散列表长度的余数。
例如，如果散列表的长度为10，字符串为bag，则索引为(3 + 2 + 17) % 10 = 22 % 10 = 2。

7 广度优先搜索

1. 使用图来建立模型（图由节点和边组成）
2. 使用广度优先搜索 解决问题

1广度优先搜索：
在广度优先搜索的执行过程中，搜索范围从起点开始逐渐向外延伸，即先检查一度关系，再检查
二度关系

2你需要按添加顺序进行检查。有一个可实现这种目的的数据
结构，那就是队列（queue）

3用代码实现图
节点和节点间联系可以用散列表实现
散列表无序 添加顺序不影响

graph['liu']=['zou','xiao','wei']
graph['zou']=['li']

在Python中，可使用函数deque来创建一个双端队列。

4添加一个查找过人的列表，避免重复和死循环

5运行时间
如果你在你的整个人际关系网中搜索芒果销售商，就意味着你将沿每条边前行（记住，边是从一个人到另一个人的箭头或连接），因此运行时间至少为O(边数)。你还使用了一个队列，其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的，即为O(1)，因此对每个人都这样做需要的总时间为O(人数)。所以，广度优先搜索的运行时间为O(人数 + 边数)，这通常写作O(V+E)，其中V为顶点（vertice）数，E为边数。

5图结构 --树
这种图被称为树。树是一种特殊的图，其中没有往后指的边
例如 家族谱

8 狄克斯特拉算法 解决加权图

带权重的图称为加权图（weighted graph）

1. 图中 可能存在环 最短路径 要绕开 环（无向图为 一个环）
2. 沿父节点回溯， 确定最短路线
3. 如果有负加权，无法解决：这是因为狄克斯特拉算法这样假设：对于处理过的海报节点，没有前往该节点的更短路径。
   这种假设仅在没有负权边时才成立

4 代码实现：
1个散列表 记录所有的图 各个节点及其邻居
1个散列表 记录各个节点的消耗
1个散列表 记录父节点
1个列表 记录已经标注过的节点

# the graph
graph = {}
graph["start"] = {}
graph["start"]["a"] = 6
graph["start"]["b"] = 2
graph["a"] = {}
graph["a"]["fin"] = 1
graph["b"] = {}
graph["b"]["a"] = 3
graph["b"]["fin"] = 5
graph["fin"] = {}
# the costs table
infinity = float("inf")
costs = {}
costs["a"] = 6
costs["b"] = 2
costs["fin"] = infinity
# the parents table
parents = {}
parents["a"] = "start"
parents["b"] = "start"
parents["fin"] = None
procceded=[]    ### 标记过的节点
def find_lowest_cost_node(costs):  ###找到最近的节点
    lowest_cost=float("inf")  ##无穷  节点消耗
    lowest_cost_node=None   ###节点
    for n in costs:          
        cost=costs[n]
        if cost < lowest_cost and n not in procceded:
            lowest_cost=cost
            lowest_cost_node=n
    return lowest_cost_node
node=find_lowest_cost_node(costs)
while node is not None:  ###遍寻所有节点
    cost=costs[node]  ###节点消耗
    neighbors=graph[node]  ###节点邻居
    for n in neighbors.keys():  ###节点邻居消耗更新
        new_cost=cost+neighbors[n]   
        if new_cost < costs[n] :
            costs[n]=new_cost
            parents[n]=node    ###更新父节点
    procceded.append(node)  ### 去除节点
    node=find_lowest_cost_node(costs)
print(costs)
print(cost)
print(parents)

(1) 找出最便宜的节点，即可在最短时间内前往的节点。
(2) 对于该节点的邻居，检查是否有前往它们的更短路径，如果有，就更新其开销。
(3) 重复这个过程，直到对图中的每个节点都这样做了。
(4) 计算最终路径。（父节点）

9 Bellman-Ford algorithm: 解决负加权时候的最短路径算法（留）

10 贪婪算法

每步都选择局部最优解，最终得到的就是全局最优解
并非所有情况都能得到完美解 有时候是近似最优解

1 集合覆盖问题

(1) 选出这样一个广播台，即它覆盖了最多的未覆盖州。即便这个广播台覆盖了一些已覆盖
的州，也没有关系。
(2) 重复第一步，直到覆盖了所有的州。
运行速度约为 O(n^2)

#需要的数字集合
number_needed=set([3,5,6,7,8])
#字母包含的数字
graph={}
graph['A']=set([1,2,3,4])
graph['B']=set([2,3,5])
graph['C']=set([3,5,6])
graph['D']=set([3,7,8,2])
#需要最少的字母列表
char_selection=[]
#循环 直到 需要的字母集合为空
while number_needed :
    best_char=None
    ##字母包含的数字和需要数字的集合
    number_covered=set()  
    for  char, num in graph.items():
        covered=num & number_needed
        if len(covered) > len(number_covered):
            number_covered=covered
            best_char=char
    ##添加 重合最多的字母
    char_selection.append(best_char)
    ###从待需要集合 减去 选出的数字
    number_needed=number_needed-number_covered
print(char_selection)

2判断是否为NP问题

non-deterministic polynomial
非确定性多项式时间复杂性类，包含了可以在多项式时间内，对一个判定性算法问题的实例，一个给定的解是否正确的算法问题。

1元素较少时算法的运行速度非常快，但随着元素数量的增加，速度会变得非常慢。
2涉及“所有组合”的问题通常是NP完全问题。
3不能将问题分成小问题，必须考虑各种可能的情况。这可能是NP完全问题。
4如果问题涉及序列（如旅行商问题中的城市序列）且难以解决，它可能就是NP完全问题。
5如果问题涉及集合（如广播台集合）且难以解决，它可能就是NP完全问题。
6如果问题可转换为集合覆盖问题或旅行商问题，那它肯定是NP完全问题

11 动态规划 ：子问题-大问题

1 背包问题

1 装物品 金额最大

1.余下了空间时，你可根据这些子问题的答案来确定余下的空间可装入哪些商品
2.各行的排列顺序无关紧要。

3.假设你在杂货店行窃，可偷成袋的扁豆和大米，但如果整袋装不下，可打开包装，再将背包倒满。在这种情况下，不再是要么偷要么不偷，而是可偷商品的一部分。如何使用动态规划来处理这种情形呢？
答案是没法处理。使用动态规划时，要么考虑拿走整件商品，要么考虑不拿，而没法判断该不该拿走商品的一部分。但使用贪婪算法可轻松地处理这种情况！首先，尽可能多地拿价值最高的商品；如果拿光了，再尽可能多地拿价值次高的商品，以此类推。

4
处理相互依赖的情况
例如：将埃菲尔铁塔加入“背包”后，卢浮宫将更“便宜”：只要1天时间，而不是1.5天
无法处理

5
但根据动态规划算法的设计，最多只需合并两个子背包，即根本不会涉及两个以上的子背包。不过这些子背包可能又包含子背包。

2 公共字母

1 最长 公共 子串

2 最长公共子序列

伪代码

if word_a[i]==word_b[j]:
    cell[i][j]=cell[i-1][j-1]+1  ##左上角 加一
else:
    cell[i][j]=max(cell[i-1][j],cell[i][j-1])  ##左面 或者上面最大

3应用

1.生物学家根据最长公共序列来确定DNA链的相似性，进而判断度两种动物或疾病有多相似。最长公共序列还被用来寻找多发性硬化症治疗方案。
2.你使用过诸如gitdiff等命令吗？它们指出两个文件的差异，也是使用动态规划实现的。
3.前面讨论了字符串的相似程度。编辑距离（levenshteindistance）指出了两个字符串的相似程度，也是使用动态规划计算得到的。编辑距离算法的用途很多，从拼写检查到判断用户上传的资料是否是盗版，都在其中。
4.你使用过诸如MicrosoftWord等具有断字功能的应用程序吗？它们如何确定在什么地方断字以确保行长一致呢？使用动态规划！

12 K最近邻算法（k-nearest neighbours）---机器学习

1 创建 推荐系统

1. 抽取 特征---计算距离（余弦相似度）留！！
2. 回归---预测结果 寻找紧邻 平均值

2 OCR 光学字符识别optical character recognition

(1) 浏览大量的数字图像，将这些数字的特征提取出来。
(2) 遇到新图像时，你提取该图像的特征，再找出它最近的邻居都是谁

3 创建垃圾邮件过滤器--朴素贝叶斯分类器（留）计算概率

13 树

0 定义

1. 层数：节点 n 的层数为从根结点到该结点所经过的分支数目。 根节点的层数为零。
2. 高度：树的高度等于树中任何节点的最大层数

1 列表表示树

完整代码实现

Mytree=['a', ##root
        ['b',  ##  leftchild  left_subtree
         ['d',[],[]],
         ['e',[],[]]],
        ['c', ### 1st rightchild righr sub-tree
         ['f',[],[]]]
        ]
####Mytree[0]: root   Mytree[1] leftsubtree  Mytree[2]: right_subtree      

def BinaryTree(r):
    ###构造一个具有根结点和两个子列表为空
    return [r,[],[]]

def InsertLeftBranch(root,newBranch):
    ###添加左子树 
    t = root.pop(1)
    if len(t) > 1:
        ##左child有值
        root.insert(1,[newBranch,t,[]])
    else:
        root.insert(1,[newBranch,[],[]])

def GetRootValue(root):
    ### 获取根结点值
    return root[0]

def SetRootValue(root,newVal):
    root[0]=newVal

def GetLeftChild(root):
    ### get the left subtree
    return root[1]

2 用结点 表示 树

完整代码实现

1 二叉搜索树（binary search tree）

1 define：

每个结点就是一个对象，除了key 和卫星数据外，包含上属性：left right parent .对于其中的每个节点，左子节点的值都比它小，而右子节点的值都比它大。

2 中序遍历 ：递归算法 输出所有的key

INORDER-TREE-WALK(x)
if x!= NIL:
    INORDER-TREE-WALK(x.left)
    print(x.key)
    INORDER-TREE-WALK(x.right)

运行时间

2 （B树，红黑树，堆，伸展树）。

14 反向索引

1 搜索 引擎

一个散列表，将单词映射到包含它的页面
搜索引擎发现页面A和B包含hi，因此将这些页面作为搜索结果呈现给用户

15 并行算法

1

那就是速度的提升并非线性的，因此即便你的笔记本电脑装备了两个而不是一个内核，算法的速度也不可能提高一倍

1. 并行性管理开销。假设你要对一个包含1000个元素的数组进行排序，如何在两个内核之间分配这项任务呢？如果让每个内核对其中500个元素进行排序，再将两个排好序的数组合并成一个有序数组，那么合并也是需要时间的
2. 负载均衡。假设你需要完成10个任务，因此你给每个内核都分配5个任务。但分配给内核A的任务都很容易，10秒钟就完成了，而分配给内核B的任务都很难，1分钟才完成。这意味着有那么50秒，内核B在忙死忙活，而内核A却闲得很！你如何均匀地分配工作，让两个内核都一样忙呢？

2是分布式算法-Mapreduce

开源工具Apache Hadoop
分布式算法非常适合用于在短时间内完成海量工作，其中的MapReduce基于两个简单的理念：映射（map）函数和归并（reduce）函数.

1 映射

映射是将一个数组转换为另一个数组
map()传入的第一个参数是f，即函数对象本身。由于结果r是一个Iterator，Iterator是惰性序列，因此通过list()函数让它把整个序列都计算出来并返回一个list。

def f(x):
    return x*x
r=list(
map(f,[1,2,3,4,5,6,7]))
print(r)

2reduce

而归并是将一个数组转换为一个元素
再看reduce的用法。reduce把一个函数作用在一个序列[x1, x2, x3, ...]上，这个函数必须接收两个参数，reduce把结果继续和序列的下一个元素做累积计算，其效果就是：

reduce(f, [x1, x2, x3, x4]) = f(f(f(x1, x2), x3), x4)

2 归并

归并是将一个数组转换为一个元素

16 布隆过滤器和 HyperLogLog

1 布隆过滤器 ---概率数据结构

2HyperLogLog

如果Google要计算用户执行的不同搜索的数量，或者Amazon要计算当天用户浏览的不同商品的数量，要回答这些问题，需要耗用大量的空间！对Google来说，必须有一个日志，其中包含用户执行的不同搜索。有用户执行搜索时，Google必须判断该搜索是否包含在日志中：如果答案是否定的，就必须将其加入到日志中。即便只记录一天的搜索，这种日志也大得不得了。

17 局部敏感的散列算法---Simhash

SHA算法：如果你修改其中的一个字符，再计算其散列值，结果将截然不同！局部不敏感
Simash：如果你对字符串做细微的修改，Simhash生成的散列值也只存在细微的差别
Simash 用来检查相似：
1.Google使用Simhash来判断网页是否已搜集。 2.老师可以使用Simhash来判断学生的论文是否是从网上抄的。
3.cribd允许用户上传文档或图书，以便与人分享，但不希望用户上传有版权的内容！这个网站可使用Simhash来检查上传的内容是否与小说《哈利·波特》类似，如果类似，就自动拒绝。

18 线性规划-----Simplex：解决最优化