CF733F Drivers Dissatisfaction 题解

题解 算法 杂题

题目大意：

给定一个 $N$ 个点 $M$ 条边的无向图，保证图联通。每条边有两个属性 $w_i$ 和 $c_i$ ，表示使这条边的权值每降低 $1$ 要花费 $c_i$ 的花费。现在你有一个总费用 $S$ ,你可以降低某些边的权值(可以降为负数，且总费用不得超过 $S$ ) 。问降低权值后，这张图可得到的最小生成树权值是多少，并且输出选为最小生成树中的边的编号及权值。

解析

首先明确一点：题目中说可以降低某些边的权值，其实如果我们只选 $c_i$ 最小的那条边，并只降低它的权值，这样一定可以使权值降低的最多（一点贪心的思想）。

我们可以首先找出这张图的最小生成树，并将在树上的边标记。然后，我们考虑降低哪条边的权值。

1. 如果降低树边的权值

   其实非常好做。由开头所讲，只需要找到树边中 $c_i$ 最小的那条边，将其 $w_i$ 减少 $\frac {S}{c_{min}}$ 即可。

2. 如果降低非树边的权值

   这种情况稍微有些麻烦，我们来看下面这张图：

   

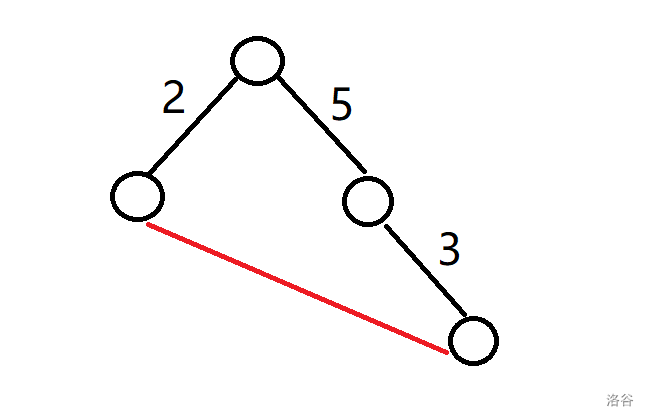
   黑色的边表示树边，而红色的这条边表示我们选择的要降低权值的这条边。

   由树的性质，我们不难发现：给树上两点间加上一条边后，便会生成一个环，由加上的边与两点间简单路径组成。要想其重新变回一棵树，那么必须从两点间的简单路径上去删除一条边。由贪心的思想，我们知道，要是最后答案最小，那么删去的边一定是两点间简单路径上权值最大的边。

   于是，我们可以枚举每一条非树边，找到其连接的两点的树上简单路径上权值最大的边，计算备选答案。

   备选答案就是 $sum-w_{max}+w_i-\frac{S}{c_i}$ ，其中 $sum$ 表示原图最小生成树的权值和。

   对于找两点间权值最大的边，我们可以请出我们的树链剖分。码量虽然大，但是很好理解呀!

最后对于路径的输出(真恶心) , 把要选的边标记即可。有很多小细节，在代码里有呈现。本人蒟蒻，不喜勿喷！

#include<iostream>
#include<algorithm>
using namespace std;
#define int long long
const int N=2e5+5;
int n,m,S;
int w[N],rec[N];
int sum,rev;
int he[N],ne[N<<1],go[N<<1],tot;
int fa[N];
struct node{
    int u,v,we,c,id;
    bool operator <(const node W) const{
        return we<W.we;
    }
}a[N];
bool st[N];
inline void add(int a,int b){
    ne[++tot]=he[a];he[a]=tot;go[tot]=b;
}
inline int find(int x){
    if(x!=fa[x]) return fa[x]=find(fa[x]);
    else return x;
}
inline void kruskal(){//最小生成树模板
    int cnt=0;
    sort(a+1,a+m+1); 
    for(int i=1;i<=m;i++){
        int A=find(a[i].u),B=find(a[i].v);
        if(A!=B){
            fa[B]=A;
            add(a[i].u,a[i].v);
            add(a[i].v,a[i].u);
            //建树
            cnt++;st[i]=1;sum+=a[i].we;
            //st[i]=1表示第i条边是一条树边
            //sum存储最小生成树的权值和
        }
        if(cnt==n-1) break;
    }
}
int top[N],dep[N],f[N],son[N],si[N];
int dfn[N],nw[N],cnt;
inline void dfs1(int u,int p){
    f[u]=p;dep[u]=dep[p]+1;
    si[u]=1;
    for(int i=he[u];i;i=ne[i]){
        int v=go[i];
        if(v==p) continue;
        dfs1(v,u);
        si[u]+=si[v];
        if(si[son[u]]<si[v]) son[u]=v;
    }
}
inline void dfs2(int u,int tp){
    top[u]=tp;
    dfn[u]=++cnt;
    nw[cnt]=w[u];
    if(son[u]) dfs2(son[u],tp);
    else return ;
    for(int i=he[u];i;i=ne[i]){
        int v=go[i];
        if(v==f[u]||v==son[u])continue;
        dfs2(v,v);
    }
}
struct Seg_Tree{
    int l,r;
    int val;
    #define lson (p<<1)
    #define rson (p<<1|1)
}t[N<<2];
inline void build(int p,int l,int r){
    t[p].l=l;t[p].r=r;
    if(l==r){
        t[p].val=nw[l];
        return ;
    }
    int mid=l+r>>1;
    build(lson,l,mid);
    build(rson,mid+1,r);
    t[p].val=max(t[lson].val,t[rson].val);
}
inline int query(int p,int l,int r){
    if(t[p].l>=l&&t[p].r<=r)return t[p].val;
    int res=0;  
    if(t[lson].r>=l) res=max(res,query(lson,l,r));
    if(t[rson].l<=r) res=max(res,query(rson,l,r));
    return res; 
} 
inline int query_max(int x,int y){
    int res=0;
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]])
            swap(x,y);
        res=max(res,query(1,dfn[top[x]],dfn[x]));
        x=f[top[x]];
    }
    if(dep[x]>dep[y]) swap(x,y);
    res=max(res,query(1,dfn[son[x]],dfn[y]));
    //边权转点权，最后一部分的上点应取 son[x]
    return res;
}
//---------------以上均为模板---------------//
signed main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) fa[i]=i;
    for(int i=1;i<=m;i++) cin>>a[i].we,a[i].id=i; //由于要输出边的序号，将其存进结构体
    for(int i=1;i<=m;i++) cin>>a[i].c;
    for(int i=1;i<=m;i++)
        cin>>a[i].u>>a[i].v;
    cin>>S;
    kruskal(); //最小生成树，同时建树
    rev=sum; //选非树边时方便得到备选答案，将最小生成树的权值拷贝一份
    dfs1(1,0);
    //由于题中给的是边权，我们可以将边权化为点权，用边连接的两点中深度更大的那个点的权值作为这条边的权值。
    for(int i=1;i<=m;i++){
        if(!st[i]) continue; //只处理树边
        if(dep[a[i].u]>dep[a[i].v]) w[a[i].u]=a[i].we,rec[a[i].u]=i;
        else w[a[i].v]=a[i].we,rec[a[i].v]=i;
        //w记录树中点权。rec表示该点向上连接的边的编号，输出时要用
    }
    dfs2(1,1);
    build(1,1,n);
    int minn=0x3f3f3f3f,id=0;
    //首先处理树边
    for(int i=1;i<=m;i++)
        if(st[i]){
            if(a[i].c<minn){
                minn=a[i].c;
                id=i;
                //minn找到树边中c[i]的最小值，id记录该边的编号
            }
        }
    int r=S/minn;
    sum-=r;//备选答案之一：选择树边
    bool flag=1; //由于两种情况在输出路径时的处理方式不同，因此记录改用哪种处理方式。
    int rd=0,cut=0;
    //如果选择了某条非树边比选择树边更优
    //那么flag标记为0,cut记录选择的那条边的权值，rd记录那条边的编号
    //蒟蒻想不出更多变量名了呜呜呜
    for(int i=1;i<=m;i++)
        if(!st[i]){
            int res=query_max(a[i].u,a[i].v);
            //找到两点简单路径中边权最大的边
            int r=S/a[i].c;
            if(rev-res+a[i].we-r<sum){ //解析中公式有呈现
                sum=rev-res+a[i].we-r;
                flag=0;rd=i;cut=res;
                //备选答案之二：选择非树边
            }
        }
    cout<<sum<<endl;
    if(!flag){ //如果选非树边更优
        int x=a[rd].u,y=a[rd].v;
        //由于query_max只能找到最大的数值而不能找到到底是那条边，因此枚举简单路径上的边即可
        while(1){
            if(dep[x]<dep[y]) swap(x,y);
            if(w[x]==cut) { //如果当前边边权为要删去的边的边权
                st[rec[x]]=0; //rec在这里派上用场:边权化为点权，x向上连接的那条边即为要删去的边
                st[rd]=1; //这条非树边标记
                int r=S/a[rd].c;
                a[rd].we-=r;
                break;
            }
            x=f[x]; //树剖的f和并查集的fa别搞混了(掉了几次坑的蒟蒻如是说)
            //每次向上跳一个
        }
        for(int i=1;i<=m;i++)
            if(st[i])
                cout<<a[i].id<<" "<<a[i].we<<endl; //sort会打乱边的顺序，因此输出a[i].id
    }else{
        //选择树边就很简单了，之间把要选的那条边的 w 减去 S/minn 即可
        int r=S/minn;
        a[id].we-=r;
        for(int i=1;i<=m;i++)
            if(st[i])
                cout<<a[i].id<<" "<<a[i].we<<endl;
    }
}