离散数学作业07

离散数学作业

第七章练习题

第十五题

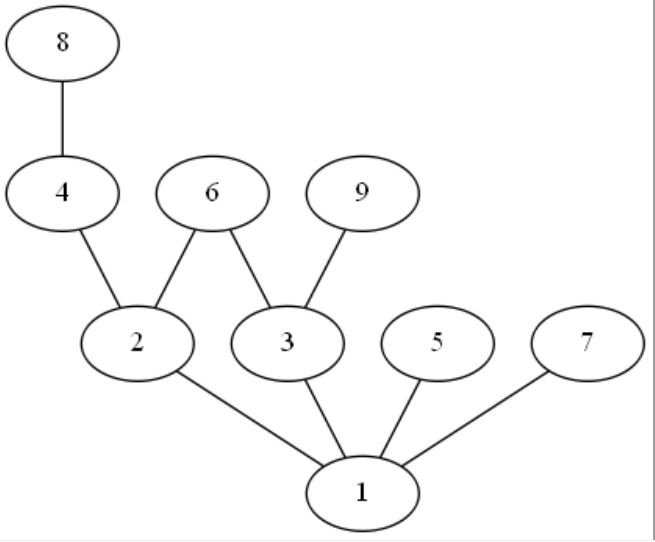
（1）图A

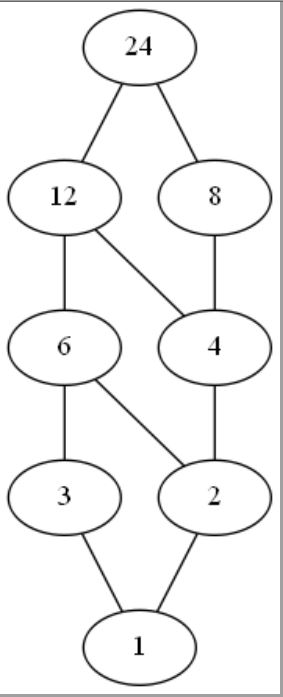
（2）图B

关系计算

求关系的定义域

//求定义域
#include <iostream>
using namespace std;
//定义一种关系
class R
{
    public:
    int s1,s2;
    //int* next;    
};
//定义一个同余关系
int  mmod(int a,int b)
{
    if (a%4==b%4)
        return 1;
    else
        return 0;
}
//定义两个非空集合A、B 
int A[10]={1,2,3,4,5,6,7,8,9,10};
int B[5]={1,2,3,4,5}; 
int main(int argc, char** argv) {
    R*g=new R[50];
    int n=0;
    for (int i=0;i<10;i++)
    {
        for (int j=0;j<5;j++)
        {
            if (mmod(A[i],B[j]))
            {
                g[i].s1=A[i];
                g[i].s2=B[j];
                n++;
                //cout<<(g[i].s1)<<endl;
            }
        }
    }
    //cout<<n<<endl;
    for (int i=0;i<n;i++)
    {
        int t=g[i].s1;
        for (int j=0;j<n;j++)
        {
            if (j!=i && g[j].s1==t)
            {
                g[j].s1=0;
            }
        }
    }
    cout<<"该关系的定义域为："<<endl;
    for (int i=0;i<n;i++)
        if (g[i].s1)
        cout<<g[i].s1<<" ";
    cout<<endl;
    delete[]g;
    return 0;
}

求关系的值域

#include <iostream>
using namespace std;
//定义一种关系
class R
{
    public:
    int s1,s2;
    //int* next;    
};
//定义一个同余关系
//模4同余 
int  mmod(int a,int b)
{
    if (a%4==b%4)
        return 1;
        //满足关系则返回1，否则返回0 
    else
        return 0;
}
//定义两个非空集合A、B 
int A[10]={1,2,3,4,5,6,7,8,9,10};
int B[5]={1,2,3,4,5}; 
int main(int argc, char** argv) {
    R*g=new R[50];
    int z[20]={0};
    int *z0=z;
    int n=0,i; 
    for (i=0;i<10;i++)
    {
        for (int j=0;j<5;j++)
        {
            if (mmod(A[i],B[j]))
            //判断是否满足关系 
            {
                g[i].s1=A[i];
                g[i].s2=B[j];
                n++;
                //cout<<(g[i].s2)<<'\n';
                z[n]=B[j];
                z0++;
            }
        }
    }
    //cout<<n<<endl;
    int m=0;
    //消除重复的项 
    for (i=0;i<n;i++)
    {
        int t=z[i];
        for (int j=0;j<n;j++)
        {
            if (j!=i && z[j]==t)
            {
                z[j]=0;
            }
        }
    }
    cout<<"该关系的值域为："<<"\n";
    for (i=0;i<n;i++)
        if (z[i])
        cout<<z[i]<<" ";
    cout<<"\n";
    delete[]g;
    return 0;
}

求关系的逆

#include <iostream>
using namespace std;
//定义一种关系
class R
{
    public:
    int s1,s2;
    //int* next;    
};
//定义一个关系
R g0[]={{1,2},{2,3},{3,1}};
int main(int argc, char** argv) {
    R g[3];
    //获取关系集的长度 
    int l=(sizeof(g0)/sizeof(R));
    for (int i=0;i<l;i++)
    {
        g[i].s1=g0[i].s2;
        g[i].s2=g0[i].s1;
    } 
    cout<<l<<'\n';
    cout<<"关系的逆为：";
    for (int i=0;i<l;i++)
    {
        cout<<"<"<<g[i].s1<<","<<g[i].s2<<">"<<",";
    } cout<<"\n";
    return 0;
}

求关系的复合运算

#include <iostream>
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
//定义一种关系
class R
{
    public:
    int s1,s2;
    //int* next;    
};
//定义两个关系
R g1[]={{1,2},{2,3},{3,1}};
R g2[]={{1,3},{2,1},{3,2}}; 
int main(int argc, char** argv) {
    R g[5];
    //获取关系集的长度 
    int l=(sizeof(g1)/sizeof(R));
    for (int i=0;i<l;i++)
    {
        for (int j=0;j<l;j++) 
        {
            g[i].s1=g1[i].s1;
            if (g2[j].s1==g1[i].s2)
                g[i].s2=g2[j].s2;
        }
    } 
    cout<<l<<'\n';
    cout<<"关系的复合运算为：";
    for (int i=0;i<l;i++)
    {
        cout<<"<"<<g[i].s1<<","<<g[i].s2<<">"<<",";
    } cout<<"\n";
    return 0;
}

判定关系是否是自反

#include <iostream>
using namespace std;
//定义一种关系
class R
{
    public:
    int s1,s2;
    //int* next;    
};
//定义一个基数为n的非空集合 a
const int n=3;
int a[n]={1,2,3}; 
//定义一个非空集合a上的关系
R g0[n]={{1,1},{2,2},{3,3}} ;
R g1[n]={{1,2},{2,3},{3,1}};
//判定函数
int reflex(R *g)
{
    int l=sizeof(g)/sizeof(R);
    int m=0;
    for (int i=0;i<l;i++)
    {
        for (int j=0;j<l;j++)
        {
            if (g[i].s1==g[i].s2 && g[i].s1==a[j])
                m++;
        }
    }
    if (m==l)
        return 1;
    else 
        return 0;
} 
int main(int argc, char** argv) {
    if (reflex(g1))
        cout<<"是自反关系"<<'\n';
    else
        cout<<"不是自反关系"<<'\n';
    return 0;
}

判定关系是否反自反

#include <iostream>
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
//定义一种关系
class R
{
    public:
    int s1,s2;
    //int* next;    
};
//定义一个非空集合 a
const int n=3;
int a[n]={1,2,3}; 
//定义一个非空集合a上的关系
R g0[n]={{1,1},{2,2},{3,3}} ;
R g1[n]={{1,2},{2,3},{3,1}};
//判定函数
int antireflex(R *g)
{
    int m=0;
    for (int i=0;i<n;i++)
    {
            if (g[i].s1!=g[i].s2)
                m++;
    }
    if (m==l)
        return 1;
    else 
        return 0;
} 
int main(int argc, char** argv) {
    if (antireflex(g0))
        cout<<"是反自反关系"<<'\n';
    else
        cout<<"不是反自反关系"<<'\n';
    return 0;
}

判定关系是否为对称

#include <iostream>
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
//定义一种关系
class R
{
    public:
    int s1,s2;
    //int* next;    
};
//定义一个非空集合 a
const int n=3;
int a[n]={1,2,3}; 
//定义一个非空集合a上的关系
R g0[n]={{1,1},{2,2},{3,3}} ;
R g1[n]={{1,1},{2,2},{3,1}};
//判定函数
int symm(R *g)
{
    R g0[n];
    //int l=sizeof(g)/sizeof(R);
    int m=0;
    for (int i=0;i<n;i++)
    {
        g0[i].s2=g[i].s1;
        g0[i].s1=g[i].s2;
    }
    for (int i=0;i<n;i++)
    {
        for (int j=0;j<n;j++)
        {
            if (g[i].s1==g0[j].s1 && g[i].s2==g0[j].s2)
                m++;
        }
    }
    if (m==n)
        return 1;
    else 
        return 0;
} 
int main(int argc, char** argv) {
    if (symm(g1))
        cout<<"是对称关系"<<'\n';
    else
        cout<<"不是对称关系"<<'\n';
    return 0;
}    

判定关系是否为反对称

#include <iostream>
using namespace std;
//定义一种关系
class R
{
    public:
    int s1,s2;
    //int* next;    
};
//定义一个非空集合 a
const int n=3;
int a[n]={1,2,3}; 
//定义一个非空集合a上的关系
R g0[n]={{1,2},{2,1},{3,3}} ;
R g1[n]={{1,1},{2,3},{3,1}};
//判定函数
int antisymm(R *g)
{
    R g0[n];
    //int l=sizeof(g)/sizeof(R);
    int m1=0,i;
    int nn=n;
    for (i=0;i<n;i++)
    {
        g0[i].s2=g[i].s1;
        g0[i].s1=g[i].s2;
    }
    for (i=0;i<n;i++)
    {
        if (g[i].s1==g[i].s2)
                nn--;
        int m2=0;
        for (int j=0;j<n;j++)
        {
            if (g[i].s1!=g[i].s2)
            {
                if ((g[i].s1==g0[j].s1 && g[i].s2==g0[j].s2)==0)
                m2++;
            }
        }
        if (m2==n)
            m1++;
    }
    if (m1==nn)
        return 1;
    else 
        return 0;
} 
int main(int argc, char** argv) {
    if (antisymm(g0))
        cout<<"是反对称关系"<<'\n';
    else
        cout<<"不是反对称关系"<<'\n';
    return 0;
}

判定关系是否为传递

//判断函数
**
 * 判断一个关系是否具有传递性。
 *  pA： 原始集合
 *  pBinaryRelationR： 卡氏积集合，该集合是一个pA上的二元关系
 *  如果pBinaryRelationR具有传递性，则返回true，否则返回false
 */ 
boolean IsTransitive(pOriginalSet pA, pCartersianSet pBinaryRelationR)
{
pOriginalSetElem First1,Second1;
pOriginalSetElem First2,Second2;
pCartersianSet pB=copyCartersianSet(pBinaryRelationR);
pCartersianSet pC=copyCartersianSet(pBinaryRelationR);
if(!isNullCartersianSet(pBinaryRelationR))
{
 for(resetCartersianSet(pC);!isEndOfCartersianSet(pC);nextCartersianSetPos(pC))
 {
  First1=getFirstElemOfOrderedCouple(getCurrentCartersianSetElem(pC));
  Second1=getSecondElemOfOrderedCouple(getCurrentCartersianSetElem(pC));
  for(resetCartersianSet(pB);!isEndOfCartersianSet(pB);nextCartersianSetPos(pB))
  {
   First2=getFirstElemOfOrderedCouple(getCurrentCartersianSetElem(pB));
   Second2=getSecondElemOfOrderedCouple(getCurrentCartersianSetElem(pB));
   if(isEqualOriginalSetElem(First2,Second1))
   {
    if(!isInCartersianSet(pBinaryRelationR,createOrderedCouple(First1,Second2)))
    return false;}
   }
  }
 }
else return true;
return true;
}

第二十题

解：
画出P的子集T的哈斯图，易得上界为3，4，5的公倍数
下界为1,最大上界为1，最小上界为60.

第二十一题

证明：
自反性：
根据定义有$x∈A，xR1x⇒xR1x$，
既有$R1≤R1$，满足自反性
反对称性：
对$R1,R2\in B,\forall x,y \in A$,若有$R1 \leqslant R2$时，仅当$R1 =R2$时，$R2 \leqslant R1$,满足反对称性
传递性：
若$R1\leqslant R2,R2\leqslant R3$,即$xR1y \Rightarrow xR3y$,即$R1 \leqslant R3$,满足传递性
综上，$<B,\leqslant>$是偏序集

六例关系

等价关系两例

1. 设$S$集合为一条水准路线中的测站点，关系$R$为精度相同的杆件测站
2. 设$S$是实数域上的矩阵组成的集合，关系$R$为矩阵$A$,$B$的行数列数相同且同秩

偏序关系两例

3、设$P$集合中的每一个元素都是一位公司职员，关系$R$为上司给下级分派任务
4、设$L$为我们国家的大地控制网中的各级导线，关系$C$为从已知点设计测量路线对未知地域的测量

5、 设$L$为数据结点集，关系$S$为链表关系。从头结点开始，一个指向一个
6、设$S$为决策分类树集合，关系$E$为分类结果相同的决策分类树