三自由度直升机系统控制仿真

三自由度直升机 PID控制 LQR最优控制

---

1.系统概述

三自由直升机系统由基座、平衡块和螺旋桨等部分组成，平衡杆以基座为支点，做俯仰和转动动作。螺旋桨和平衡块分别安装在平衡杆的两端。螺旋桨旋转产生的升力可以使平衡杆以基座为支点做俯仰运动，利用两个螺旋桨的速度差可以使平衡杆以基座为轴做旋转运动。平衡杆的旋转轴、俯仰轴和螺旋桨的横侧轴都都分别安装了编码器，用来测量平衡杆俯仰轴、旋转轴和螺旋桨横侧轴的数据。两个螺旋桨分别由两个直流无刷电机驱动，为螺旋桨提供动力。通过调节安装在平衡杆另一侧的平衡块可以减少螺旋桨电机的出力。安装在基座的集电环保证了系统本体和电控箱之间的信号传输不受直升机转动的影响。

---

2.系统建模

根据系统的特性，将它分为三个自由度分别建模。

2.1俯仰轴

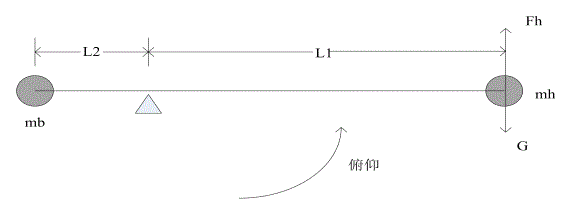
由图可知，俯仰轴的转矩由两个螺旋桨电机产生的升力$F_1$和$F_2$所产生，故螺旋桨的升$F_h=F_1+F_2$。当升力$F_h$大于螺旋桨的和重力G时，$G=G_1+G_2$，则直升机上升；反之，直升机下降。
假设直升机悬在空中，并且俯仰角为零度，根据静平衡假设，列写力学方程

$$J_e \cdot \ddot{\epsilon}=l_1F_h-l_1G+l_2 G_b=l_1(F_1+F_2)l_1G+l_2 G_b$$
其中$G_b$为平衡块重力。由于螺旋桨的升力由电机提供，假设$V_1$和$V_2$是螺旋桨两个电机的电压，其与升力呈线性关系
$$F_1=K_cV_1$$
$K_c$为螺旋桨电机的升力系数。令俯仰轴产生的有效重力矩为$T_g$,
并令$V_s=V_1+V_2$,得到
$$J_e \cdot \ddot{\epsilon}=K_cl_1(V_1+V_2)-T_g=K_cl_1V_s-T_g\tag{1}$$

通过资料，确定我们会用到的电气参数如下表

代号	含义	大小	单位
$J_e$	俯仰轴转动惯量	0.7663	$kg\cdot m^2$
$J_t$	旋转轴转动惯量	0.7663	$kg\cdot m^2$
$J_p$	横侧轴转动惯量	0.0266	$kg\cdot m^2$
$m_h$	螺旋桨本体质量	1.500	$kg$
$m_b$	平衡块质量	2.120	$kg$
$l_1$	螺旋桨到支点距离	0.64	$m$
$l_2$	支点到平衡块距离	0.25	$m$
$l_p$	螺旋桨到横侧轴支点的距离	0.17	$m$
$K_c$	电机力常数	0.50	$N/V$
$F_h$	螺旋桨悬浮力	0.69	单位
$m_g$	螺旋桨等效质量		$kg$
$\dot{\varepsilon}$、$\dot{P}$	俯仰轴、横侧轴的转动加速度
$\gamma$	旋转轴旋转速度		$rad/s$

2.2横侧轴

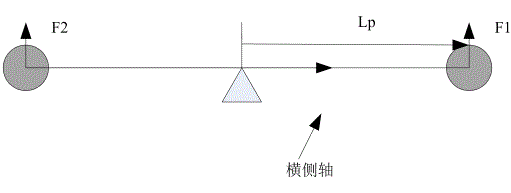
如图 所示，横侧轴由两个螺旋桨产生的升力控制，如果$F_1$产生的升力大于$F_2$产生的升力，则螺旋桨本体就会产生倾斜，这样就会产生一个侧向力，使直升机围绕基座旋转。

$$J_2 \cdot \ddot{P}=F_1 l_p - F_2 l_p$$
同理，螺旋桨的升力与电机电压呈线性关系，因此，令$V_1$和$V_2$是螺旋桨两个电机的电压，并且$V_d=V_1-V_2$,得到
$$J_2 \cdot \ddot{P}=K_c l_p (V_1-V_2)=K_c l_P V_d\tag{2}$$

2.3旋转轴

当横侧轴倾斜时，会产生一个垂直于两个螺旋桨所在平面的侧方向升力$F_h$，如图所示。该侧方向分升力在竖直平面内的分力可以让直升机本体在空中出于悬停状态。在水平面的另一个分力是旋转轴在水平面内运动的动力来源，旋转轴$F_h$在的水平方向升力分量的作用下不断加速直至达到给定的参考旋转速度。

$$J_t \dot{\gamma}=F_H (sinp)l_1$$
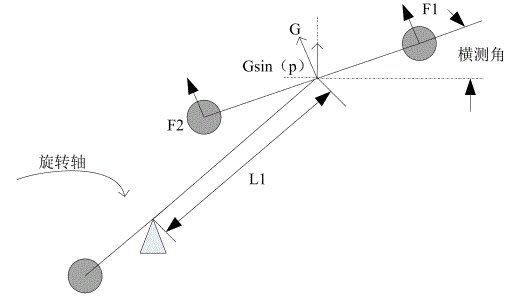
如果横侧轴很小，则侧方向升力$F_h$的大小约等于两个螺旋桨的等效重力$G$,即
$$F_h=F_1+F_2=K_cV_1+K_cV_2=-G$$
这样就可以将化简成
$$J_t \dot{\gamma}=-G (sinp)l_1\tag{3}$$
由式（1）（2）（3）可知，俯仰角的加速度是加在两个螺旋桨电机的电压和的函数；横侧轴角加速度是两个电机电压差的函数；当横侧角较小时，旋转轴的角加速度和横侧角可以看成比例关系。

---

3.控制系统设计

3.1俯仰轴

3.1.1俯仰轴系统
对于俯仰轴动力方程（1）式，忽略重力扰动力矩$T_g$,可以得到线性系统

$$J_e \cdot \ddot{\epsilon}=K_cl_1(V_1+V_2)=K_cl_1V_s\tag{4}$$
将电压和信号$V_s$作为控制系统输入，俯仰角角度$\varepsilon$为控制系统输出,因此俯仰轴系统的传递函数写为
$$G_1(s)=\frac{C(s)}{Y(s)}=\frac{K_cl_1}{J_es^2}\tag{5}$$
其框图如下

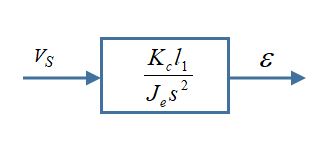
易知此系统为二型系统，且系统不稳定。
3.1.2俯仰控制器设计
可以设计PD校正。
其中$\varepsilon$为实际俯仰角，$\varepsilon_c$代表参考俯仰角，有控制关系
$$V_s=K_{ep}(\varepsilon_c-\varepsilon)-K_{ed}\dot{\varepsilon}\tag{6}$$
系统的闭环传递函数为：
$$\frac{\varepsilon(s)}{\varepsilon_c(s)}=\frac{\frac{K_cK_{ep}l_1}{J_e}}{s^2+\frac{K_cK_{ed}l_1}{J_e}s+\frac{K_cK_{ep}l_1}{J_e}}\tag{7}$$
式子中的分母可看作二阶系统的一般形式：$s^2+2\zeta\omega_ns+{\omega_n}^2$,且二阶系统的峰值时间为$t_p=\frac{\pi}{\omega_n\sqrt{1-{\zeta}^2}}$,因此可以通过选择所期望的性能指标$_p$和$t_p$和$\zeta$来确定期望的响应。

由此，通过MATLAB里的SIMULINK模块仿真俯仰轴的角度控制。

假定给定性能指标，如下表所示，则可以通过调整$K_1$和$K_2$的值，实现固定要求的系统控制。

三轴	$t_p$	$\zeta$
俯仰轴	2	0.707
旋转轴	1.5	0.707
横侧轴	8	0.707

假定俯仰角输入值为30，通过simulink仿真PD控制和未控制的曲线如下图

可见原二阶系统发散，通过PD校正后系统稳定。

3.2横侧轴

3.2.1横侧轴系统
将电压和信号$V_d$作为控制系统输入，俯仰角角度$p$为控制系统输出,因此俯仰轴系统的传递函数写为。由式（2）可得横侧轴被控模型。

$$G_2(s)=\frac{C(s)}{Y(s)}=\frac{K_cl_p}{J_ps^2}\tag{8}$$

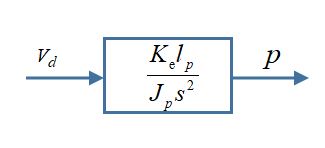
它与俯仰轴控制系统是一个类似的二阶不稳定系统。
3.2.2横侧控制器设计
同理设计PD控制器。
$$V_d=K_{pp}(p_c-p)+K_{pd}\dot{p}\tag{9}$$

校正以后的系统闭环传递函数为
$$\frac{p(s)}{p_c(s)}=\frac{\frac{K_cK_{pp}l_p}{J_p}}{s^2+\frac{K_cK_{pd}l_p}{J_p}s+\frac{K_cK_{pp}l_p}{J_p}}\tag{10}$$
同理可以通过选择$K_pp$和$K_pd$来实现前面指标表格中期望的$t_p$和$\zeta$.

3.3旋转轴

3.3.1旋转轴系统
由（3）式可知旋转轴动力学方程，因为其含有正弦项，对其进行线性化，在横侧角很小时，可以有$\sin p=p$,假定这个线性化范围$p<20^\omicron$

$$J_t \dot{\gamma}=F_hpl_1\tag{11}$$

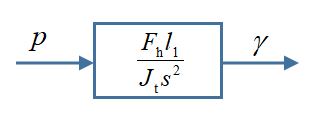
3.3.2旋转控制器设计
由（2）(3)易知道横侧轴和旋转轴的控制是耦合的，改变直升机横侧角的倾斜角的大小就可以控制直升机的旋转速度。因此，根据横侧轴以及旋转轴的相关性，将他们合成为一个系统进行设计。

其中内环为横侧轴的PD控制，外环为旋转轴的PID控制。
假定输入的旋转角为20，通过SIMULINK进行系统仿真，获得上述控制下的横侧角和旋转角仿真曲线。

横侧角经过PD控制后回到零位置平衡，而旋转角经过PID控制后达到预定值，并且横侧角的调节要快于旋转角。

---

4.LQR最优控制

PID控制中，我们是根据经典控制论，利用全状态反馈控制，凭经验在选取$t_p$和$\zeta$，确定定值系数进行系统设计。
现在从多变量的角度，利用现代控制理论设计LQR控制器。

4.1LQR控制简介[1]

LQR (linear quadratic regulator)即线性二次型调节器 ,其对象是现代控制理论中以状态空间形式给出的线性系统 ,而目标函数为对象状态和控制输入的二次型函数。LQR最优设计是指设计出的状态反馈控制器 K要使二次型目标函数J 取最小值,而 K由权矩阵Q 与 R 唯一决定,故此 Q、 R 的选择尤为重要。LQR理论是现代控制理论中发展最早也最为成熟的一种状态空间设计法。特别可贵的是 ,LQR可得到状态线性反馈的最优控制规律 ,易于构成闭环最优控制。

Q为性能指标函数对于状态量的权阵，为对角阵，元素越大，意味着该变量在性能函数中越重要。要求性能函数求最小，也就是说该状态的约束要求高。
R阵为控制量的权重，对角阵，同样，对应的元素越大，这意味着，控制约束越大。
其具体的模型推导已经是成熟的理论，在此不再赘述。

4.2LQR控制器设计

已知系统的状态空间模型

$$\begin{cases} \dot{x} =Ax+Bu\\ y=Cx+Du \\ \end{cases}\tag{12}$$
选取系统状态变量
$$x^\intercal=[x_1,x_2,x_3,x_4,x_5]=[\epsilon,p,\dot{\epsilon},\dot{p},\gamma]$$
系统输入
$$u^\intercal=[V_1,V_2]$$
联立第一节模型中的(1)(2)(3)式，可以获得状态空间模型如下
$$\begin{bmatrix}\dot{\epsilon}\\\dot{p} \\ \ddot{\epsilon}\\ \ddot{p}\\ \dot{\gamma}\end{bmatrix}=\begin{bmatrix}0&0&1&0&0\\0&0&0&1&0\\ 0&0&0&0&0\\0&0&0&0&0\\ 0&\frac{F_hl_1}{J_t}&0&0&0\end{bmatrix}\begin{bmatrix}\epsilon\\p\\ \dot{\epsilon}\\ \dot{p}\\ \gamma\end{bmatrix}+\begin{bmatrix}0&0\\0&0\\\frac{K_cl_1}{J_e}&\frac{K_cl_1}{J_e}\\ \frac{K_cl_p}{J_p}&-\frac{K_cl_p}{J_p}\\ 0&0\end{bmatrix}\begin{bmatrix}V_1\\V_2\end{bmatrix}$$
$$y=\begin{bmatrix}1&0&0&0&0\\0&1&0&0&0\\ 0&0&0&0&1\end{bmatrix}x\tag{13}$$
代入前文中的电气参数，得到具体的系数矩阵
$$A=\begin{bmatrix}0&0&1&0&0\\0&0&0&1&0\\ 0&0&0&0&0\\0&0&0&0&0\\ 0&0.585&0&0&0\end{bmatrix}$$
$$B=\begin{bmatrix}0&0\\0&0\\0.424&0.424\\ 3.198&-3.198\\ 0&0\end{bmatrix}$$

线性二次型即是求最优控制$u(t)$,使得性能指标

$$J=\int_0^\infty {(x^\intercal Qx+u^\intercal Ru)} \,{\rm d}x\tag{14}$$
Q为正定（或半正定）厄米特或实对称矩阵；R为正定厄米特矩阵或实对称矩阵。矩阵Q和R确定了误差和能量损耗的相对重要性，并且假设控制向量无约束的。
根据一般原则，选定Q和R的参数
$$R=diag（[5,5]）$$
$$Q=diag（[300,300,1,1,1]）$$

通过MATLAB对我们所需的增益矩阵K进行求解，并对

A=[0 0 1 0 0;
0 0 0 1 0;
0 0 0 0 0;
0 0 0 0 0;
0 0.585 0 0 0];
B=[0 0;
0 0;
0.424 0.424;
3.198 -3.198;
0 0];
C=[1 0 0 0 0;
0 1 0 0 0;
0 0 0 0 1];
D=[0];%输入系数矩阵
Q11=300;Q22=300;Q33=1,Q44=1;Q55=1;
Q=[Q11 0 0 0 0;
0 Q22 0 0 0;
0 0 Q33 0 0;
0 0 0 Q44 0;
0 0 0 0 Q55];
R=[5 0;
0 5];%输入性能指标矩阵
P=care(A,B,Q,R)
K=inv(R)*B'*P%二次型最优控制求解

得到的计算输出如下

Q33 =

     1


P =

  197.6207         0   64.5899         0         0
         0   74.3574         0    8.6346    4.2742
   64.5899         0   42.5477         0         0
         0    8.6346         0    2.1133    0.4944
         0    4.2742         0    0.4944   29.8535


K =

    5.4772    5.5227    3.6080    1.3516    0.3162
    5.4772   -5.5227    3.6080   -1.3516   -0.3162

得到状态方程的反馈增益

$$K=\begin{bmatrix}k_{11}&k_{12}&k_{13}&k_{14}&k_{15}\\k_{21}&k_{22}&k_{23}&k_{24}&k_{25}\end{bmatrix}=\begin{bmatrix}5.4772&5.5227&3.6080&1.3513&0.3162\\5.4772&-5.5227&3.6080&-1.3513&-0.3162\end{bmatrix}$$
利用反馈增益系数，我们可以进一步地设计PID控制器。
下面我们使用MATLAB直接对其仿真，其matab指令如下。
假设我们的输入初值为
$$x^\intercal（0）=[x_1,x_2,x_3,x_4,x_5]=[0.2,0.1,0,0,0]$$

V1=0.4;V2=0.2;
Eleva=0.2;dEleva=0;
Travel=0.1;dTravel=0;
Rotate=0;dRotate=0;
tf=5;
dt=0.001;
for i=1:tf/dt

    ddEleva=0.424*(V1+V2);
    ddTravel=3.198*(V1-V2);
    dRotate=0.585*Eleva;

    dEleva=ddEleva*dt+dEleva;
    Eleva=dEleva*dt+Eleva;
    dTravel=ddTravel*dt+dTravel;
    Travel=dTravel*dt+Travel;
    Rotate=dRotate*dt+Rotate;

    V1=-(K(1,1)*Eleva+K(1,2)*Travel+K(1,3)*dEleva+K(1,4)*dTravel+K(1,5)*Rotate);
    V2=-(K(2,1)*Eleva+K(2,2)*Travel+K(2,3)*dEleva+K(2,4)*dTravel+K(2,5)*Rotate);

    t=i*dt;
    tp(i)=t;
    Eleva_p(i)=Eleva;
    Travel_p(i)=Travel;
    Rotate_p(i)=Rotate;
    V1_p(i)=V1;
    V2_p(i)=V2;
end
figure(1)   
subplot(3,1,1);plot(tp,Eleva_p);grid on;xlabel('t'),ylabel('俯仰角')， title('LQR直升机俯仰角、横侧角、旋转角仿真曲线');
subplot(3,1,2);plot(tp,Travel_p);grid on;xlabel('t'),ylabel('横侧角');
subplot(3,1,3);plot(tp,Rotate_p);grid on;xlabel('t'),ylabel('旋转角');
figure(2)
subplot(2,1,1);plot(tp,V1_p);grid on;xlabel('t'),ylabel('V1')，title('直升机两个电机输入信号仿真曲线');
subplot(2,1,2);plot(tp,V2_p);grid on;xlabel('t'),ylabel('V2');

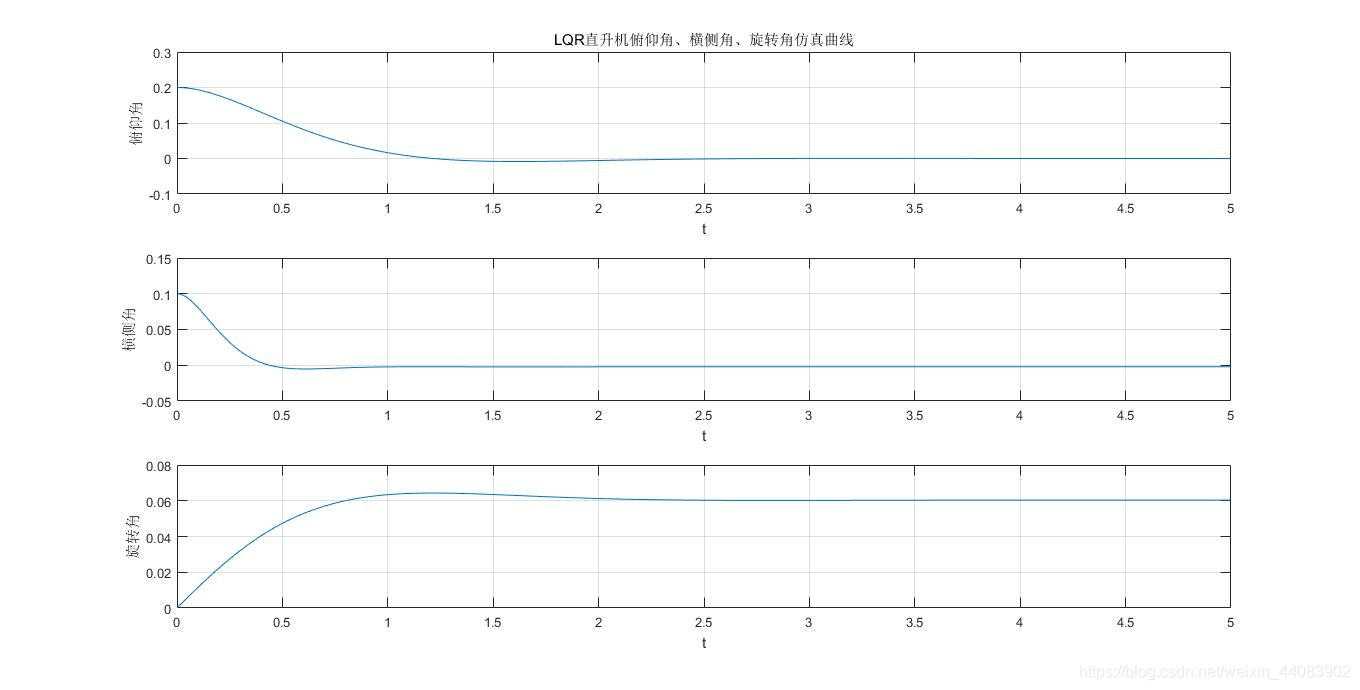
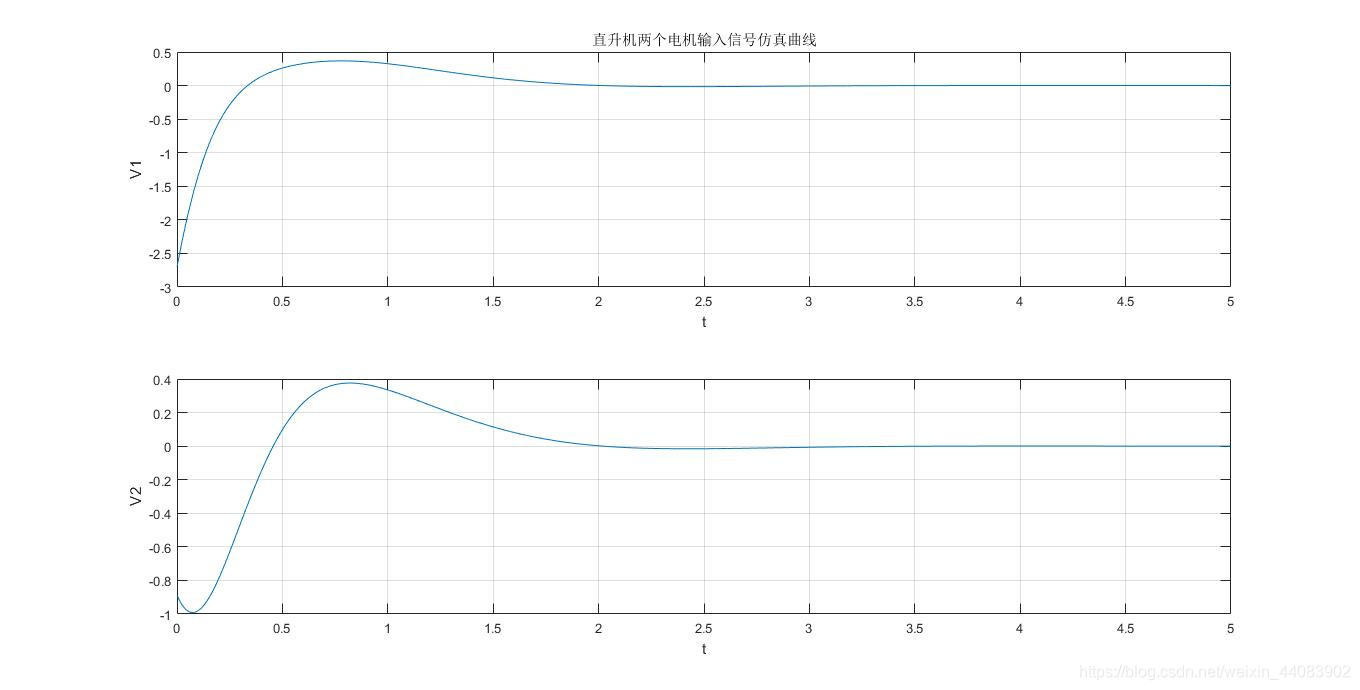
得到的仿真曲线如下

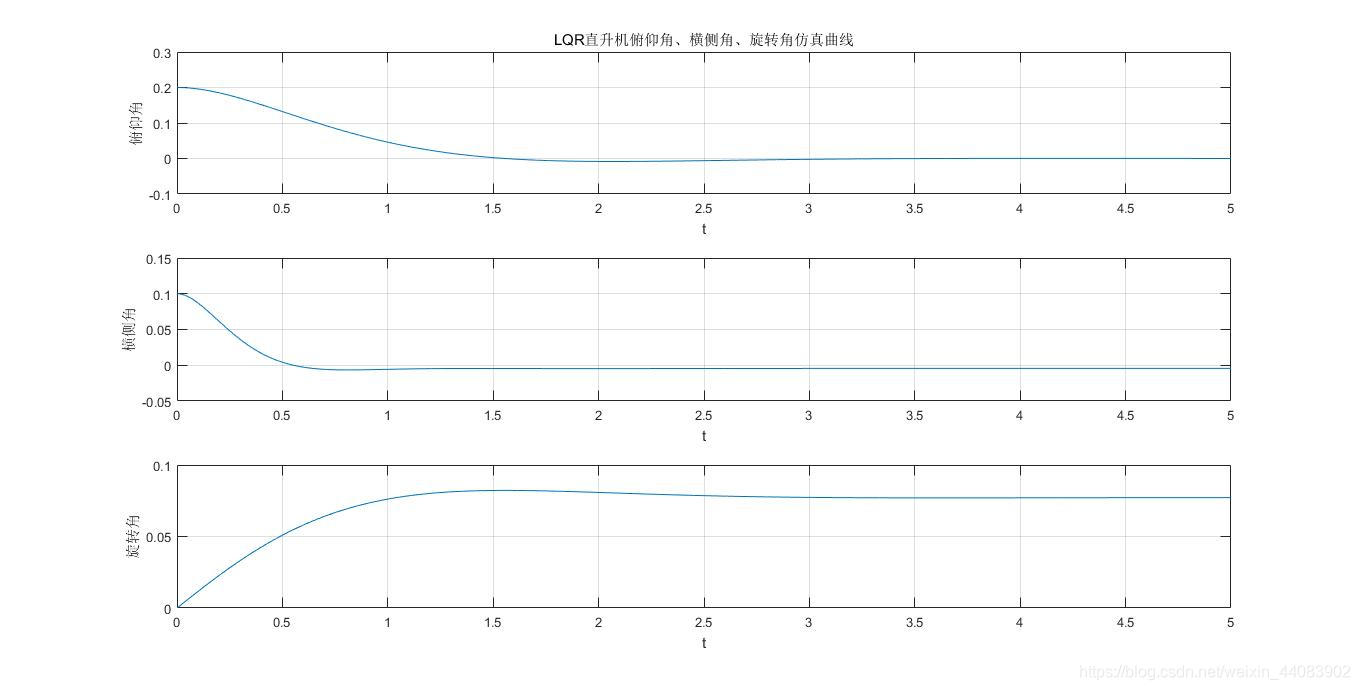
从图中可以看出，在给定了前述初值情况下，LQR结果的控制器控制效果良好：俯仰角回到平衡点的调节时间约为1.5s；横侧角回到稳态误差的调节世界小于1s；旋转角的调节滞后于横侧角，由于旋转角速度受横侧角比例控制，因此在2.5s左右进入一个不一定为零的恒定值附近，能量消耗控制地较小。

最后，进一步对LQR的两个权值矩阵进行试探。

如果只增大R的权值

$$R_t=diag（[20,20]）$$
$$Q=diag（[300,300,1,1,1]）$$
则增益输出

K =

2.7386    2.7703    2.5464    0.9441    0.1581
2.7386   -2.7703    2.5464   -0.9441   -0.1581

反馈增益明显减小，仿真曲线如下


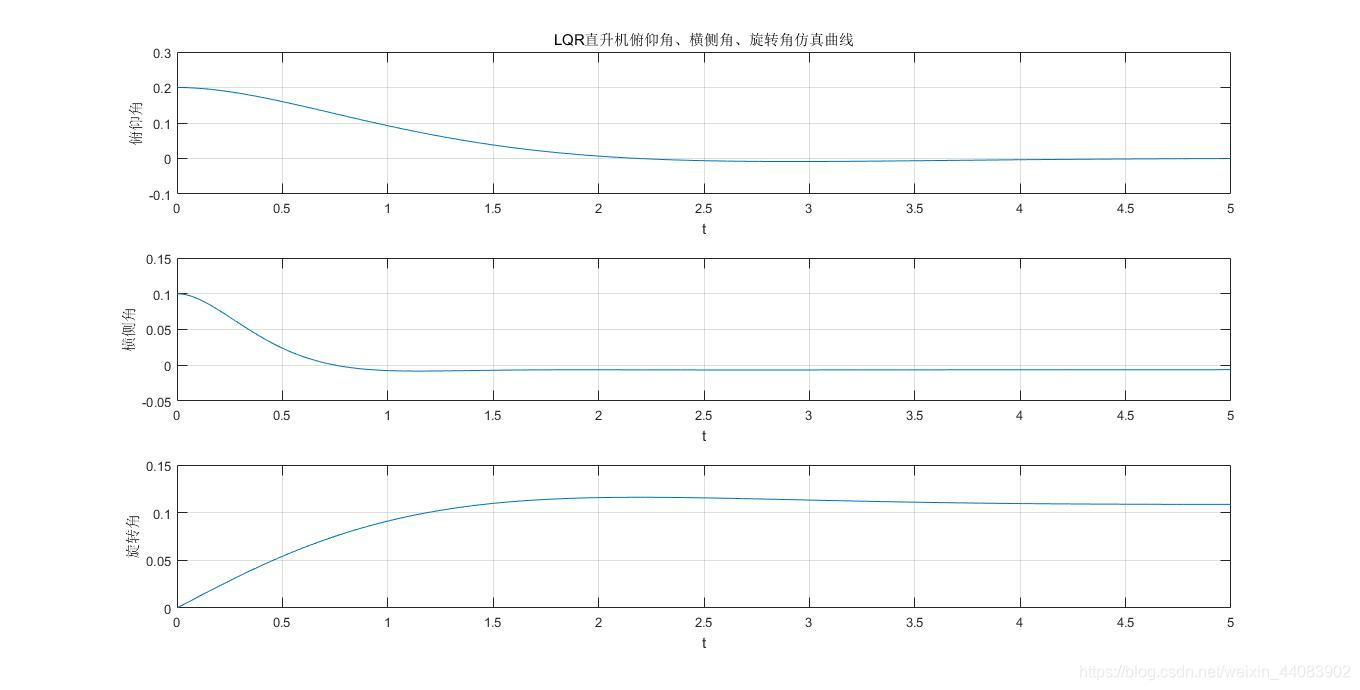
可见系统的动态性能变差，信号变幅减小，调节消耗的能量减小。

如果只增大Q的权值

$$R=diag（[5,5]）$$
$$Q_t=diag（[800,800,1,1,1]）$$
则增益输出

 K =

8.9443    8.9795    4.6038    1.7052    0.3162
8.9443   -8.9795    4.6038   -1.7052   -0.3162

仿真曲线如下


可见系统的快速性有所提升，但是消耗能量明显变大。

因此在LQR的控制中，选取Q和R权值矩阵，表征着控制的能量消耗和性能改善也是相互影响和制约：想要获得好的动态性能，就要消耗更多的能量；节省能量则会以控制质量的下降为代价。

参考文献

1杨慧萍,高贯斌,那靖. 三自由度直升机实验平台及姿态跟踪控制器设计[J]. 机械与电子,2015,(05):69-72.
2吴琼,王强,兰文宝,刘思久. 基于模糊自适应PID三自由度直升机控制器的研究[J]. 黑龙江大学工程学报,2014,5(02):87-93.
3张乐,吴金男,毕少杰. 基于模糊PID的直升机模型飞行姿态控制[J]. 控制工程,2014,21(03):387-390+394.
4丁春龙. 三自由度直升机建模及控制方法研究[D].哈尔滨理工大学,2014.
5葛金来,张承慧,崔纳新. 模糊自整定PID控制在三自由度直升机实验系统中的应用[J]. 信息与控制,2010,39(03):342-347.

---

相关个人链接
本报告网页链接
CSDN此篇专供用图网页