排序算法

数据结构与算法

一、概述

1.时间复杂度：
一般而言，对于一个排序，比较好的性能是O(NlogN)，坏的性能是O(n^2)，最理想的性能是O(n)。仅使用一个抽象关键比较运算的排序算法总平均上至少需要O(NlogN)。

2.稳定性：
稳定排序算法会让原本有相等键值的记录维持相对次序。也就是说，如果一个排序算法是稳定的，当有两个相等键值的记录和R和S，且在原本的列表中R出现在S之前，在排序过后的列表中R依然在S前面。

3.分类：

1）根据排序的数据是否全部在内存中：内部排序和外部排序。
2）根据排序方法的稳定性：稳定排序和不稳定排序
3）根据排序的方法：插入(插入排序、希尔排序)、选择(选择排序、堆排序)、交换(冒泡排序、快速排序)、合并(归并排序)等

4.内排序算法分类：

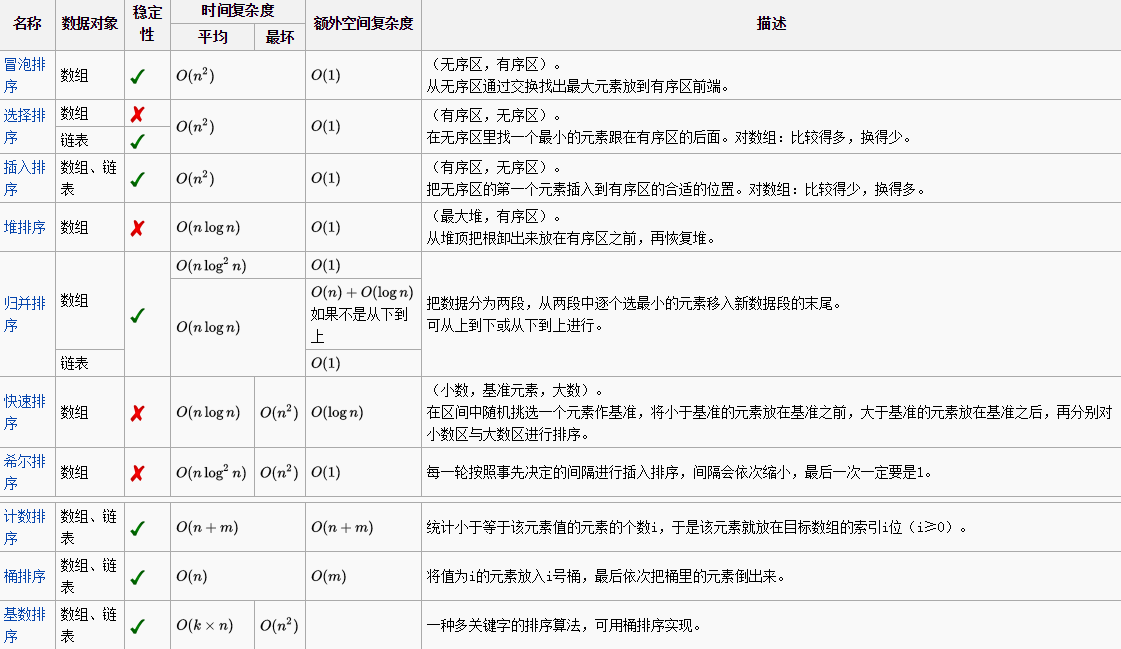
1）简单排序算法，时间复杂度为O(n^2)：冒泡排序、插入排序和简单选择排序。性能比较：直接插入排序 > 简单选择排序 > 冒泡排序
2）改进算法，时间复杂度为O(nlogn)：堆排序、希尔排序、归并排序和快速排序
3）非基于比较的算法，时间复杂度为O(n)：计数排序、桶式排序和基数排序

二、内排序

1.冒泡排序

1）说明：对当前还未排好序的数，自上而下对相邻两个数依次比较和调整，让较大的数往下沉，较小的数往上冒(故称为冒泡)。

2）实现：

public static void bubbleSort(int[] a){
    int temp;//中间数
    for(int i = 0; i < a.length - 1; i++){//i表示交换的次数，总共交换a.length - 1次就足够了
        for(int j = 0; j < a.length - 1 - i; j++){
            if(a[j] > a[j+1]){//相邻两数交换，使得最大值往最后走
                temp = a[j];
                a[j] = a[j+1];
                a[j+1] = temp;
            }
        }
    }
}

3）改进：设置标记，如果某趟排序过程中未发生任何交换，说明数据已经是有序的了，就不用再进行排序了

public static void bubbleSort(int[] a){
    boolean flag = true;//设置标记
    int temp;
    for(int i = 0; i < a.length - 1 && flag; i++){
        flag = false;
        for(int j = 0; j < a.length - 1 - i; j++){
            if(a[j] > a[j+1]){
                temp = a[j];
                a[j] = a[j+1];
                a[j+1] = temp;
                flag = true;
            }
        }
    }
}

2.简单选择排序

1）说明：选择排序的基本思想是每一趟在n-i+1个记录中选择关键字最小的记录作为序列的第i个记录。
简单选择排序比较的次数比较多，但移动数据的次数比较少，性能优于冒泡排序

2）实现：

public static void selectSort(int[] a){
    int min, temp;//min表示最小记录的位置，temp为了暂存值
    for(int i = 0; i < a.length; i++){
        min = i;
        for(int j = i + 1; j < a.length; j++){
            if(a[min] > a[j]){
                min = j;
            }
        }
        if(min != i){
            temp = a[min];
            a[min] = a[i];
            a[i] = temp;
        }
    }
}

3.直接插入排序

1）说明：基本操作是将一个记录插入到已经排好序的有序表中，从而得到一个新的、记录数加1的有序表。性能优于冒泡排序和简单选择排序。

2）实现：

public static void insertSort(int[] a){
    int temp, i, j;
    for(i = 1; i < a.length; i++){
        if(a[i] < a[i - 1]){//说明顺序不对，需要排序
            temp = a[i];
            for(j = i - 1; j >= 0 && a[j] > temp; j--){
                a[j + 1] = a[j];//逐个往后腾出位置
            }
            a[j+1] = temp;
        }
    }
}

4.希尔排序

1）说明：也是利用插入进行排序，与直接插入排序不同的是：将关键字较小的记录跳跃式地往前移动，从而使得每次完成一轮循环后，整个序列就变得有序一些。希尔排序的关键并不是随便分组后各自排序，而是将相隔某个增量的记录组成一个子序列，实现跳跃式的移动，使得时间复杂度小于O(n^2)

2）实现：

public static void shellSort(int[] a){
    int i, j, temp;
    int increment = a.length;
    do{
        increment = increment/3 + 1;//确定增量的大小
        for(i = increment; i < a.length; i++){
            if(a[i] < a[i - increment]){//这部分与插入排序的思想一致，只是插入排序的增量总是1
                temp = a[i];
                for(j = i - increment; j >= 0 && temp < a[j]; j -= increment){
                    a[j+increment] = a[j];
                }
                a[j+increment] = temp;
            }
        }
    }while(increment > 1);
}

5.堆排序

1）说明：堆是一种完全二叉树，其根结点一定是堆中所有结点最大值或者最小值。堆排序就是利用堆进行排序的方法，其基本思想是：将待排序的序列构造成一个大顶堆，此时整个序列的最大值就是堆顶的根结点，将它移走（与末尾元素交换，此时末尾元素就是最大值了），然后将剩余的n-1个元素重新构造成一个堆，如此循环下去，便能得到一个有序序列了。

2）实现：

public class HeapSort {
    private static int[] sort = new int[]{1,0,10,20,3,5,6,4,9,8,12,17,34,11};
    public static void main(String[] args){
        System.out.println("Before Build: " + Arrays.toString(sort));
        buildMaxHeap(sort, sort.length);
        System.out.println("After Build:  " + Arrays.toString(sort));
        heapSort(sort, sort.length);
        System.out.println("After Sort:  " + Arrays.toString(sort));
    }
    public static void heapSort(int[] arr, int size){
        //构建最大堆
        buildMaxHeap(arr, size);
        //交换元素
        for(int i = size - 1; i > 0; i--){
            //将堆顶元素与数组最后一个元素交换
            swap(arr, 0, i);
            //重新构建大顶堆
            buildMaxHeap(arr, i);//这里不能是i - 1，与buildMaxHeap有关
        }
    }
    /**
     * 创建最大堆
     * @param arr
     * @param size
     */
    public static void buildMaxHeap(int[] arr, int size){
        for(int i = size / 2; i >= 0; i--){
            maxHeapify(arr, size, i);
        }
    }
    /**
     * 调整无序区（使其部分成为二叉堆）
     * @param arr
     * @param size
     * @param index
     */
    public static void maxHeapify(int[] arr, int size, int index){
        int leftSonIndex = 2*index + 1;
        int rightSonIndex = 2*index + 2;
        int temp = index;
        if(index <= size / 2){
            if(leftSonIndex < size && arr[temp] < arr[leftSonIndex]){
                temp = leftSonIndex;
            }
            if(rightSonIndex < size && arr[temp] < arr[rightSonIndex]){
                temp = rightSonIndex;
            }
            if(temp != index){
                swap(arr, index, temp);
                maxHeapify(arr, size, temp);
            }
        }
    }
    /**
     * 交换数组中两数的值
     * @param arr
     * @param i
     * @param j
     */
    public static void swap(int[] arr, int i, int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

3）评价：运行时间主要是消耗在初始构建堆和重建堆时的反复筛选上。时间复杂度为O(nlogn)。不适用于排序序列个数较少的情况

6.归并排序

1）说明：归并是指将两个或两个以上的有序表组合成一个有序表。归并排序利用归并的思想将无序序列中的元素两两排序后再合并，最终获得一个有序序列。归并排序利用了分治算法的思想。

2）实现：

public class MergeSort {
    public static void main(String[] args) {
        int[] arr = {26, 5, 98, 108, 28, 99, 34, 56, 64, 1};
        mergeSort(arr);
        //打印排序好的数组
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }
    /**
     * 对外接口：最终的排序方法
     * @param a
     */
    public static void mergeSort(int[] a){
        System.out.println("开始排序");
        sort(a, 0, a.length - 1);
    }
    /**
     * 递归地将数组分成小的片段
     * @param a
     * @param left
     * @param right
     */
    private static void sort(int[] a, int left, int right){
        if(left >= right){
            return;
        }
        int mid = (left + right) / 2;
        sort(a , left, mid);
        sort(a, mid + 1, right);
        merge(a, left, mid, right);
    }
    /**
     * 合并两个已经排序好的序列
     * @param a
     * @param left
     * @param mid
     * @param right
     */
    private static void merge(int[] a, int left, int mid, int right){
        //中间数组
        int[] temp = new int[a.length];
        int r1 = mid + 1;
        int tIndex = left;
        int cIndex = left;
        //把数组中一部分数据排序好
        while(left <= mid && r1 <= right){
            if(a[left] <= a[r1]){
                temp[tIndex] = a[left];
                tIndex++;
                left++;
            }else{
                temp[tIndex] = a[r1];
                tIndex++;
                r1++;
            }
        }
        //把左边或者右边还剩下的数据拷贝到新的数组中
        while(left <= mid){
            temp[tIndex] = a[left];
            tIndex++;
            left++;
        }
        while(r1 <= right){
            temp[tIndex] = a[r1];
            tIndex++;
            r1++;
        }
        //将排序好的数组拷贝到原来的数组
        while(cIndex <= right){
            a[cIndex] = temp[cIndex];
            cIndex++;
        }
    }
}

3）评价：归并排序是一种比较占用内存，但效率高且稳定的算法。其时间复杂度为O（nlogn），空间复杂度为O（n + logn）

7.快速排序

1）说明：通过一趟排序将待排序记录分割成独立的两部分，其中一部分记录的关键字均比另一部分的记录的关键字小，则可分别对这两部分记录继续进行排序，以达到整体有序的目的。

2）实现：

public class QuickSort {
    public static void main(String[] args) {
        int[] arr = {55, 5, 98, 108, 28, 99, 34, 56, 64, 1};
        qSort(arr, 0, 9);
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }
    /**
     * 对外接口
     * @param arr
     */
    public static void quickSort(int[] arr){
        qSort(arr, 0, arr.length - 1);
    }
    /**
     * 分治、递归地对数组进行处理
     * @param arr
     * @param low
     * @param high
     */
    private static void qSort(int[] arr, int low, int high){
        if(low < high){
            //确定基准值
            int pivot = partition(arr, low, high);
            //递归排序左右数组
            qSort(arr, low, pivot - 1);
            qSort(arr, pivot + 1, high);
        }
    }
    /**
     * 依据基准值给数组大致划分为两部分，左边的数都小于基准值，右边的数都大于基准值
     * @param arr
     * @param low
     * @param high
     * @return
     */
    private static int partition(int[] arr, int low, int high){
        //把数组的第一个数当做基准值
        int pivot = arr[low];
        //将数组中大于和小于等于基准值的数据分开
        while(low < high){
            //从数组右侧开始，如果某数大于基准值，则high减小一位，如果数组小于或等于基准值，则跳过该步骤
            while(low < high && arr[high] > pivot){
                high--;
            }
            //如果数组右侧某值小于基准值，则将数值的值赋值给左侧相应位置
            if(low < high){
                arr[low] = arr[high];
                low++;
            }
            //从数组左侧开始，如果某数小于基准值，则low增加一位，如果大于基准值，则跳过该步骤
            while(low < high && arr[low] <= pivot){
                low++;
            }
            //如果数组右侧某值大于基准值，则将数值的值赋值给右侧相应位置
            if(low < high){
                arr[high] = arr[low];
                high--;
            }
        }
        //扫描完成，基准值到位
        arr[low] = pivot;
        //返回基准值的位置
        return low;
    }
}

8.计数排序

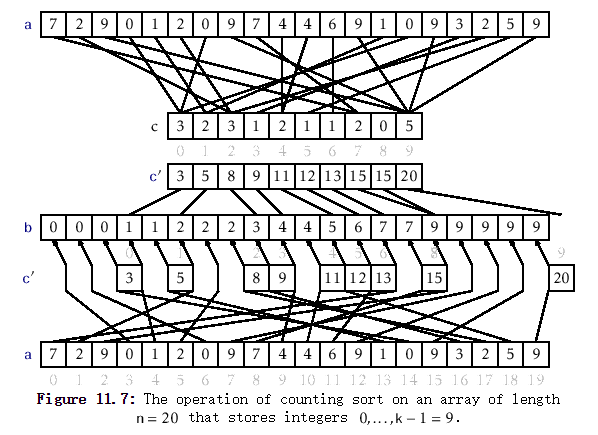
1）说明：计数排序使用一个额外的数组C，其中第i个元素的值是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。

2）实现：

public static int[] countSort(int[] a, int k) {//k表示数组中最大值max+1
    //创建辅助数组
    int c[] = new int[k];
    //c[i]表示i的个数
    for (int i = 0; i < a.length; i++){
        c[a[i]]++;
    }
    //c[i]表示i的位置(从后面开始数，第一个i的位置)    
    for (int i = 1; i < k; i++){
        c[i] += c[i-1];
    }
    //创建输出数组   
    int b[] = new int[a.length];
    //扫描原始数组a,并将a[i]放到相应的位置
    for (int i = a.length-1; i >= 0; i--){
        //c[a[i]]表示从右边开始，a[i]所处的第一个位置，每次赋值后，c[a[i]]要减一
        b[--c[a[i]]] = a[i];
    }
    return b;
}

改进：

public static int[] countSort(int[] a){
    //最后排序后返回的数组
    int[] b = new int[a.length];
    //确定待排序的数组中的最大值和最小值，确定中间数组C的大小
    int max = a[0];
    int min = a[0];
    for (int i : a) {
        if(i > max){
            max = i;
        }else if(i < min){
            min = i;
        }
    }
    //创建中间数组的大小
    int k = max - min + 1;
    int[] c = new int[k];
    //确定C数组中某个位置的值的大小
    for(int i = 0; i < a.length; i++){
        c[a[i] - min] += 1;//改进的地方，不用创建很大的中间数组了
    }
    //确定C中某项的值（包括小于和等于其小标的所有值）
    for(int i = 1; i < c.length; i++){
        c[i] = c[i] + c[i - 1];
    }
    //按存取方式取出c中的元素，放入b数组中
    for(int i = a.length - 1; i >= 0; i--){
        b[--c[a[i] - min]] = a[i];
    }
    return b;
}

3）评价：计数排序是用来排序0到100之间的数字的最好的算法，但它不适合按字母顺序排序人名。计数排序对于数据范围很大的数组，需要大量时间和内存，并不适用。

9.桶式排序

1）说明：扫描序列A，根据每个元素的值所在的区间，放入指定的桶中（顺序放置），然后对每个桶中的元素进行排序（什么排序算法都可以，比如插入排序），最后依次收集每个桶中的元素，顺序放置到输出序列中。

2）实现：

    public static void bucketSort(int[] arr){
        //确定数组中最大值和最小值
        int max = arr[0];
        int min = arr[0];
        for(int i = 0; i < arr.length; i++){
            if(max < arr[i]){
                max = arr[i];
            }else if(min > arr[i]){
                min = arr[i];
            }
        }
        //初始化桶(这里简单地用二维数组表示桶的集合，每个一维数组表示一个桶，实际上应该用链表来表示桶，因为元素的个数并不确定)
        int bucketCount = (max - min) / arr.length + 1;
        int[][] buckets = new int[bucketCount][arr.length];
        //每个桶的当前存储位置
        int[] order = new int[bucketCount];
        //把原始数组中的元素分配到各个桶中
        for(int i = 0; i < arr.length; i++){
            //k表示该数被分配到第几个桶
            int k = arr[i] / arr.length;
            buckets[k][order[k]] = arr[i];
            order[k]++;
        }
        //将各个桶中的数据排序
        for(int i = 0; i < bucketCount; i++){
            Arrays.sort(buckets[i]);
        }
        //按顺序，将一个一个桶中的元素打印出来
        for(int i = 0; i < bucketCount; i++){
            for(int j = 0; j < buckets[i].length; j++){
                if(buckets[i][j] != 0){
                    System.out.print(buckets[i][j] + " ");
                }
            }
        }
    }

这个实现方法采用数组来表示桶，并不是太合适，最好能够使用一个链表表示一个桶，这样比较灵活。这个方法采用Java的Arrays类的静态搜索方法Arrays.sort()来对每个桶中的序列排序，主要为了方便.

10.基数排序

1）说明：桶排序都只是在研究一个关键字的排序，而基数排序能够对多个关键字进行排序。基数排序分为：MSD排序和LSD排序。MSD排序：先以主关键字排序，将序列分成主关键字相同的若干堆，再按照次关键字对每一堆单独排序；LSD排序：首先按照次关键字排序，然后按照首要关键字排序，要求是排序的算法必须是稳定的，否则会取消前一次排序的结果。

2）实现：

public static void radixSort(int[] arr, int d){
    int n = 1;//表示位数，开始的时候是个位
    int k = 0;//下标，用于保存每一位的排序结果，用于下一位排序的输入
    //创建桶
    int[][] buckets = new int[10][arr.length];
    //创order数组表示当前桶的位置
    int[] order = new int[arr.length];
    while(n < d){
        //将待排序列分配到各个桶里
        for (int num : arr) {
            //表示该数应该存在第几个桶中
            int digit = (num / n) % 10;
            //order[digit]初始值为0
            buckets[digit][order[digit]] = num;
            order[digit]++;
        }
        //按顺序将桶中的序列赋值到原数组
        for(int i = 0; i < arr.length; i++){
            if(order[i] != 0){
                for(int j = 0; j < order[i]; j++){
                    arr[k] = buckets[i][j];
                    k++;
                }
            }
            //还原，便于下一次排序
            order[i] = 0;
        }
        //还原，便于下一次排序
        n *= 10;
        k = 0;
    }
}

3)评价：计数排序、桶式排序和基数排序都是非基于比较的排序算法，而其时间复杂度依赖于数据的范围，桶排序还依赖空间的开销和数据的分布。基数排序是一种对多元组排序的有效方法，具体实现要用到计数排序或桶排序。

参考文献：
三种线性排序算法 计数排序、桶排序与基数排序
排序算法-维基百科