@caoo
2021-08-13T15:02:07.000000Z
字数 4778
阅读 365
Datawhale吃瓜教程学习之(三)决策树
文章列表
决策树概述
决策树属于非线性模型,可以用于分类,也可用于回归。它是一种树形结构,可以认为是if-then规则的集合,是以实例为基础的归纳学习。基本思想是自顶向下,以信息增益(或信息增益比,基尼系数等)为度量构建一颗度量标准下降最快的树,每个内部节点代表一个属性的测试,直到叶子节点处只剩下同一类别的样本。
决策树主要算法有:ID3(Quinlan,1979,1986)、C4.5(Quinlan,1993)、CART(Breiman,1984)
几种决策树算法比较:
1、ID3:以信息增益为准则划分属性。
2、C4.5:不直接使用信息增益,而使用增益率。而且不是直接使用增益率打的候选属性。而是启发式,先从候选属性中选择信息增益高的,在选择增益率高的选择。(对取值数目小的属性有所偏好)
3、CART:使用基尼指数,选择基尼指数小的属性(基尼指数衡量随机抽取2个样本,其类别不一样的概率)
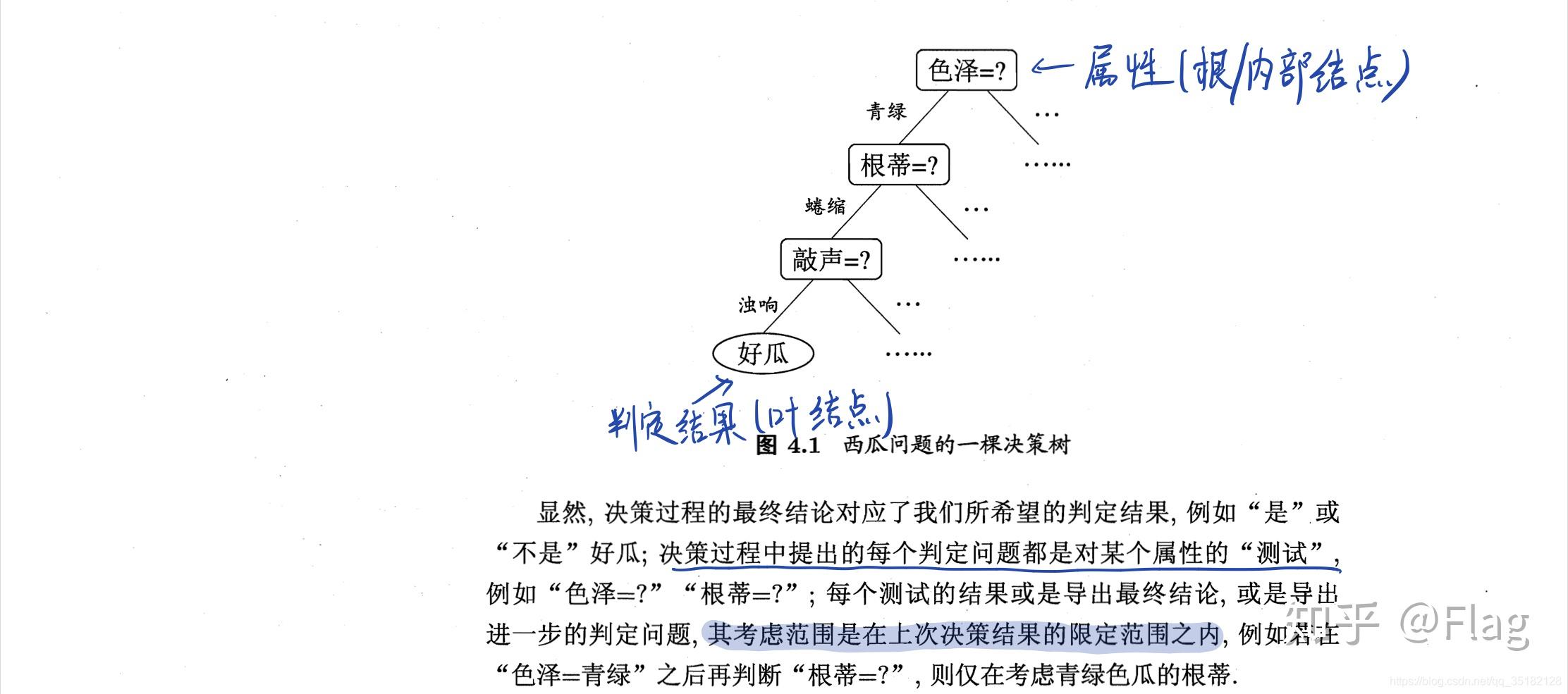
我们看看决策树是什么?
如图所示,决策树模型就是个树形结构。由结点(node)和有向边(directed edge)组成。结点分内部结点和叶结点。内部结点是一个特征,叶结点是类别。
划分选择
决策树的关键在第8行,如何选择最优划分属性,一般而言,随着划分过程不断进行,我们希望决策树的分支节点所包含的样本尽可能属于同一类别,即节点的“纯度”越来越高。
信息增益
“信息熵”是度量样本集合纯度最常用的一种指标。
信息熵
当前样本D中的第k类样本(比如好瓜、坏瓜)所占的比例为p_kpk,则D的信息熵为上面公式,值越小,纯度越高
信息增益(ID3决策树)
表示属性a的可能取值为, 信息增益越大,使用a属性来划分所获得的“纯度提升越大”,因此我们可以使用信息增益作为决策树的划分属性选择,就如第8行的, ID3决策树学习算法就是使用信息增益为准则划分属性。
增益率(C4.5决策树)
使用信息增益的缺点可能划分纯度很大,但是决策树不具有泛化能力,就是过拟合,无法对新样本进行有效的预测,信息增益准则对可能取值数目较多的属性有所偏好。C4.5决策树算法使用增益率来选择最优划分属性。
称为属性a的“固有值”,属性a的取值数目越多,值越大。增益率准则对可取值数目较少的属性有所偏好。所以C4.5决策树算法使用了一个启发式的算法:先从候选划分属性中找出信息增益高于平均水平的属性,再从中选择信息增益率最高的。
基尼指数(CART决策树)
数据集D的纯度用基尼指数表示为:
基尼指数越小,纯度越高
属性a的基尼指数为:
在候选属性集合A中,选择使得划分后基尼指数最小的属性作为最优划分属性,
如何应对过拟合?
剪枝(pruning)是决策树学习算法对应过拟合的主要手段。主要有两种剪枝方法:
剪枝处理
现在来考虑一个问题:决策树是不是形态越丰富,分支越多,越复杂,分类越准确呢?
显然是否定的。
学习算法中存在着一个需要特别注意的问题:“过拟合”。换句话说就是学习过程中过度的学习了训练集的特点,把训练集自身的一些特点当作所有样本数据都具有的一般性质,也就是学的太过了,有一些不应该继续分支的结点继续进行划分了,导致分支过多过冗余。这样子反而会降低学习算法的泛化能力。剪枝对于决策树的泛化性能的提升是显著的,有实验研究表明[Mingers,1989a],在数据带有噪声时,通过剪枝甚至可以将决策树的泛化性能提高25%
所以剪枝这一名词也因此得来,因为剪枝的目的就是剪去过多的分支!决策树剪枝的基本策略有“预剪枝”和“后剪枝”,两者的界定就是一个发生在决策树生成过程中,一个是发生在决策树生成后。
预剪枝
预剪枝的定义就是在决策树生成的过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能的提升,则停止划分,并将当前结点标记为叶子结点。
我们可以通过留出法来对泛化性能进行评估。将样本集合分为训练集和验证集。在基于前面提到的几种属性划分选择的基础上,对比划分前后的验证集的准确率来进行泛化性能的评估。如果经过划分后,验证集的准确率提高了,则认为当前结点的划分对于泛化性能的提升是有意义的,否则不计划分。
通过预剪枝,不仅可以降低过拟合的风险,同时因为限制了无意义的结点划分,在训练和测试的计算成本上也有所优化。
由以上论述,通过预剪枝可减少树的深度,故会降低决策树的时间开销;但一方面因为“贪心”的策略,会导致“欠拟合”的现象。是通过通过
后剪枝
后剪枝是发生于决策树生成完成以后,从由底至上考虑每个非叶节点,若将该结点替换为叶节点能够给决策树带来泛化性能的提升的话,则将该结点替换为叶节点。
因为后剪枝是在生成了决策树后,才开始剪枝行为,时间开销较大;但一般模型效果比预剪枝好,且不易导致“欠拟合”现象。
若属性是连续值,该怎么处理?
采用二分法(bi-partition)对连续属性进行处理。如C4.5决策树。
大致流程: 对连续属性进行离散化处理(取相邻两个值的中位点);基于某个值t进行二分类的划分,并计算该划分点的信息增益;选择信息增益最大的属性最为分裂属性。
若属性出现缺失值,该怎么处理?
先计算无缺失值时的信息增益,然后基于无缺失值的样本数/总样本数 的比例,计算总数据集的信息增益。
多变量决策树
多变量决策树(multivariate decision tree)也叫斜决策树(oblique decision tree)。
多变量决策树”的属性测试不再是单一的属性测试,而是对多个属性的线性组合进行测试。换句话说,对于分支结点的属性测试,我们不再是为每个结点寻找一个最优划分属性了,而是对每个分支结点建立一个合适的线性分类器
与“普通的决策树分类边界”相比,采用“多变量决策树”能够通过斜的划分边界取得较好的效果
决策树基本流程
决策树的一般流程
- (1) 收集数据:可以使用任何方法。
- (2) 准备数据:树构造算法只适用于标称型数据,因此数值型数据必须离散化。
- (3) 分析数据:可以使用任何方法,构造树完成之后,我们应该检查图形是否符合预期。
- (4) 训练算法:构造树的数据结构。
- (5) 测试算法:使用经验树计算错误率。
- (6) 使用算法:此步骤可以适用于任何监督学习算法,而使用决策树可以更好地理解数据
的内在含义。
这里我们提供一份完整流程代码:
决策树分类器实现Iris代码
IRIS 决策树 DecisionTreeClassifier
from sklearn.tree import DecisionTreeClassifierfrom sklearn.ensemble import AdaBoostClassifierfrom sklearn.model_selection import GridSearchCVfrom sklearn.model_selection import train_test_split#Fixing a random seedimport randomrandom.seed(42)iris = datasets.load_iris()param_grid = {"base_estimator__criterion": ["gini", "entropy"],"base_estimator__splitter": ["best", "random"],"n_estimators": [1, 2]}dtc = DecisionTreeClassifier()ada = AdaBoostClassifier(base_estimator=dtc)iris = datasets.load_iris()X = iris.data[:]y = iris.target# Split the data into training and testing setsX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)#输出数据集大小print ('原始数据集特征:',X.shape,'训练数据集特征:',X_train.shape ,'测试数据集特征:',X_test.shape)print ('原始数据集标签:',y.shape,'训练数据集标签:',y_train.shape ,'测试数据集标签:',y_test.shape)grid_search_ada = GridSearchCV(ada, param_grid=param_grid, cv=10)grid_fit = grid_search_ada.fit(X, y)# TODO: Get the estimator.best_clf = grid_fit.best_estimator_# Fit the new model.best_clf.fit(X_train, y_train)# Make predictions using the new model.best_train_predictions = best_clf.predict(X_train)best_test_predictions = best_clf.predict(X_test)print(sum(best_test_predictions == y_test)) #预测结果与真实结果比对print(metrics.classification_report(y_test,best_test_predictions))print(metrics.confusion_matrix(y_test,best_test_predictions))L1 = [n[0] for n in X_test]L2 = [n[1] for n in X_test]plt.scatter(L1,L2, c=test_predictions,marker='x')plt.title('DecisionTreeClassifier')plt.show()
总结决策树优缺点:
优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据。
缺点:可能会产生过度匹配问题。适用数据类型:数值型和标称型。
