图像处理学习

图像处理 学习笔记

什么是图像

1. 图像可以用一个定义在平面坐标上的二维函数I=f(x,y)来表示
   

   定义域(x,y)是平面坐标，
   值域I=f(x,y)是点（x,y）的亮度或彩色值

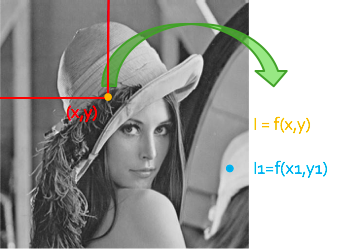
图像的数字化——把连续的感知图像转化为离散的数字形式

1. 取样

取样(Sampling):图像函数定义域(空间坐标)的数字化
分辨率:水平方向上的像素个数N和垂直方向上的像素个数M
一般而言,以左上角作为数字图像坐标的原点。

2. 量化

量化(Quantization):图像函数值域(灰度值) 的数字化
像素深度:指存储每个像素所用的位数
量化级别:可调,2,8,16...,256为常见

非统一的取样和量化

1. 非统一的取样

灰度级变化尖锐区域 => 高分辨率采样
灰度级比较平滑区域 => 低分辨率采样

2. 非统一的量化

边界附近区域 => 较少灰度级
灰度变化比较平滑的区域 => 较高灰度级 （避免或减少由于量化的太粗糙,在灰度级变化平滑的区域出现假轮廓的现象 ）

数字图像的存储：文件格式

如图像高度和宽度等信息

顺序存放的连续数据

1. 位图文件头
2. 位图信息头
3. 调色板
4. 图像数据

图像颜色空间

RGB

HIS

像素间相邻关系

4邻域

D邻域

8邻域

图像处理

马赛克

图像卷积

模糊（低通滤波）

锐化（高通滤波）

边缘检测

平移、缩放、旋转

1. 平移（offsetX, offsetY）

x` = x+offsetX
y` = y+offsetY  

2. 缩放

x` = x*scale
y` = y*scale

3. 旋转
旋转180° I (x,y)= I`(W-x, H-y)

旋转90° I (x,y)= I`(y, W-x)

旋转-90° I (x,y)= I`(H-y, x)

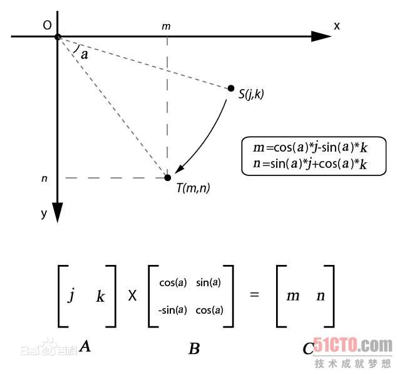
旋转矩阵

借助旋转矩阵计算图像旋转

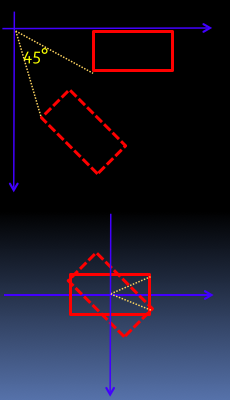
不同旋转中心点产生的不同结果

仿射变换矩阵

集成了图像的旋转和平移缩放

↓

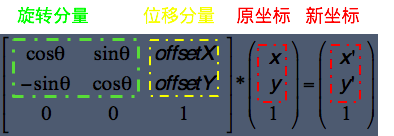
插值运算

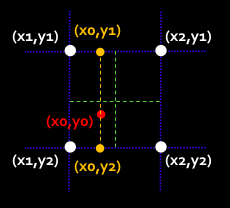
最近临插值

f(x0,y0)= I(x1, y2)

双线性插值

f(x0,y1)= I(x1, y1)+I(x2, y1)*(x0-x1)/(x2-x1)
f(x0,y2)= I(x2, y1)+I(x2, y2)*(x0-x1)/(x2-x1)
f(x0,y0)= f(x0, y1)+f(x0, y2)*(y0-y1)/(y2-y1)

鸣谢 孙腾