大叔学ML第五：逻辑回归

大叔学ML

---

基本形式

逻辑回归是最常用的分类模型，在线性回归基础之上扩展而来，是一种广义线性回归。下面举例说明什么是逻辑回归：假设我们有样本如下（是我编程生成的数据）：

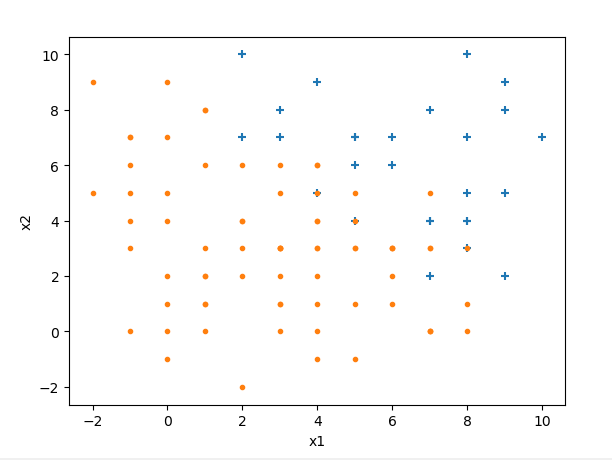
我们要做的是找到一个决策边界，把两类样本给分开，当有新数据进来时，就判断它在决策边界的哪一边。设边界线为线性函数

$$h_\theta(\vec x) = \theta_0 + \theta_1x_1 + \theta_2x_2 \tag {1}$$ 取0时的直线，如下图：

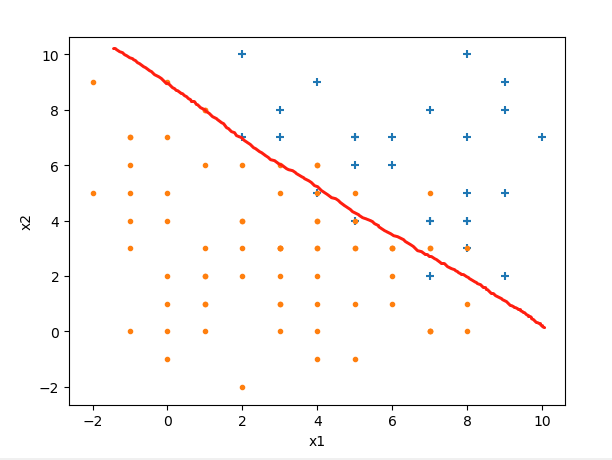
我们的目标就是根据已知的样本来确定$\vec\theta$取值。

上图中，处在边界线左边的为负例（带入（1）式结果小于0），边界线右边的为正例（带入（1）式结果大于0）。从概率的角度考虑：把一个点代入（1）式，如果为正，且越大越离边界线远，它是正例的概率就越大，直到接近1；相反，把一个点代入（1）式，如果为负，且越小离边界线越远，它是正例的概率就越小，直到接近0；此外，把一个点代入（1）式，如果结果正好等于0，那么它在边界线上，为正例和为负例的概率都是0.5。

为了用数学的方式精确表达上面的概率论述，前人找到一个好用的函数：

$$s(z) = \frac{1}{1+e^{-z}} \tag{2}$$
这个函数叫做sigmoid（sigmoid：S形状的）函数（下文用S(z)或s(z)表示sigmoid函数），样子如下：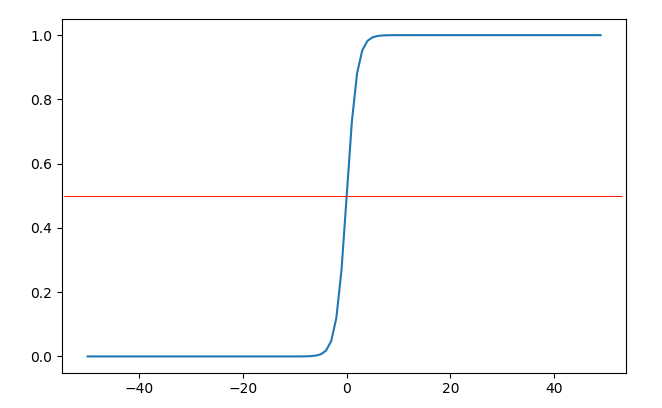

当$z=0$时，函数值为0.5，当$z > 0$时，函数取值$(0.5, 1)$；当$z < 0$时，函数取值$(0, 0.5)$，如果我们把欲判断点代入决策边界（1）式后得到的结果作为sigmoid函数的输入，那么输出就可以表示该点是正例的概率，简直完美。其实S型的函数应该还有别的，为什么前人独爱这个呢？那是因为，这个函求导比较简单，用链式法则可以非常容易算出其导数式为：

$$\frac{d}{z}s(z)=s(z)(1 - s(z)) \tag{3}$$

simgiod函数求导过程：

$$\begin{align}\frac{d}{z}s(z)&=-\frac{1}{(1+e^{-z})^2}\cdot e^{-z} \cdot -1 \\ &=\frac{e^{-z}}{(1+e^{-z})^2}\\ &=\frac{1+e^{-z}-1}{(1+e^{-z})^2}\\ &=\frac{1+e^{-z}}{(1+e^{-z})^2} - \frac{1}{(1+e^{-z})^2}\\ &=s(z) - s(z)^2\\ &=s(z)(1-s(z)) \end{align}$$
第一步用了链式法则。

代价函数

逻辑回归的代价函数可由极大似然估计法得出。我们暂且不管极大似然估计法的证明，直观地理解非常容易：如果你是一个班级的新老师，发现有个孩子考了95.5分，你肯定会认为这个孩子很可能是学霸，虽然学霸有时也会考低分，学渣有时也考高分，但是发生概率很小。更一般的叙述是：有若干事件A、B和C，已知其发生概率为分别为$P(A|\theta)$、$P(B|\theta)$和$P(C|\theta)$，如果我们观察到A、B和C已经发生了，那么我们就认为$P(ABC|\theta)$是个尽可能大的值，如果我们要求$\theta$，那么$\theta$应该是使得$P(ABC|\theta)$最大的那个值。如果A、B和C互相独立，我们所求的就是使得$P(A|\theta)P(B|\theta)P(C|\theta)$最大化的$\theta$。

设$t_\theta(\vec x)=s(h_\theta(\vec x))$已知：

$$P(Y=y) = \begin{cases} t_\theta(\vec x), &\text{如果 y = 1} \\ 1 - t_\theta(\vec x), &\text{如果 y = 0} \end{cases}$$ ，写到一起：
$$P(Y=y)=t_\theta(\vec x)^y(1-t_\theta(\vec x))^{1-y} \tag{4}$$ ，根据（4）式写出极大似然函数：
$$l(\vec\theta)=\prod_{i=1}^mt_\theta(\vec x^{(i)})^{y^{(i)}}(1-t_\theta(\vec x^{(i)}))^{1-y^{(i)}}$$ ，设代价函数 $$j(\vec\theta)=-\frac{1}{m}\ln l(\vec\theta)$$ ，最大化$l(\vec\theta)$即最小化$j(\vec\theta)$。求对数是为了方便计算，把乘法转换为加法，把幂运算转换为乘法，单调性不变；前面的负号是为了把求最大值问题转换为求最小值问题，习惯上，应用梯度下降法时都是求最小值，不然叫“梯度上升了法”了，手动滑稽。当然，使用梯度下降法的前提条件是函数是凸的，大叔懒得证明了，这个函数就是个凸函数，不管你们信不信，我反正是信了。进一步对上式化解得：
$$j(\vec\theta)=-\frac{1}{m}\sum_{i=1}^m\left[y^{(i)}\ln t_\theta(\vec x^{(i)}) + (1-y^{(i)})\ln(1-t_\theta(\vec x^{(i)}))\right] \tag{5}$$

用梯度下降法求$\vec\theta$

将（5）式对$\vec\theta$求偏导：

• $\frac{\partial}{\partial\theta_0}j(\vec\theta)=\frac{1}{m}\sum_{i=1}^m(t_\theta(\vec x^{(i)})-y^{(i)})x_0^{(i)}$
• $\frac{\partial}{\partial\theta_1}j(\vec\theta)=\frac{1}{m}\sum_{i=1}^m(t_\theta(\vec x^{(i)})-y^{(i)})x_1^{(i)}$
• $\cdots$
• $\frac{\partial}{\partial\theta_n}j(\vec\theta)=\frac{1}{m}\sum_{i=1}^m(t_\theta(\vec x^{(i)})-y^{(i)})x_n^{(i)}$

如果读者对矩阵计算非常熟悉的话，应该可以看出，上式可以写成矩阵形式，这样计算更方便：

$$\frac{\partial}{\partial\vec\theta}=\frac{1}{m}X^T(T-Y)，其中，T=\begin{pmatrix}t_\theta(\vec x^{(1)})\\ t_\theta(\vec x^{(2)})\\ \vdots \\ t_\theta(\vec x^{(m)}) \end{pmatrix}$$

对$j(\vec\theta)$求导的过程如下，多次应用链式法则即可：

$$\begin{align} \frac{\partial}{\partial\theta_n}j(\vec\theta)&=-\frac{1}{m}\sum_{i=1}^m\left[y^{(i)}\frac{1}{t_\theta(\vec x^{(i)})}t_\theta(\vec x)^\prime+(1-y^{(i)})\frac{1}{1-t_\theta(\vec x^{(i)})}t_\theta(\vec x)^\prime\right]\\ &=-\frac{1}{m}\sum_{i=1}^m\left[y^{(i)}\frac{1}{t_\theta(\vec x^{(i)})}t_\theta(\vec x^{(i)})(1-t_\theta(\vec x^{(i)}))h_\theta(\vec x)^\prime+(1-y^{(i)})\frac{1}{1-t_\theta(\vec x^{(i)})}t_\theta(\vec x^{(i)})(t_\theta(\vec x^{(i)}) - 1)h_\theta(\vec x)^\prime\right]\\ &=-\frac{1}{m}\sum_{i=1}^m\left[y^{(i)}(1-t_\theta(\vec x^{(i)}))h_\theta(\vec x)^\prime + (y^{(i)})t_\theta(\vec x^{(i)} - 1)h_\theta(\vec x)^\prime\right]\\ &=-\frac{1}{m}\sum_{i=1}^m\left[y^{(i)}(1-t_\theta(\vec x^{(i)}))x_n^{(i)} + (y^{(i)})t_\theta(\vec x^{(i)} - 1)x_n^{(i)}\right]\\ &=-\frac{1}{m}\sum_{i=1}^m(y^{(i)} - t_\theta(\vec x^{(i)}))x_n^{(i)}\\ &=\frac{1}{m}\sum_{i=1}^m(t_\theta(\vec x^{(i)}) - y^{(i)})x_n^{(i)} \end{align}$$
- 步骤1用到到了公式：$\ln x^\prime = \frac{1}{x}$
- 步骤2用到式（3）

有了偏导式后就可以编程了：

import matplotlib.pyplot as plt
import numpy as np
def sigmoid(z):
    return 1 / (1 + np.e**(-z))
def draw_samples(X, Y, sample_count):
    ''' 绘制正负例. '''
    positiveX1 = []
    positiveX2 = []
    negativeX1 = []
    negativeX2 = []
    for i in range(sample_count):
        if Y[i, 0] == 1:
            positiveX1.append(X[i, 0])
            positiveX2.append(X[i, 1])
        else:
            negativeX1.append(X[i, 0])
            negativeX2.append(X[i, 1])
    plt.scatter(positiveX1, positiveX2, marker='+')
    plt.scatter(negativeX1, negativeX2, marker='.')
def draw_border(theta):
    '''绘制边界线'''
    X = []
    Y = []
    for x in range(-2, 12):
        X.append(x)
        Y.append(-theta[0] / theta[2] - theta[1] / theta[2] * x )
    plt.plot(X, Y)
def create_samples(samples_count):
    ''' 生成样本数据'''
    X = np.empty((samples_count, 2))
    Y = np.empty((samples_count, 1))
    for i in range(samples_count):
        x1 = np.random.randint(0, 10)
        x2 = np.random.randint(0, 10)
        y = 0
        if x1 + x2 - 10 > 0:
            y =1
        X[i, 0] = x1
        X[i, 1] = x2
        Y[i, 0] = y
        noise = np.random.normal(0, 0.1, (samples_count, 2))
        X += noise
    return X, Y
def grad(X, Y, samples_count, theta):
    ''' 求代价函数在theta处的梯度. '''
    T = sigmoid(np.dot(X, theta))
    g =  np.dot(X.T, (T - Y)) / samples_count
    return g
def descend(X, Y, samples_count, theta = np.array([[1],[1],[1]]), step = 0.01, threshold = 0.05):
    ''' 梯度下降.
        Args: 
            X: 样本
            Y：样本标记
            theta：初始值
            step：步长
            threshold：阈值
        Returns:
            theta：求出来的最优theta
    '''
    g = grad(X, Y, samples_count, theta)
    norm = np.linalg.norm(g)
    while norm > threshold:
        g = grad(X, Y, samples_count, theta)
        norm = np.linalg.norm(g)
        theta = theta - g * step
        print(norm)
    return theta
samples_count = 100
X, Y = create_samples(samples_count)
MatrixOnes = np.ones((100, 1))
X_with_noes = np.hstack((MatrixOnes, X)) # 添加等于1的x0
theta = descend(X_with_noes, Y, samples_count)
plt.xlabel('$x_1$')
plt.ylabel('$x_2$')
draw_samples(X, Y, samples_count)
draw_border(theta.flatten())
plt.show()

运行结果：

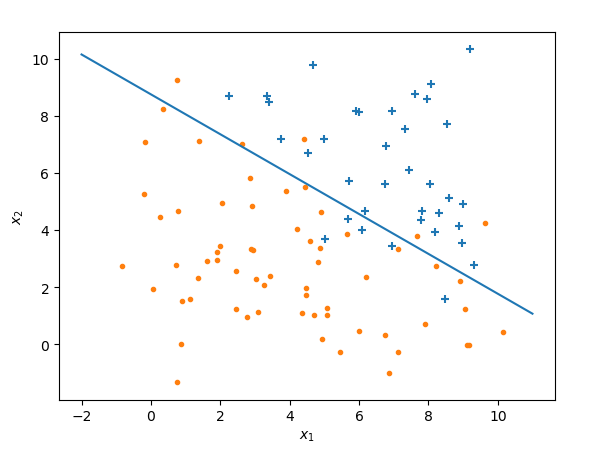
上面的代码中，我在样本矩阵中增加了一列为1的元素，这样做是为了计算方便，使得样本矩阵的列数等于欲求$\vec\theta$的行数，满足矩阵乘法的要求，加上这一列对结果没有影响，请参考大叔学ML第二：线性回归

扩展

• 和线性回归一样，逻辑回归也存在过拟合的情况，可以通过添加一范数、二范数正则化来解决
• 和线性回归一样，逻辑回归的决策边界可以是曲折的多项式，可参考大叔学ML第三：多项式回归，依葫芦画瓢来搞定决曲折的决策边界
• 和线性回归一样，逻辑回归也可以扩展到多余3维的情况，只是不可以做可视化了，代数原理是一致的
• 和线性回归不一样，逻辑回归应该没有“正规方程”，大叔昨天按照线性回归的正规方程的推导思路推导并未得出结果，查资料也未果
• 除了梯度下降法，牛顿法和拟牛顿法也是迭代下降算法，而且下降效率更好，大叔稍后将会写一篇博文介绍之

祝元旦快乐！