Logistic回归

信用评分

---

Logisitc回归在信用评分卡开发中起到核心作用。由于其特点，以及对自变量进行了证据权重转换（WOE），Logitstic回归的结果可以直接转换为一个汇总表，即所谓的标准评分卡。

基本公式

基本原理参见的我的另一篇笔记Logistic回归

通过一个简单的案例探讨其基本特征。SAS程序如下：

proc logistic data = CreditCard;
model status(event='1')=
          CustAge TmAtAddress CustIncome TmWBank
   ;
run;

该模型的参数估计：

为了计算违约概率，首先计算Z：

然后用公式计算违约概率，即：

$$Pr(Status=1) = \frac{1}{1+e^{-z}}=\frac{e^z}{1+e^z}$$
接下来更详细的检查模型并考虑模型的准确性和质量方面的问题

多重共线性

当数据是线性可分时，Logistic模型将面临两个基本问题：

• 似然函数是无线的，即没有最大值
• 模型的参数估计将是无限的。

好消息是，当proc logisitc发现疑似线性可分时，会发出一个警示并在输出结果中打印一个建议信息，说明该解是可疑的。

模型拟合统计量

Logistic回归模型的评估可以分几个阶段进行。

首先，是考虑检查似然函数值的统计量。

通过与仅包含截距项的模型进行比较，以评估将自变量引入模型的效应。
只包含截距项的似然函数值$L_1$定义如下：

$$L_1(\beta_0) = \left(\frac{n_1}{n}\right)^{n_1}\left(\frac{n_0}{n}\right)^{n_0}$$
其中，$n_0$和$n_1$分别是$y=0$和$y=1$的观测的数量。
同时，这种情况下$L_1$的对数并乘以-2：
$$-2ln(L_1(\beta_0)) = 2[n_1ln(n_1)-n_0ln(n_0)+nln(n)]$$
包含一些自变量的模型的似然函数的计算公式如下：
$$L_1 = \prod_{i=1}^n[\pi_i^{y_i}][(1-\pi_i)^{1-y_i}]$$
取对数形式并乘以-2，得到：
$$-2ln(L_1) = -2[y_iln(\pi_i)+(1-y_i)ln(1-\pi_i)]$$
类似于线性回归中多元判别系数$R^2$的基本原理，模型中包含的变量越多，包含和不包含该变量的$-2ln(L_1)$值直接的差别越大。为了惩罚包含大量自变量的模型，指定了两个标准：

• 赤池信息准则（AIC）
• 舒尔茨准则（SC），也被称作贝叶斯准则（BIC）

AIC和SC的定义都是通过增加一个条件来惩罚模型$-2ln(L_1)$中的自变量数量。他们计算截距项或整个模型的似然值如下：

$$AIC = -2ln(L_1) + 2r\\ SC = -2ln(L_1) + rln(n)$$
在这种情况下，只包含截距项和包含模型变量时准则值之间的差异越大，模型就越好。比较两个模型时，AIC和SC值较小的模型较好。需要注意的是，AIC引入了一个对模型复杂性的惩罚机制，表现为模型参数数量$r$的形式，$r$是样本规模对数的比率。因此，AIC比SC更倾向于接受复杂的模型。

最后，在Logistic回归模型的情况下，定义广义决定系数

广义决定系数被定义为包含或不包含自变量的似然函数的值。如下所示：

$$R^2 = 1 - \left[\frac{L_1(\beta_0)}{L_1(\beta)}\right]^{\frac{2}{n}}$$
只包含截距项的模型的最大值的$R^2$。即：
$$R_{max}^2 = 1 - [L_1(\beta_0)]^{\frac{2}{n}}$$
用$R_{max}^2$来对$R^2$进行修正，使其取值范围在0到1之间。定义如下：
$$\tilde{R}^2 = \frac{R^2}{R_{max}^2}$$

为了输出$R^2$和$\tilde{R}^2$的值，需要在proc logisitc的model语句中使用rsquare选项。$\tilde{R}^2$值较高的模型被认为要优于$\tilde{R}^2$值较低的模型。下列给出示例：

proc logistic data = CreditCard;
model status(event='1')=
           CustAge TmAtAddress CustIncome TmWBank
           / rsquare;
run;

输出

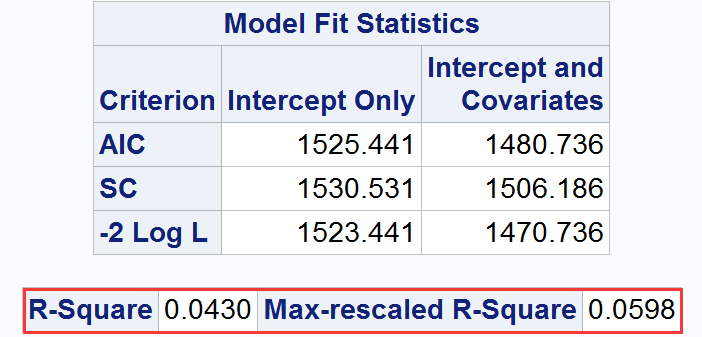
Hosmer-Lemeshow检验

Hosmer-Lemeshow检验的基本原理是将建模数据分成一定数量的段并比较每一段中实际和估计的违约数量。然后，通过计算得到一个类似卡方统计量的统计量，其显著性通过卡方分布进行评估。
该检验将建模数据分成g段，按照估计的违约概率的升序排列。
然后，计算每一段平均的估计概率，以及实际的违约数量。Hosmer-Lemeshow统计量$\chi_{HL}^2$定义为：

$$\chi_{HL}^2 = \sum_{i=1}^g\frac{(O_i-N\tilde{\pi_i})^2}{N\tilde{\pi_i}(1-\tilde{\pi_i})}$$
其中，$O_i$是第i段中违约事件的概率。$N_i$是第i段中的记录总数，$\tilde{\pi_i}$是第i段中违约的平均概率。
通过找出自由度为$g-m$的卡方分布的$p$值可以计算出$\chi_{HL}^2$的显著性，其中m是用户定义的数值。默认的m值是2。
proc logisitc将Hosmer-Lemeshow检验归类为拟合不足检验，在model语句中的选项LACKFIT<>被激活时，它将被计算并输出显示在程序结果中。如以下示例：

proc logistic data = CreditCard;
model status(event='1')=
           CustAge TmAtAddress CustIncome TmWBank
           / LACKFIT(2);
run;

输出

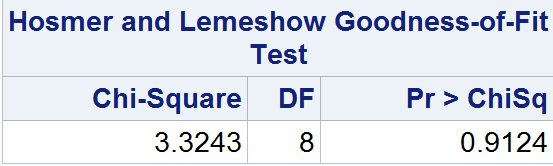
显著性检验表明，模型严重拟合不足。

全局零假设的检验

接下来，对模型质量进行的评估是对所有参数都实际为零，即$\beta = 0$的假设进行检验，该检验也被称为全局零假设。该假设的目的是检验当前的模型是否由于抽样结果偶然得到，而不是由真实的基础模型生成的数据得到。
用于检验零假设的统计量有三个：

1. 似然比统计量
2. 分数统计量
3. 沃尔德统计量

这三个检验量都默认在logistic回归模型中给出：

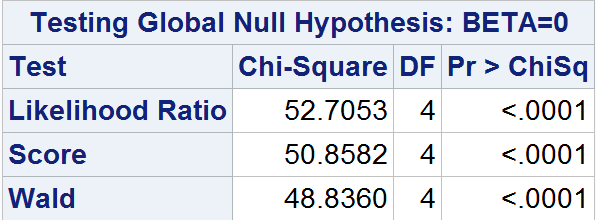
该列表表明，三个检验证明至少有一个模型参数不是0。

模型的参数解释

根据公式，logistic回归模型可以表示为：

$$log\left(\frac{p}{1-p}\right) = \beta_0+\beta_1x_1+\beta_2x_2+...+\beta_nx_n$$
考虑包含一个二元自变量的模型的情况，该自变量标记为$x$，这样，上式可以简化为：
$$log(odds) = \beta_0+\beta x$$
变量$x$取值为0或1。考虑两个观测，其中第一个$x=1$，第二个$x=0$。代入上式，得到：
$$log(odds)_1 = \beta_0 + \beta\\ log(odds)_2 = \beta_0$$
两式相减，可以得到：
$$log(odds)_1-log(odds)_2 = \beta$$
这表明模型参数$\beta$代表了违约对正常的比率的对数随着变量$x$的值从0到1的变化而递增。
这种解释是标准评分卡格式中logistic回归的基础。
继续推导得到：
$$\frac{odds_1}{odds_2} = e^{\beta}$$
等式左边就是之前定义的概率比。如果模型参数$\beta$为负值，概率比小于1，这意味着，当二元变量$x$取值为1时，将导致违约对正常的比率变小。

先验概率和权重

迄今为止，所介绍的公式都是假设代表总体的建模样本正常和违约事件的百分比相同。然而，在多数情况下，违约事件的百分比很小，所以随机抽样产生的建模数据集中只包含少量的违约事件。这种情况下，就必须使用均衡抽样的方法。
但是，如果建立logistic回归模型所用的样本不能代表总体，而是有不同的违约百分比，这意味着违约和正常的已知或先验概率不同。proc logistic提供了以下两种同样有效的解释先验概率的机制。

1. 在model语句中使用pevent选项设定模型因变量事件的先验概率的值。
2. 使用一个权重变量并用weight语句识别它。
   因为在数据描述过程中，权重变量也可以用于其他程序，所以推荐使用第二种方法。