粗分类和WOE

信用评分

---

证据权重（WOE）转换可以将logistic回归模型转变为标准评分卡格式。
引入WOE转换的目的不是为了提高模型质量，仅仅是让模型结果更直观。
可以参看这篇知乎文章深入理解WOE。

WOE的定义

下面我们拿Age(年龄)这个变量来计算相关的woe ，首先对每个level分层统计：

然后计算各分层的好坏占比:

最后通过好坏占比计算WOE

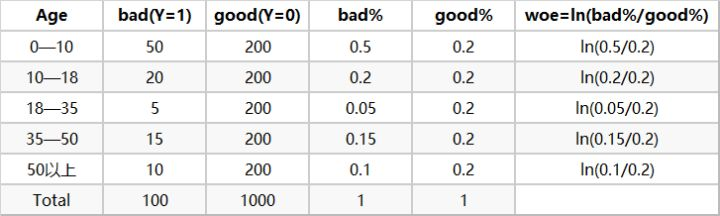
以上就是计算WOE的过程，简单易懂

每个类别的WOE定义如下：

$$WOE = ln\left[\frac{Bad\ Distribution}{Good\ Distribution}\right]$$
其中，
$$Good\ Distribution_i = \frac{Number\ of\ Good_i}{Total\ Number\ of\ Good_i}\\ Bad\ Distribution_i = \frac{Number\ of\ Bad_i}{Total\ Number\ of\ Bad_i}$$

WOE的含义

接下来的例子表明，如果用一个已经经过WOE转换的自变量对logistic回归模型进行拟合，则该变量对应的模型参数正好是1.0。

Data CC1;
  set CreditCard;
        if ResStatus='Other' then RS_WOE=-0.200487;
   else if ResStatus='Home Owner' then RS_WOE=-0.019329;
   else RS_WOE=0.095564;
run;
/* Fit a logistic regression model with 
   RS_WOE as an indpendent variable */ 
proc logistic data=CC1;
 model Status(event='1')=RS_WOE;
 run;

结果如下：

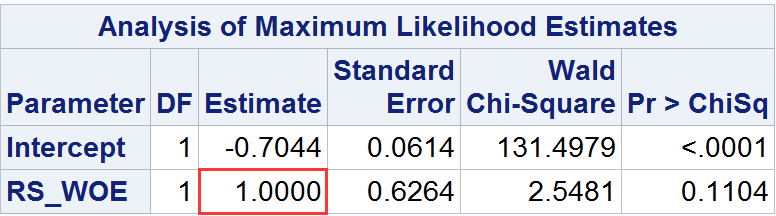
根据以上结果，可以得到如下结论：

1. 新WOE变量RS_WOE的模型参数刚好是1.0。说明WOE转换是概率比的对数的含义。
2. 可以将当前的模型表示为： $$log\left(\frac{p}{1-p}\right) = -0.7044 + 1.0*(RS\_WOE)$$ ，截距项等于违约于正常的频率之比的对数。

证据权重于标准评分卡

用公式8.5的WOE转换，可以将名义变量x的WOE重新表述为：

$$WOE(x) = \delta_1WOE_1+\delta_2WOE_2+...+\delta_rWOE_r$$
其中，$\delta_1...\delta_r$是二元虚拟变量，即对于所有的$j=1,...,r$，如果$x$的取值是第$j(x_j)$类，则$\delta_j = 1$。
因此，用一个变量证据权重的值代替该变量的各个类别，将得到的上式形式的新变量。将新转换变量用于logistic回归模型，其效果就是该模型对于该变量所有类别将生成唯一的模型参数。

下面通过一个例子来阐明上述概念及含义。

用三个名义独立变量$x_1、x_2和x_3$的logistic回归模型，模型公式可以用于违约与正常比率的形式表示如下：

$$ln(odds) = ln\left(\frac{p}{1-p}\right) = \beta_0+\beta_1x_1+\beta_2x_2+\beta_3x_3$$
需要注意的是，由于变量$x_1、x_2和x_3$的名义属性，不能直接进行拟合，因此，上式仅仅是一个概念性框架，还不是真正的模型方程。
进而，假设这些变量可以分为以下几类：

变量	分类
$x_1$	$x_{11}\ x_{12}\ x_{13}$
$x_2$	$x_{21}\ x_{22}\ x_{23}\ x_{24}$
$x_3$	$x_{31}\ x_{32}$

对这三个变量$x_1、x_2和x_3$进行WOE转换，可以得到新的转换值如下：

$$\begin{aligned} &v_1 = WOE(x_1) = \delta_{11}w_{11}+\delta_{12}w_{12}+\delta_{13}w_{13}\\ &v_2 = WOE(x_2) = \delta_{21}w_{21}+\delta_{22}w_{22}+\delta_{23}w_{23}+\delta_{24}w_{24}\\ &v_3 = WOE(x_3) = \delta_{31}w_{31}+\delta_{32}w_{32} \end{aligned}$$
用转换后的数值型变量$v_1,v_2和v_3$代替变量$x_1、x_2和x_3$，对模型进行拟合，就可以进行参数估计并得到以下模型：
$$ln(odds) = ln\left(\frac{p}{1-p}\right)=\beta_0+\beta_1v_1+\beta_2v_2+\beta_3v_3$$
将$v_1,v_2和v_3$的值代入上式得：
$$\begin{aligned} ln(odds) = ln\left(\frac{p}{1-p}\right)=&\beta_0+\beta_1(\delta_{11}w_{11}+\delta_{12}w_{12}+\delta_{13}w_{13})\\&+\beta_2(\delta_{21}w_{21}+\delta_{22}w_{22}+\delta_{23}w_{23}+\delta_{24}w_{24})\\ &+\beta_3(\delta_{31}w_{31}+\delta_{32}w_{32}) \end{aligned}$$
重新整理公式，将比率的对数表示为$\delta$的形式，可以得到下列最终的模型等式：
$$\begin{aligned} ln(odds) =&\beta_0\\ &+(\beta_1w_{11})\delta_{11}+ (\beta_1w_{12})\delta_{12}+(\beta_1w_{13})\delta_{13} \\&+(\beta_2w_{21})\delta_{21}+(\beta_2w_{22})\delta_{22}+(\beta_2w_{23})\delta_{23}+(\beta_2w_{24})\delta_{24}\\ &+(\beta_3w_{31})\delta_{31}+(\beta_3w_{32})\delta_{32} \end{aligned}$$
模型的上述表现形式就是前面所说的标准评分卡，具体解读如下：

• 首先，赋予每个申请人一个基础分支$\beta_0$
• 如果$x_1$取值为$x_{11}$，将增加$(\beta_1x_{11})$分；如果取值为$x_{12}$，将增加$(\beta_1x_{12})$分$\cdot\cdot\cdot$以此类推。
• 如果一个变量取对应类别中的值，再将每个变量圆括号中的取值对最终得分的贡献贾总。
• 总的分值，代表违约与正常比率的对数值，是所有这些分数的加总。

SAS实现

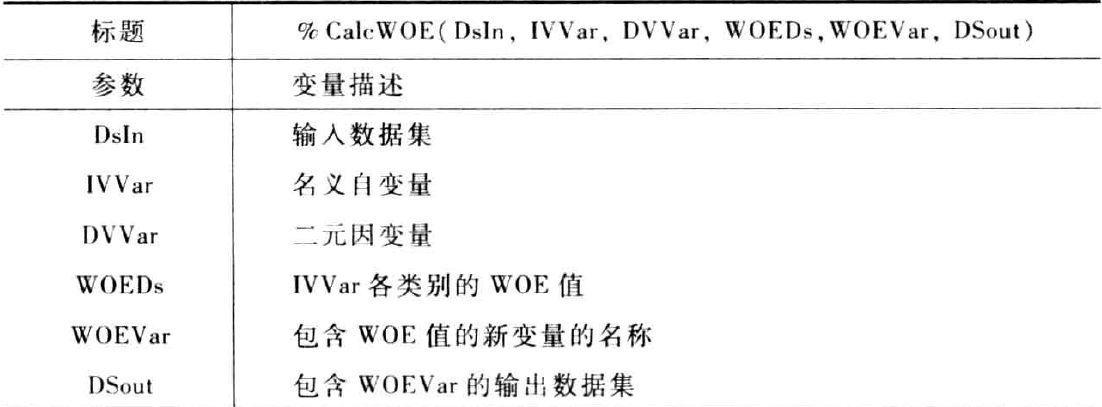
宏%CalcWOE使用一个二元因变量DVVar计算一个名义变量IVVar的证据权重，并将结果保存在数据集DSout中。宏的参数如下：

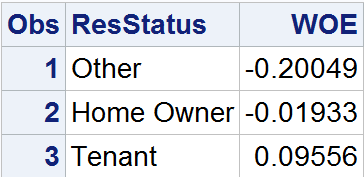
用下例程序对数据集CreditCard中的变量进行证据权重转行。

%let DsIn=CreditCard; 
%let DVVar=Status;
%let IVVar=ResStatus;
%let WOEDS=ResStatus_WOE;
%let DSout=CreditCard_WOE1; 
%let WOEVar=ResStatus_WOE;
%CalcWOE(&DsIn, &IVVar, &DVVar, &WOEDs,&woevar,&DSout);

输出如下：

连续变量的WOE

为了将WOE转换应用于连续变量，需将数值分段，以适用WOE的定义。分段方法见之前的笔记，这里选用最优分段方法。
用宏%BinContVar和%ApplyMap2可以实施最优分段。因为要针对所有候选连续自变量调用这个宏，可以引入一个新的宏按照顺序调用这两个宏。宏%BinVar实现这个功能，代码的参数如下：