Charpeter3 第三章 未定权益市场（Contingent Claims Markets）

译稿

---

　　我们的首要任务是更深入地理解表达式 $p=E(mx)$。在本章我引入一个非常简单的市场结构，未定权益（Contingent Claims）。这给我们 $p=E(mx)$ 的一个内积解释（inner product interpretation），使得大多数原理在视觉上能直观表达的。我们发现折现因子存在，且为正，同时仅从完全市场中的价格和报酬出发，定价方程为线性。我们不需要任何效用函数。下一章将说明这些性质也能建立在不完全市场的基础之上。

3.1 Contingent Claims（未定权益）

　　具体假设一个有限维的状态空间（state space），明天在所有可能的 $S$ 种自然状态 （ states of nature）中有一种会发生。将单个状态记为 $s$ 。举例来说，我们可能有 $S=2$ 且 $s=$雨天或 $s=$晴天。
　　未定权益（contingent claim ）是一种仅在明天的某一个状态 $s$ 下支付一美元（或者一单位消费品）的证券。$pc(s)$ 是这一未定权益今天的价格。我写为 $pc$ 表明其为未定权益今天的价格，$(s)$表示在哪种状态下可以追索报酬。
　　在完全市场（complete market）中，投资者能够买任何未定权益。他们不一定要交易明确的未定权益，仅需要足够的其他证券来涵盖或者构造所有未定权益。举个例子，如果可能的自然状态为 $(雨天,晴天)$ ，就可以组合未定权益，构造雨天支付2美元，晴天支付1美元的证券组合，即 $x_1=(2,1)$ 或者支付模式为 $x_2=(1,1)$ 的无风险证券组合，以此来涵盖或合成所有的未定权益或任何资产组合。
　　现在，我们在寻找折现因子，并且要点是：
　　如果有完整的未定权益，则折现因子存在，且等于未定权益价格除以概率。
　　用 $x(s)$ 表示自然状态 $s$ 下的一项资产报酬。我们将资产视为一篮子未定权益——状态1下为 $x_1$，状态2下为 $x_2$，以此类推。资产价格必须等于这些未定权益的价值：

$$p(x)=\sum_s pc(s)x(s) 　(3.1)$$ 　　我价格记为 $p(x)$ 来强调这是报酬 $x$ 的价格。在报酬明确的具体问题中，我会略去 $(x)$。我倾向将式（3.1）理解一种“开心乐园餐”原理：开心乐园餐的价格与一个汉堡、一小份炸薯条、一小杯饮料外加一个玩具的总价格相同。
　　取期望相比于对全部状态的求和更简便些。为达到此目的，将式（3.1）乘上概率并除以概率， $$p(x)=\sum_s \pi(s)({ pc(s)\over \pi(s)})x(s)$$ 其中 $\pi(s)$ 是状态 $s$ 发生的概率。接着定义 $m$ 为未定权益价格和概率的比率， $$m(s)={pc(s)\over \pi(s)}$$ 现在我们可以将该等式写为期望形式， $$p(x)=\sum_s \pi(s)m(s)x(s)=E(mx)$$
　　因此，在完全市场中，随机折现因子$m$存在，且为一系列按概率加权的未定权益价格。由于这一解释，折现因子和概率的结合有时被称为状态—价格密度（state-price density）。
　　乘以并处以概率的处理在有限状态的环境下看起来非常不自然。一般的，我们假定空间 $\Omega$ 中自然状态 $\omega$ 能够取连续（不可列无穷）的值。这种情况下，求和变为积分，同时我们必须用某种方法求积分区间为 $\Omega$ 的积分。因此，用概率近似物对未定权益价格加权是不可避免的。
　　

3.2 Risk-Neutral Probabilities风险中性概率

　　另一常见的变型引出了“风险中性”概率。定义

$$\pi^*(s)\equiv R^fm(s)\pi(s)=R^fpc(s)$$ 其中 $$R^f={1\over {\sum pc(s)}}={1\over E(m)}$$ 其中$\pi^*(s)$为正，小于等于1且和为1,所以其为合理的概率集合。现在我们重新将资产定价方程写为： $$p(x)=\sum pc(s)x(s)={{1\over R^f}\sum\pi^*(s)x(s)}={E^*(x)\over R^f}$$ 我用符号 $E^*$ 来提示我们期望使用了风险中性概率 $\pi^*$ 代替了实际的概率 $\pi$ 。
　　因此，我们可以认为资产定价是如果所有的代理都是风险中性的，但是却用概率 $\pi^*$ 代替了概率 $\pi$ 。概率 $\pi^*$ 给了平均边际效用高于平均 $m$ 的 状态更大的权重。
　　这个思想中有着非常深刻的内涵：风险厌恶相当于更关注于不景气的状态，与它们发生的实际概率相关。主观上认为负面事件——比如坠机——的概率高的人并非持有非理性的预期，他们只是给出风险中性概率或者乘积$m\times \pi$。这个乘积是所有重要的决策信息的结果：要么关注有高概率发生的偶然事件要么关注虽不太可能但有毁灭性后果的偶然事件。
　　从实际概率到风险中性概率的转换通过下式给出：
　　 $$\pi^*={m(s)\over E(m)}\pi(s)$$ 我们也可以认为折现因子 $m$ 是从实际概率 $\pi$ 到主观概率 $\pi^*$ 的导数或测度转换。资产定价的风险中性概率表达非常常见。尤其在衍生品定价中，其中结果独立于风险调整。
　　风险中性表达式在连续时间扩散过程尤为受欢迎，因为我们可以撇开协方差，仅仅调整均值。在离散时间里，改变概率同时改变一阶矩和二阶矩。假设我们从价格和折现因子的过程开始 $${dp\over p}=\mu^pdt+\sigma^pdz$$ $${d\Lambda\over \Lambda}=\mu^\Lambda dt+\sigma^\Lambda dz$$
并假设折现因子为确定资产价格， $$E_t({dp\over p})+{D\over p}dt-r^fdt=-E_t({d\Lambda \over \Lambda}{dp\over p})$$ $$\mu^p+{D\over p}-r^f=-\sigma^\Lambda \sigma^p$$
　　在“风险中性测度”中我们将每个资产价格过程的偏移程度增加了它与折现因子的协方差，并将写出风险中性折现因子， $${dp\over p}=(\mu^p+\sigma^p\sigma^\Lambda)dt+\sigma^pdz=\mu^{p*}dt+\sigma^pdz$$ $${d\Lambda\over \Lambda}=\mu^\Lambda dt$$
　　在一系列新概率下，我们可以写出风险中性定价方程 $$E^*_t({dp\over p})+{D\over p}dt-r^fdt=0$$ 当 $E^*_t({dp\over p})=\mu^{p*}dt$。与之前相同， $$\mu^p+\sigma^p\sigma^\Lambda+{D\over p}-r^f=0$$

3.3 Investors Again（再次讨论投资者）

　　尽管本章着眼于没有效用函数的情况，但在未定权益内容里再次考察投资者的一阶条件还是值得的。假设投资者最初拥有财富 $y$ 和依赖于状态（ state-contingent）的收入$y(s)$。他可能在第二期针对每种可能状态购买未定权益。那么他的问题就是：

$$max_{c,c(s)}　 u(c)+\sum_s\beta\pi(s)u[c(s)]　s.t.c+\sum pc(s)c(s)=y+\sum_spc(s)y(s)$$ 在预算约束中引入一个拉格朗日乘子 $\lambda$，一阶条件为 $$u'(c)=\lambda$$ $$\beta\pi(s)u'[c(s)]=\lambda pc(s)$$ 消去拉格朗日乘子， $$pc(s)=\beta\pi(s){u'[c(s)]\over u'(c)}$$ 或 $$m(s)={pc(s)\over \pi(s)}=\beta {u'[c(s)]\over u'(c)}$$ 外加$p=E(mx)$，我们再次得到了基于消费的模型。
　　投资者的一阶条件表明明天的各状态之间的边际替代率等于相应的价格比率， $${m(s_1)\over m(s_2)}={u'[c(s)]\over u'[c(s_2)]}$$ $m(s_1)\over m(s_2)$ 给出了投资者会通过买卖未定权益放弃状态2下的消费去换取状态1的消费的比率。 $u'[c(s_1)]\over u'[c(s_2)]$ 给出了投资者愿意做出替代的比率。最优状态下，边际替代率应该等于价格比率。
　　我们已知折现因子 $m$是日期依赖型并且是状态依赖型的商品之间边际替代率。这就是为何它，如同 $c(s)$ 一样，是随机变量的原因。同样，概率加权的未定权益价格给出了边际效用，尽管在上文这样做显得不太自然。
　　
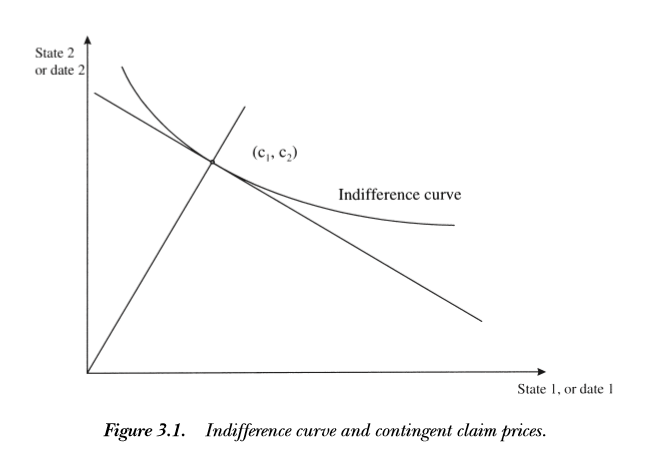
　　图3.1给出了这种定价方法背后的经济状况。我们观察投资者对日期依赖型或者状态依赖型的消费的选择。一旦我们知道他的效用函数，我们能够根据效用函数的导数计算出未定权益价格，该价格一定能引到所观察到的消费选择。
　　相应的概率为投资者主观上认为的不同状态的概率。资产价格毕竟根据投资者对资产的需求确定，这些需求根据投资者对未来各种事件的主观估计来确定。我们经常假定理性的预期，也就是主观概率等于客观频率。但是这并非是一个我们总想作出的额外假设。

3.4 Risk Sharing（风险共担）

　　我们得到任何投资者的边际替代率等于未定权益价格比率的推论。但是价格对于所有投资者都是相同的，因此，对于所有投资者边际效用增长应该相同，

$$\beta^i{u'(c^i_{t+1})\over u'(c^i_t)}=\beta^j{u'(c^j_{t+1})\over u'(c^j_t)} (3.2)$$
其中$i$与$j$指不同的投资者。如果投资者拥有同样的位似效用函数（homothetic utility function）（例如幂效用函数），那么消费本身也一致， $${c^i_{t+1}\over c^i_t}={c^j_{t+1}\over c^j_t}$$ 更一般的，个人之间的对消费的冲击也完全相互关联。
　　这种预测如此激进以至于在刚开始很容易误读这个预测。这个预测并不表明期望消费增长是相等的，而表明消费增长是相等的。如果你的消费增长10%，你的消费也恰恰增长10%，其他每个人也一样。在完全的未定权益市场，所有的投资者分担所有的风险，所以冲击来临时，所有人平等地承担冲击（在保险赔付之后）。这并非意味着消费水平是一样的——这是风险分担，不是平均主义。更富有的人有更高的消费水平，但是不论贫富平等地共担风险。
　　风险分担帕累托最优的。假设希望在既定可利用的资源条件下是所有人的效用最大化。举例来说，有两个投资者$i$和$j$，他将最大化 $$max \lambda_iE\sum_t\beta^iu(c_t^i)+\lambda_jE\sum_t\beta^ju(c_t^j) s.t. c_t^i+c_t^j=c_t^a$$ 其中$c^a$为全部可利用的总量，$\lambda_i$和$\lambda_j$是计划者主观上关于$i$和$j$的相关权重。这个问题的一阶条件为 $$\lambda_iu'(c_t^i)=\lambda_ju'(c_t^j)$$ 因此
　　这个简单的事实 首先，它表明为何总的冲击在风险价格中起作用。任何特定的收入风险应该被平等地分担，所以它的$1/N$称为了一个总的冲击。决定价格的随机折现因子$m$不再被实际的特定风险影响。仅仅总冲击起作用的思想很大程度上在非完全市场中也同样伴随我们。
　　显然，真实的经济至少目前还不是完全市场或者风险充分分担的——个人的消费并不一致地变动。然而，这一现象很大程度上告诉我们证券市场的功能所在。证券市场——状态未定权益——通过允许人们分摊一部分风险来缩小个人消费之间的差距。另外，使风险得到更好地分担是金融创新背后的驱动力。很多成功的新证券可以被视为更广泛地分担风险的工具。
　　

3.5 State Diagram and Price Function （状态图形和价格函数）

　　试将未定权益价格$pc$和资产报酬$x$视为属于$R^S$的向量，其中每个元素给出相对应状态下的价格或者报酬，

$$pc=[pc(1),pc(2)]...pc(s)]'$$ $$x=[x(1),x(2)...x(s)]'$$ 图3.2是这些向量的图形，接着，我将推导出图3.2的几何结构。
　　未定权益价格向量$pc$落于第一象限。我们在3.3节已经知道$m(s)=u'[c(s)]/u'(c)$。现在，边际效用应该始终为正（人们总是想要更多），所以边际替代率和折现因子始终非负，$m>0$且$pc>0$。不要忘了，$m$和$pc$是向量，或者随机变量。因此，$m>0$意味着在每个自然状态下实现的$m$都为正，或者等价地说向量$m$的每个要素都为正。
　　在跟定价格下的一系列报酬落于一个与未定权益向量正交的平面。我们前文推断资产报酬$x$的价格必须有它的未定权益价值给出（式（3.1））， $$p(x)=\sum_spc(s)x(s) (3.3)$$ 将$pc$和$x$变为向量，这意味着价格由未定权益价格和报酬内积给出。
　　如果两个向量是正交的——若 ——那么他们的内积为零。所以，这一系列零价格报酬必须落在与未定权益价格向量正交的平面上，正如图3.2显示的那样。
　　更一般地，$pc$与$x$两向量的内积等于$x$在$pc$方向上的模与$pc$模的乘积。用$\cdot$来表示内积，则 $$p(x)=\sum_spc(s)x(s)=pc\cdot x=|pc|\times |x|\times cos(\theta)$$ 其中$|x|$表示向量的长度，$\theta$为向量$pc$与$x$之间的角度。由于所有在平面（比如图3.2中的价格平面）上且与$pc$垂直的报酬在$pc$方向上有相同的映射，它们必须和$pc$有相同的内积以及相同的价格。（严格地讲，只有$price=0$与pc正交，由于没有更好的表述，我称非零价格平面“垂直”于$pc$）当向量为有限维时，$pc'x$是常用语记内积的主要符号，这个符号并不能很好地扩展到无限维向量空间。符号$\langle pc|x\rangle$也常常用来记内积。
　　常量价格平面线性移动，原点$x=0$处的价格为零.如果报酬$y=2x$，那么它的价格是$x$的价格的两倍， $$p(y)=\sum_spc(s)y(s)=2p(x)$$ 相似的，零报酬必然价格为零。
　　我们将$p(x)$视为定价函数，是一张从$x$坐落的状态空间（本例中的$R^s$）或者报酬空间到这条实线的地图。我们已将从定义（3.3）得到$p(x)$是线性函数的推论，即 $$p(ax+by)=ap(x)+bp(y)$$ 图3.2中的常量价格线当然正好是从$R^s$到$R$的线性函数中预期的。（可以在$z$轴上画出价格，那么价格函数将会是过原点且斜向上 的平面）
　　图3.2也包括了第一种状态下未定权益的报酬。该报酬在第一种状态时为1且在其他状态下为0，因此落在坐标轴上。价格=1单位报酬面为资产收益面；价格=0报酬面为资产超额收益面。一单位无风险报酬（无风险纯折现债券的报酬）落在图3.2中的点$(1,1)$上；无风险收益落在$45^\circ$线（所有状态报酬相等）与价格=1的平面（所有一系列收益）的交点上。

$m$代替$pc$的几何

　　图3.2的几何解释通过用折现因子$m$代替$pc$时引出。我们可定义随机变量$x$和$y$之间的内积为

$$x\cdot y=E(xy)$$ 并保留所有内积的数学特性。出于这个原因，使$E(xy)=0$的随机变量常被称为“正交”。
　　这种语言可能与线性回归。当我们做$y$对$x$的回归， $$y=b'x+\varepsilon$$ 我们通过使方差或者说残差$\varepsilon$的规模最小来找到“最接近”$y$的$x$的线性组合。我们通过使残差与右边的变量“正交”$E(x\varepsilon)=0$。$y$在$x$方向上的映射定义为固定值，$proj(y|x)=b'x=E(xx')^{-1}E(yx')x$。这一思想由与右边变量$x$所定义的平面相垂直的残差向量$\varepsilon$刻画。因此，当内积由二阶矩定义，“将$y$映射到$x$上”的操作是一次回归。（如果$x$不包含常量，你不要在回归中添加一个常量）
　　如果我们将到无限维的状态空，间图3.2的几何学的解释也是有效的 ，如果我们将随机变量赋予连续的值。区别于向量，其为$R^s$到$R$的函数，随即变量是$\Omega$到$R$的函数。尽管如此，我们仍然可以将它们视为向量。$R^s$的对应一个希伯特空间$L^2$，用来记由从$\Omega$到实线的二次积分函数的线性组合生成的空间，或者是带有限二阶矩随机变量的空间。我们仍可以将两个元素的内积定义为$x\cdot y=E(xy)$，且$p(x)=E(mx)$仍然可以被解释为“$m$垂直于常量价格平面”。证明该内容的原理稍有点困难。你不能说类似于“我们可以引出一条垂直于任何平面的直线”的话，这种事必须能够被证明。有时候，有限维会将你引入误区，所以证明其正确很重要，牢记有限维的图形。Hansen和Richard（1987）是非常好的关于希伯特空间机制的参考。