splay

DS

终于还是把目光放在 LCT 上面了，那要学LCT这东西也是必须的了

本文学习自yyb大佬的博客，因为大家说yyb是splay第一人，所以我觉得按他的写法肯定死不了

树旋转

一上来就感觉到yyb大佬的写法确实是很厉害的，以前不愿意选splay一个很大的原因就是感觉旋转分讨很麻烦的说，然后今天看到了yyb的奇妙强势写法

单旋

先考虑三个点： $x$ ，$y=fa[x]$，$z=fa[y]$

我们不妨考虑现在想要把 $x$ 旋转到 $y$ 的位置但是不破坏BST的基本性质

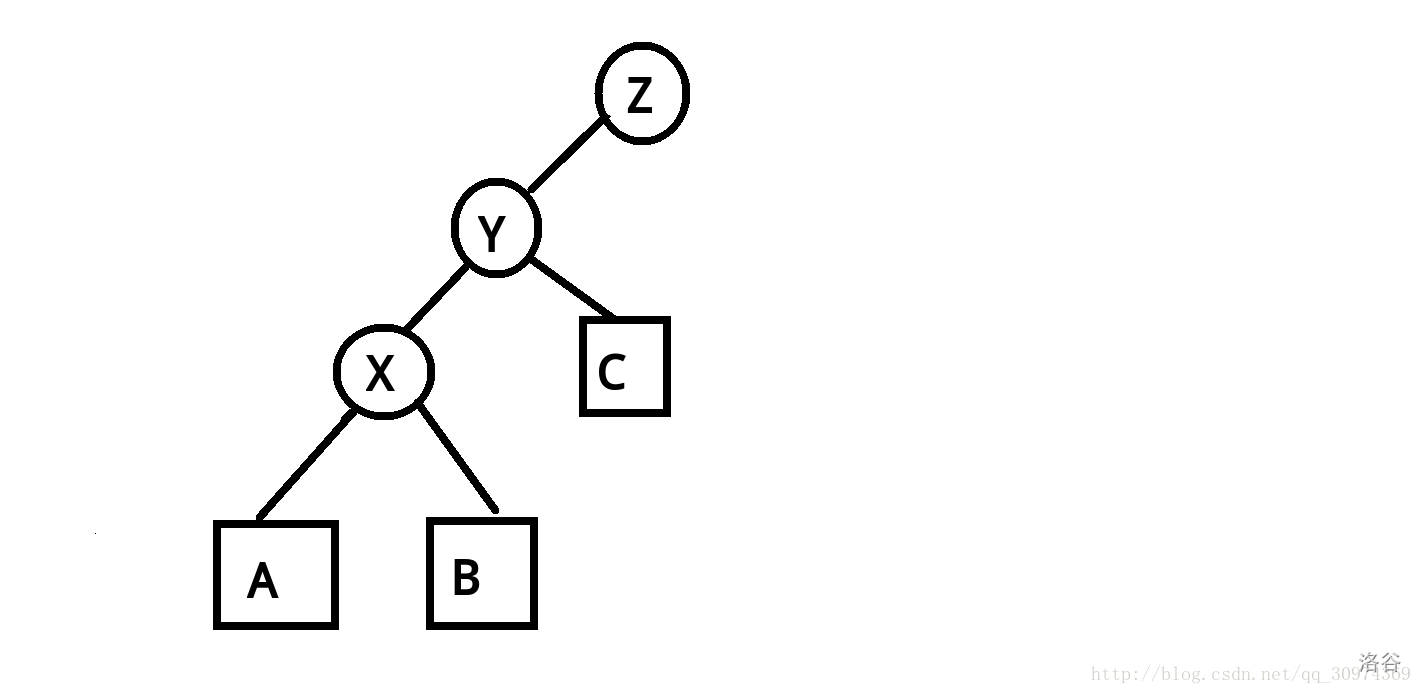
以这种情况为例

首先自然是 $x$ 要跑到 $y$ 那里去，其次由于 $x$ 是 $y$ 的左儿子所以现在 $y$ 应该是 $x$ 的右儿子，$y$ 的左儿子空出来了自然就拿 $x$ 自己本来的右儿子补上，可以发现这样是对的

找一下规律推广，就是：

1. $X$ 变到原来 $Y$ 的位置
2. $Y$ 变成了 $X$ 原来在 $Y$ 的 相反的那个儿子
3. $Y$ 顶上 $X$ 的与 $X$ 原来位置相对的那个儿子，并把 $Y$ 自己空缺的那个儿子补上

bool isd(int x){//x是他父亲的哪边儿子
    return tr[tr[x].fa].ch[1]==x;
}
void pushup(int x){
    tr[x].siz=tr[tr[x].ch[0]].siz+tr[tr[x].ch[1]].siz+tr[x].cnt;
}
void rotate(int x){
    int y=tr[x].fa,z=tr[y].fa;
    int k=isd(x);
    tr[x].fa=z;
    tr[z].ch[isd(y)]=x;
    tr[y].ch[k]=tr[x].ch[k^1];
    tr[tr[x].ch[k^1]].fa=y;
    tr[y].fa=x;
    tr[x].ch[k^1]=y;
    pushup(y),pushup(x);
}

双旋

有一个问题，我们可以手动试一下，假如我们希望把 $x$ 旋转到根结点，如果一直单旋会不会有什么问题呢

假设你已经试完了，我们会注意到这个时候树的深度并没有变化，这就意味着这个平衡了个寂寞

假设我们先要把 $x$ 旋转到 $z$ （$xyz$ 没特别说明都保持上文定义）

这个时候有两种情况：$isd(x)=isd(y)$ 和 $isd(x)\neq isd(y)$

前者我们称为同构调整，后者称为异构

对于同构，我们需要的操作是先旋转 $y$ 再旋转 $x$

异构则是 $x$ 旋转两次

原因手模即可，什么你不理解，那也没事记着就完了其实我也不理解，也许跟势能分析有关吧

于是我们可以写一个及其简单的splay操作

void splay(int x,int F){//把x旋转到F 的儿子
    while(tr[x].fa!=F){
        int y=tr[x].fa,z=tr[y].fa;
        if(z!=F)
            (isd(x)^isd(y))?rotate(x):rotate(y);
        rotate(x);
    }
    if(!F) rot=x;
}

find

查找值为 $x$ 的元素并且把 $x$ 的点扔到根

void find(int x){//找到x并旋转到根
    int u=rot;
    if(!u) return;
    while(tr[u].ch[x>tr[u].val] and x!=tr[u].val) 
        u=tr[u].ch[x>tr[u].val];
    splay(u,0);
}

insert

类似于find直接去找这个点，然后看存不存在这个数，如果存在加次数，不存在就直接就建点

这里吐槽一下yyb给的实现里前面的代码忘记pushup了（而且他文字部分说了要pushup）

void ins(int x){
    int u=rot,ff=0;
    while(u and tr[u].val!=x) ff=u,u=tr[u].ch[x>tr[u].val];
    if(u) tr[u].cnt++;
    else{
        u=++idx;
        if(ff) tr[ff].ch[x>tr[ff].val]=u;
        tr[u]={0,0,ff,1,1,x}; 
    }
    splay(u);
}

前驱后继

实现合在一起， $f=0$ 是前驱 $1$ 是后继，原理很简单把 $x$ find出来，先判断他自己是不是，然后就是小于他的最大的和大于的最小的

int nxt(int x,bool f){
    find(x);
    int u=rot;
    if(tr[u].val>x and f) return u;
    if(tr[u].val<x and !f) return u;
    u=tr[u].ch[f];
    while(tr[u].ch[f^1]) u=tr[u].ch[f^1];
    return u;
}

rank

直接find查左子树大小即可

但是注意到find找不到这个点的时候上来这个点可能是 $x$ 的前驱，这个时候就需要把这个点自己删掉，此处yyb在板子题的代码已经被hack过不了了

int rk(int x){
    find(x);
    return tr[tr[rot].ch[0]].siz+(tr[rot].val<x)*tr[rot].cnt;
}

kth

常规的平衡树

int kth(int k){
    int u=rot;
    if(tr[u].siz<k) return -inf;
    while(1){
        if(tr[tr[u].ch[0]].siz+tr[u].cnt<k)
            k-=tr[tr[u].ch[0]].siz+tr[u].cnt,u=tr[u].ch[1];
        else if(tr[tr[u].ch[0]].siz>=k) u=tr[u].ch[0];
        else return tr[u].val;
    }
}

del

可以想象，比一个数的前驱大、后继小的数只有这个数本人

于是这样搞一下就可以把这个数的点单独搞出来，后续类似

void del(int x){
    int a=nxt(x,0),b=nxt(x,1);
    splay(a),splay(b,a);
    int u=tr[b].ch[0];
    if(tr[u].cnt>1) tr[u].cnt--,splay(u);
    else tr[b].ch[0]=0,pushup(b),pushup(a);
}

我宣布我是splay的狗了！因为我splay跑的比我fhq快！

文艺区间操作

我们考虑用kth找出 $L-1$ 的区间和 $R+1$ 的区间，把 $L-1$ 转到根 $R+1$ 转到 $L-1$ 的右儿子，这样 $R+1$ 的左子树就是 $[L,R]$