exercise 08

problem 3.31

---

正文

We consider a problem of a ball moving without friction on a perfect billiard table.Between collisions the velocity is constant so we have

$$\frac{dx}{dt}=v_x$$ $$\frac{dy}{dt}=v_y$$ After locatingthe collision point,We must next obtain the unit vector normal to the wall at the point of collision,$\hat{n}$.It is then useful to calculate the components of $\hat{v_i}$parallel and perpendicular to the wall.These are just $$\vec{v}_{i,\bot}=(\vec{v}_i\cdot\hat{n})\hat{n}$$ $$\vec{v}_{i,||}=\vec{v}_i-\vec{v}_{i,\bot}$$ Hence,the velocity after reflection from the wall is $$\vec{v}_{f,\bot}=-v_{i,\bot}$$ $$\vec{v}_{f,||}=v_{i,||}$$

结果

1.for circle boundary:

import matplotlib.pyplot as plt
import numpy as np
import math
class tabel:
    def__init__(self,x_0=0.2,y_0=0,vx_0=-0.2,vy_0=-0.5,dt_1=0.001,total_time=1000):
        self.x=[x_0]
        self.y=[y_0]
        self.vx=[vx_0]
        self.vy=[vy_0]
        self.dt=dt_1
        self.time=total_time
        self.t=[0]
    def calculate(self):
        for i in range(int(self.time/self.dt)):
            self.x.append(self.x[i]+self.vx[i]*self.dt)
            self.y.append(self.y[i]+self.vy[i]*self.dt)
            self.vx.append(self.vx[i])
            self.vy.append(self.vy[i])
            if ((self.x[i+1]**2+self.y[i+1]**2>1):
                X=(self.x[i]+self.x[i+1])/2
                Y=(self.y[i]+self.y[i+1])/2
                x1=X/(X**2+Y**2)**0.5
                y1=Y/(X**2+Y**2)**0.5
                self.vx[i+1]=(1-2*x1**2)*self.vx[i]-2*x1*y1*self.vy[i]
                self.vy[i+1]=(1-2*y1**2)*self.vy[i]-2*x1*y1*self.vx[i]
                if X**2+Y**2>1:
                    self.x[i+1]=X
                    self.y[i+1]=Y
                    continue
                else:
                    self.x[i]=X
                    self.y[i]=Y
                    continue
        x_1=[-1]
        y_1=[0]
        x_2=[-1]
        y_2=[0]
        dx=0.0001
    def bound(self):
        for k in range(20000):
            x_1.append(x_1[k]+dx)
            y_1.append((1-x_1[k+1]**2)**0.5)
            x_2.append(x_2[k]+dx)
            y_2.append(-(1-x_2[k+1]**2)**0.5)
    def show_results(self):
        plt.plot(self.x,self.y,'--',label='trajectory')
        plt.plot(x_1,y_1,'--',label='bound')
        plt.plot(x_2,y_2,'--',label='bound')
        plt.xlabel(u'x')
        plt.ylabel(u'y')
a=tabel()
a.calculate()
a.show_results()
b=tabel
b.bound()
b.show_results()
plt.show()

the results:for t=50,100,1000



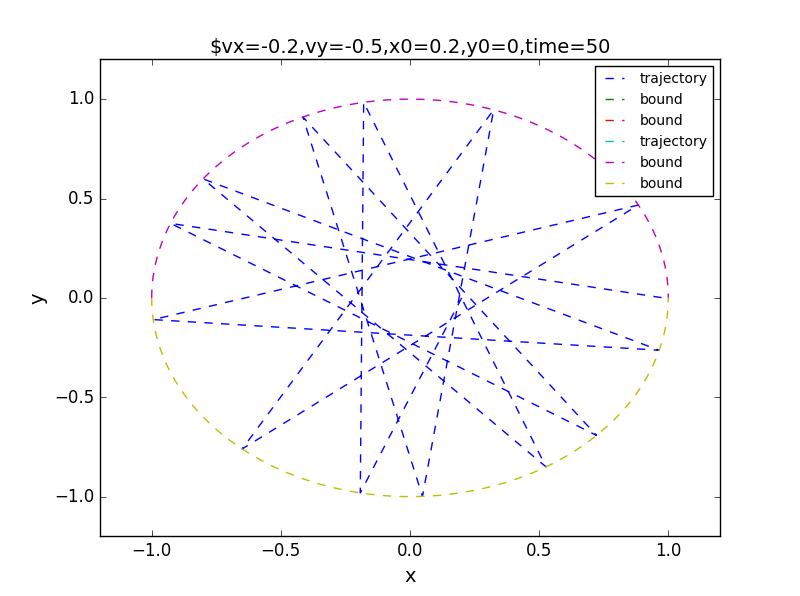
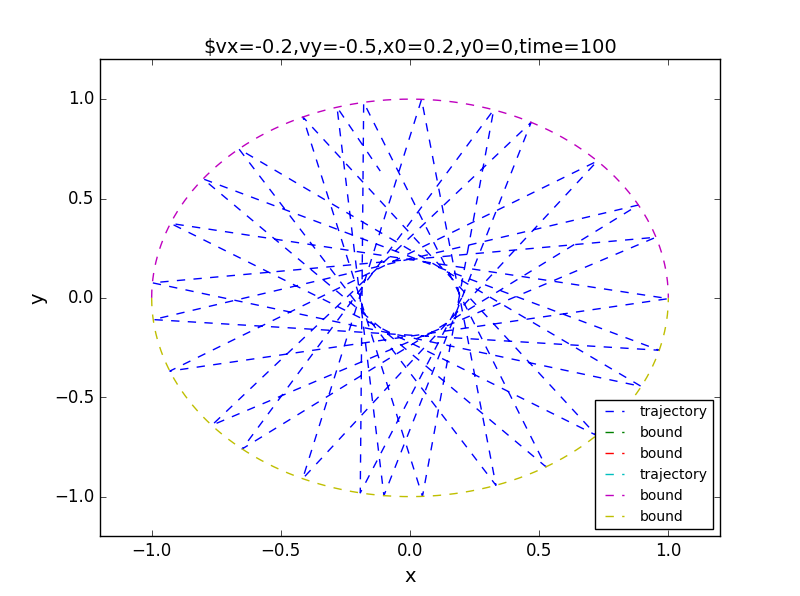
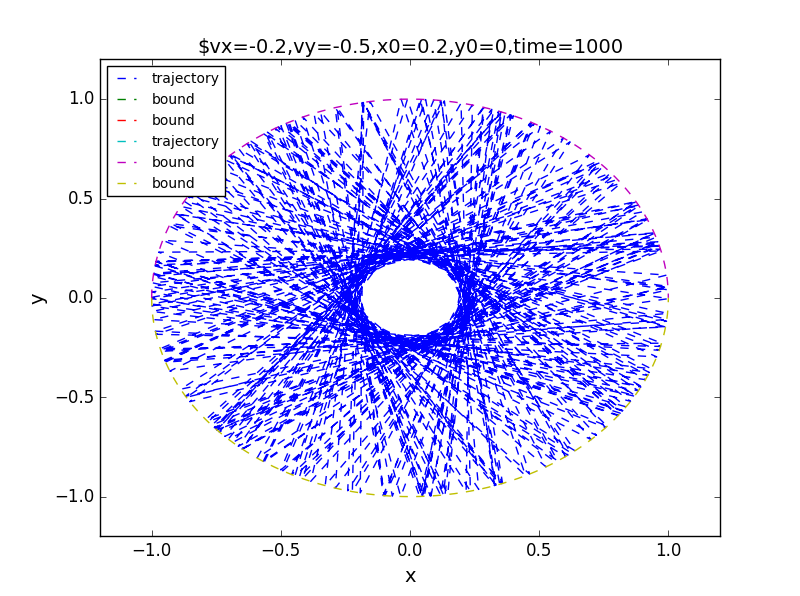
*斜体文本*the corresponding phase:

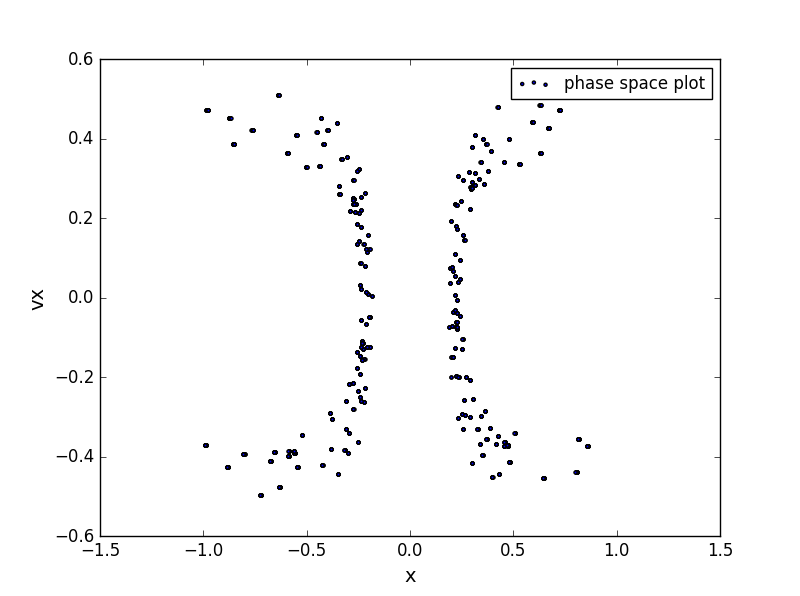
2.elliptical tabel:

the equation is

$$y^2+\frac{x^2}{4}=1$$
the code which need to change:

if ((self.x[i+1]**2/4+self.y[I+1]**2)>1):
    X=(self.x[i]+self.x[i+1])/2
    Y=(self.y[i]+self.y[i+1])/2
    x1=(X/2)/(X**2/4+Y**2)**0.5
    x2=Y/(X**2/4+Y**2)**0.5
    self.vx[i+1]=(1-2*x1**2)*self.vx[i]-2*x1*y1*self.vy[i]
    self.vy[i+1]=(1-2*y1**2)*self.vy[i]-2*x1*y1*self.vx[i]

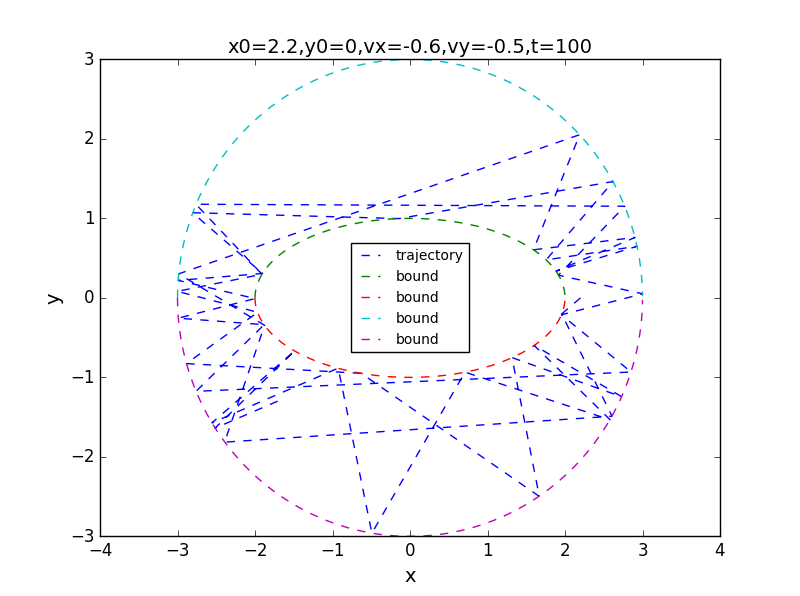
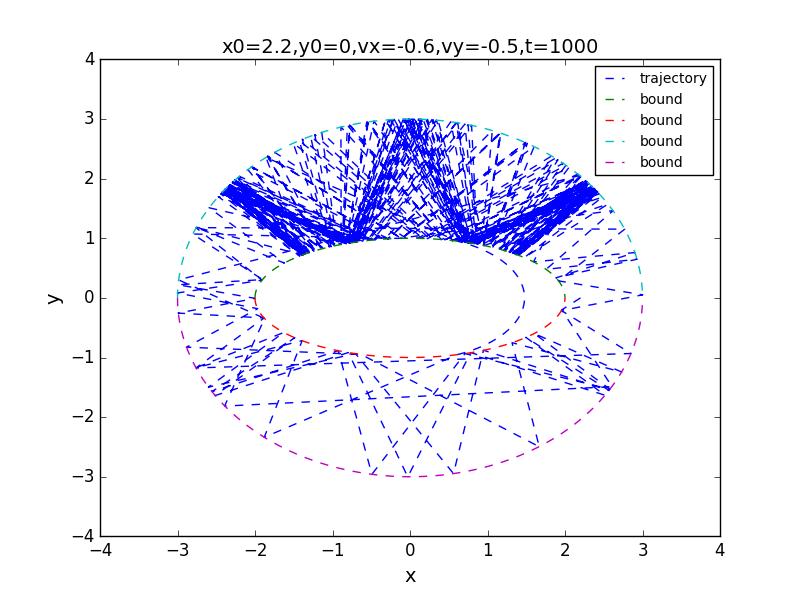
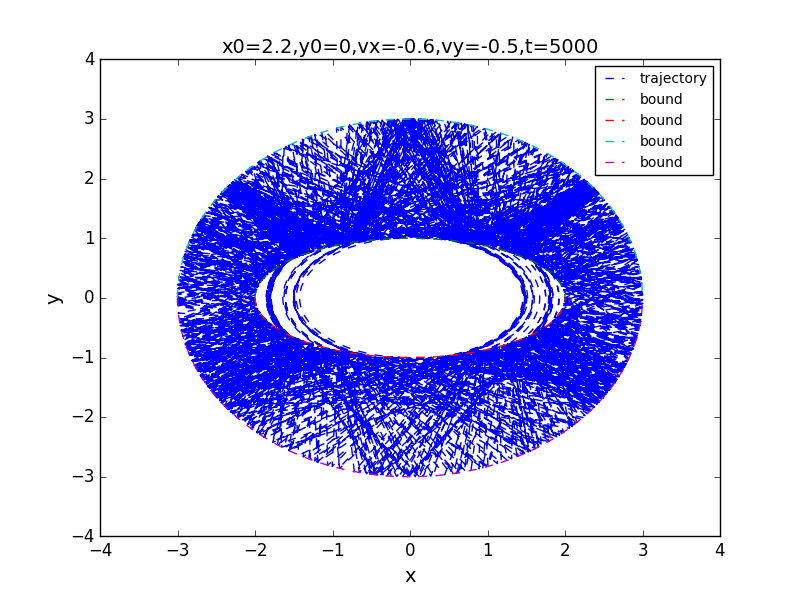
for t=100,1000,7000:



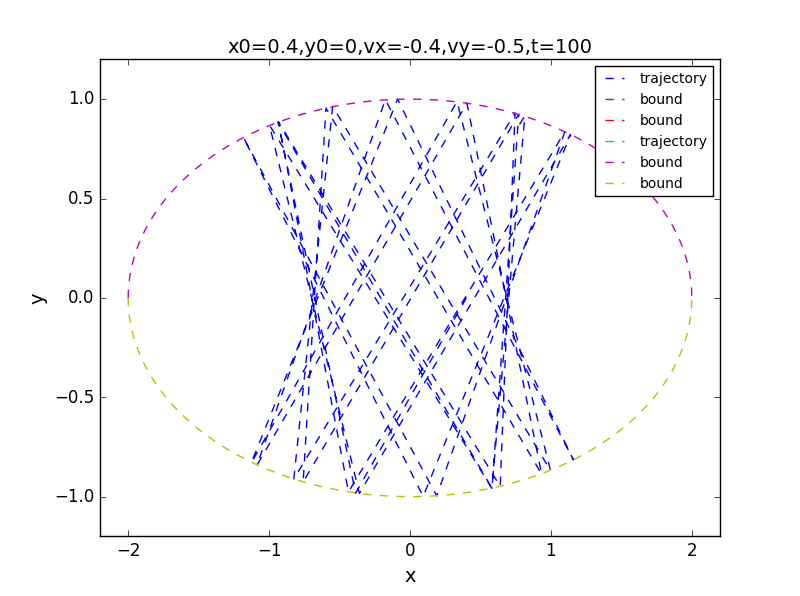
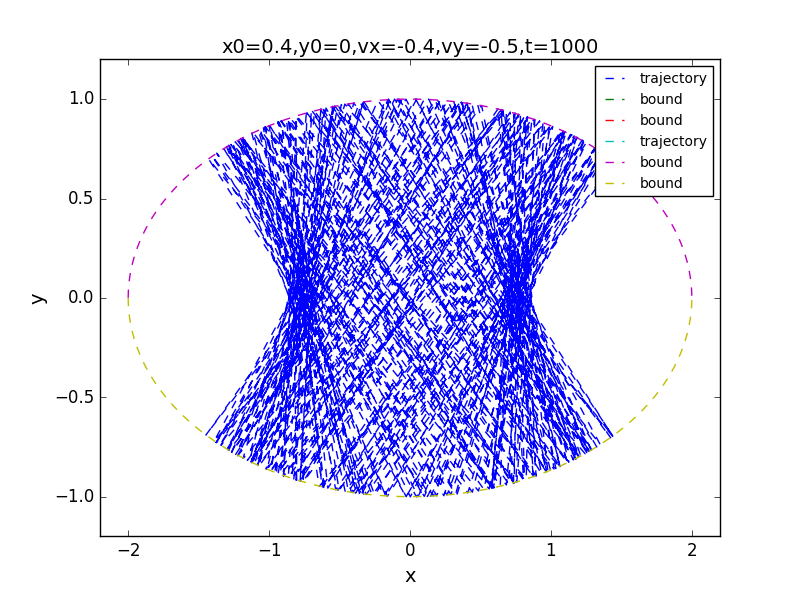
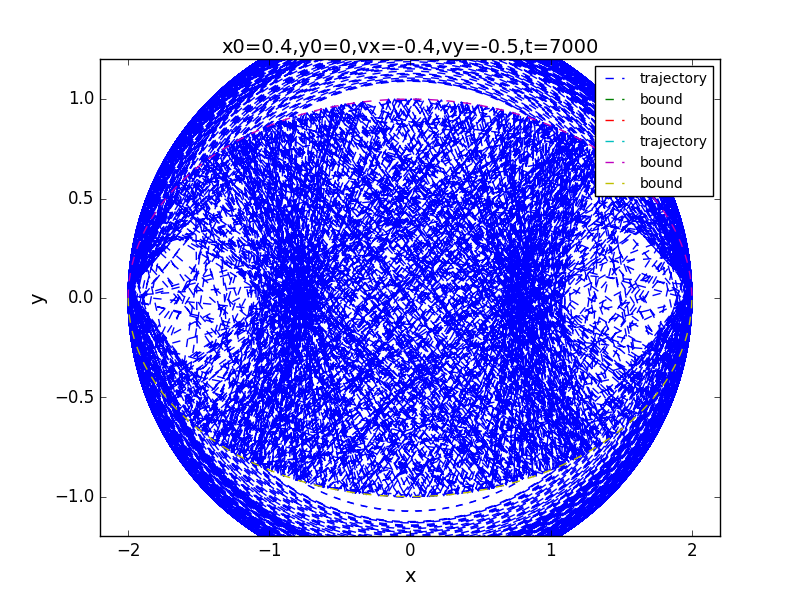
the phase:

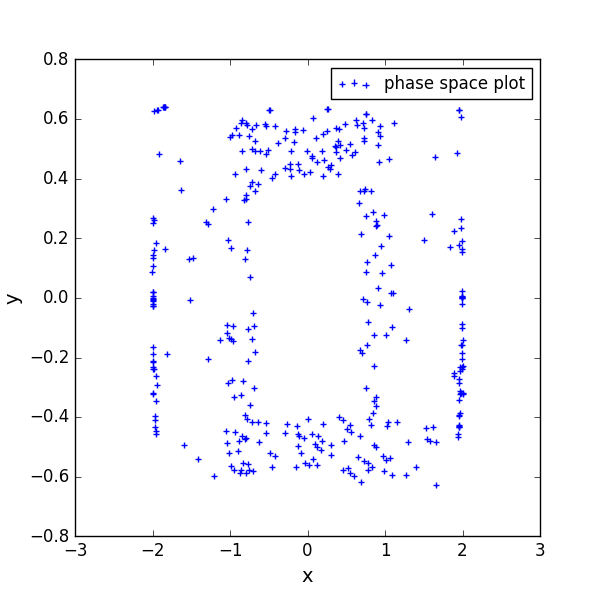
big circle contains small elliptical

for t=100,1000,5000