@74849b 2017-01-04T16:30:45.000000Z 字数 3203 阅读 856

final paper chapter 7:random systems

罗佳佳 2014301510065

background

random walks

We consider a class of systems in which randomness plays a central role.These are called random.Typically,these systems consist of a very large number of "degrees of freedom",which might be associated with particals.

A typical stochastic problem is diffusion;this describes such important processes as the spreading of a drop of cream in coffee.If you place a drop od the cream at the center,eventually,the coffee will take on a uniform brownish color.At a microscopic level,a partical would move for a short period in a straight line,between collision with other cream particles and with coffee particles. Each collision would cause an abrupt change in particle's velocity.

We argue that the motion of a partical or molecule in solution is analogous to a random processes.A routine that implements a random walks in one dimension is illustrated below.We generate a random number in the range between 0 and 1 and compare its value to 1/2,If it is less than 1/2,our walker moves right,otherwise it steps to the lef.This process is then repeated to generate $x_n$ as a function of $n$ .

results:
For constant length: $x$ versus step number for two or three random walks in one dimension:For random lengths in the range -1 to 1:From this example,we find the process is hard to predict.

diffusion

Random walks are equivalent to diffusion.By adopting the cream-in-coffee analogy,we can calculate how these particles are spatially distributed as a function of time.A way to describe the same physics involves the density of particles, $\rho(x,y,z,t)$ .The density is proportional to the probability per unit volume per unit time,denoted by $P(x,y,z,t)$ ,to find a particle at $(x,y,z)$ at time $t$ . $P(i,j,k,n)$ is the probability to find the particle at the site $(i,j,k)$ at time $n$ .Since we are on a simple cubic lattice,there are 6 different nearest sites.The total probability to arrive at $(i,j,k)$ is
$P(i,j,k,n)=\frac 16[P(i+1,j,k,n-1)+P(i-1,j,k,n-1)+$
$P(i,j+1,k,n-1)+P(i,j-1,k,n-1)+$
$P(i,j,k+1,n-1)+P(i,j,k-1,n-1)]$ It can be written as
$\frac{\partial{\rho}}{\partial{t}}={D\nabla^2{\rho}}$ We consider one spatial dimension, $x$ :
$\frac{\partial{\rho}}{\partial{t}}=D\frac{\partial^2{\rho}}{\partial{x}^2}$ We can write $\rho(x,t)=\rho(i\Delta{x},n\Delta{t})=\rho(i,n)$ ,so:
$\rho(i,n+1)=\rho(i,n)+\frac{D\Delta{t}}{(\Delta{x})^2}[\rho(i+1,n)+\rho(i-1,n)$
$-2\rho(i,n)]$

results:
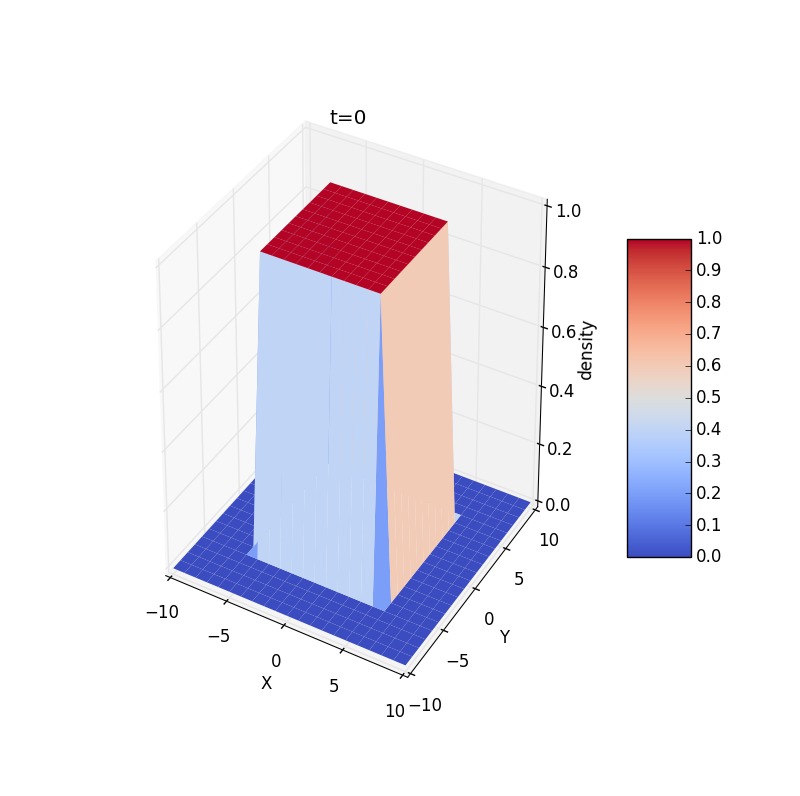
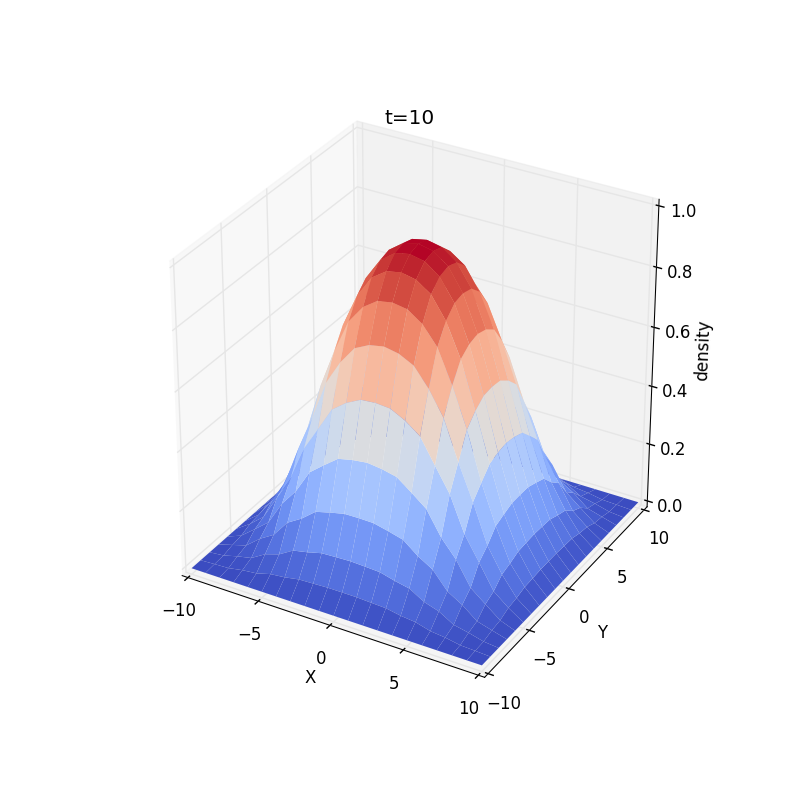
1.schematic solusions of the diffusion equation at four different times.We find the spatial distribution has a Gaussian form whose half-width $\sigma$ is the spatial size occupied by the clump of particles at any time.It roughly satisfies the following realtion: $\rho(x,t)=\frac{1}{\sigma}exp[-\frac{x^2}{2\sigma^2}]$ .As time passes,the width increases as $\sigma\sim\sqrt t$ .
2.A numerical solution of the diddusion equation is shown in the next step:
The density alternates between zero and nonzero values.One way to overcome this problem is to average the results over adjacent grid elements.Doing this yields the results in the following figure:
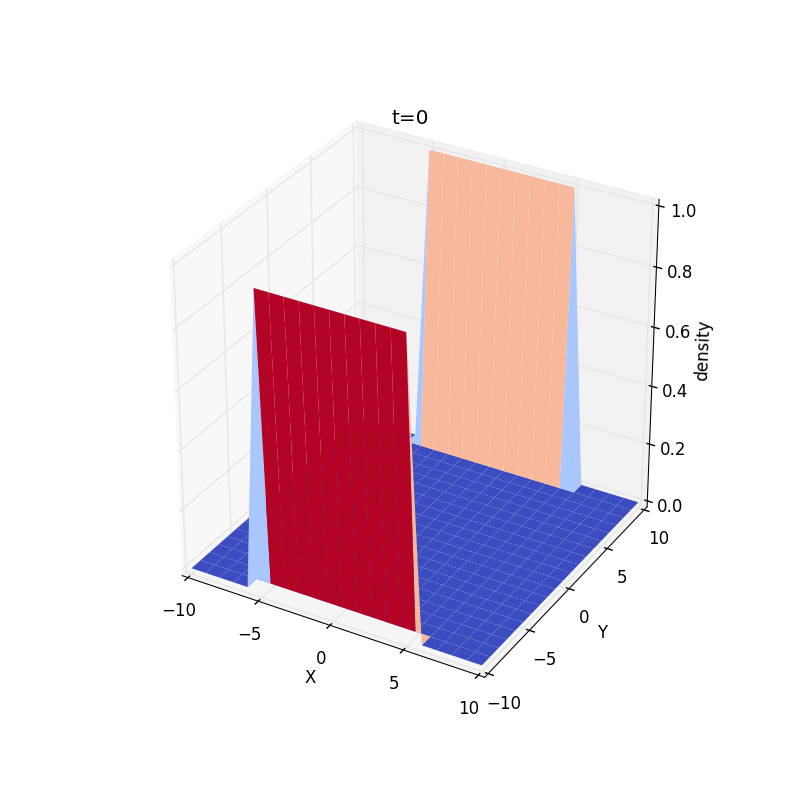
3.We show some results for a two-dimensional case,the all particles are confined to a square region surrounding or away from origin:Change initial conditions:
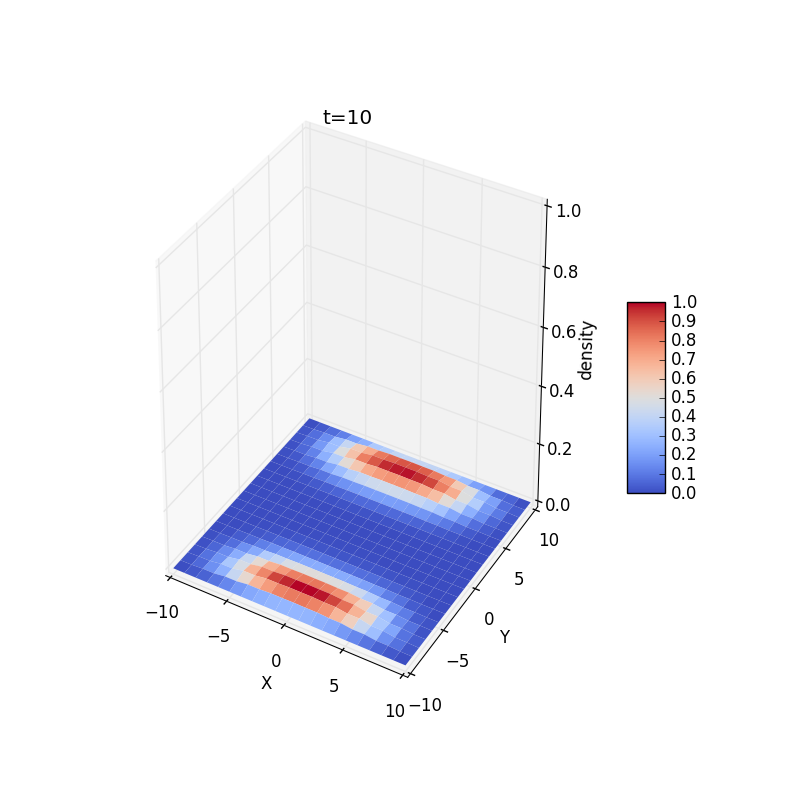
4.For three dimension case,we plot the density at $z=0$ plane.We find it has the same results as two dimension's.
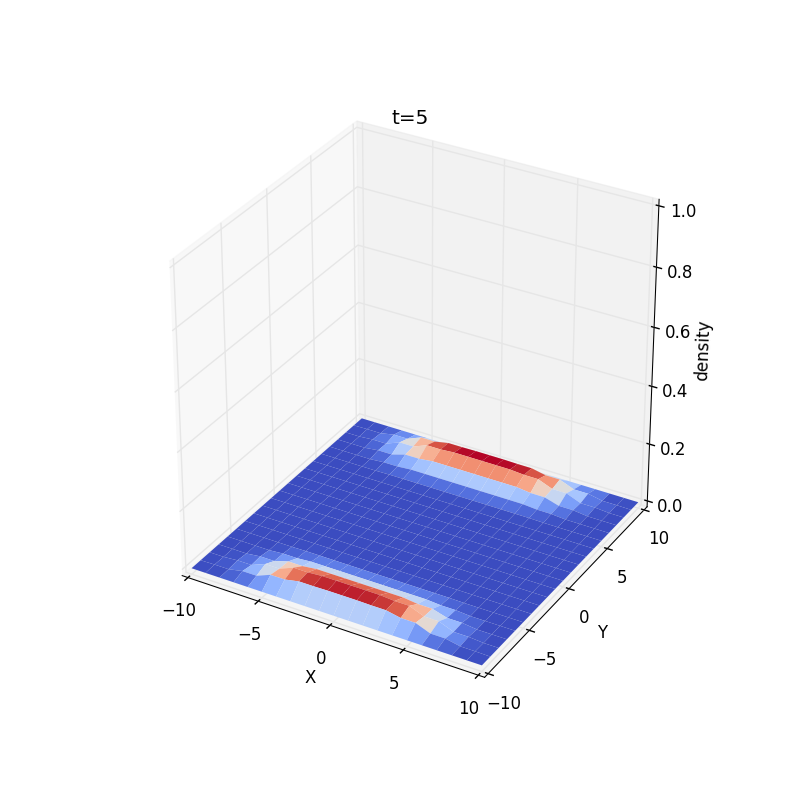
5.Random-walk simulation of diffusion of cream in coffee.
At each time we choose a particle at random and let it take one step in its random walk.These particles are placed in the corner of the region in the initial condition:This results are equivalent to the solution of the two dimensional diffusion equation in the previous discussion.