@EtoDemerzel
2018-01-21T09:07:01.000000Z
字数 2990
阅读 2750
离散数学补充 群论(三)
离散数学 群论
Homomorphism 同态
- Definition: Let and be two groupoids, be a function from to . If for all and in , , then:
- is called a homomorphism from to
- is homomorphic to , denoted by .
is the homomorphic image(同态像) of .
简单来说,就是映射之后的元素依然满足二元关系的对应。
- Definition: Let be a homomorphism from to
- If is an onto(满射,即陪域中任意元素 必有 存在) from to , that is , is called an onto homomorphism from to .
- If is a bijection(双射,又叫一一对应,one-to-one correspondence) from to ,
- is called a isomorphism(同构) from to
- is isomorphic to , or and are isomorphic, denoted by
- Example:

如上图, 的作用是奇偶校验, 二元操作 将两个01串连接在一起。容易看出 是一个同态。
Tips: 要证明是否同态:
- STEP 1. 找到对应关系
- STEP 2. 证明
若要证明是否同构,还需判断 是否为双射.(先判断是否单射,再判断是否满射)- 对于满射同态,单位元和逆元也是对应的。如果 是 广群/半群/独异点/群(或在其基础上加上交换的性质,即Abelian), 与之相同。
- Remember: 同构会保留群的所有性质,只要有性质不同,那么便不是同构。
Fundamental Homomorphism Theorem
- Theorem(Natural Homomorphism 自然同态):
- Let be a congruence relation(即,则有) on a groupoid )
- be the corresponding quotient groupoid(即满足)
Then:
the function defined by
( 对应其等价类)
is an onto homomorphism, called the natural homomorphism.- 证明非常容易。
对任意的, 在 中必存在,则,故 为满射。
, 故为同态。- Theorem(Fundamental Homomorphism Theorem):
- 是广群 到另一个广群 上的一个同态,且是满射。
- 是 上满足如下定理的关系:
, iff
那么,- 是同余关系.
- 和 商广群 (商广群: ) 同构.
- 证明如下:
1.证明 为同余关系: 首先 显然是等价关系。若 , 则。而 是同态,故满足, 则, 为同余关系.
2.证明 和 是同构的:定义,
容易判断 是函数,并且满足单射,(单射是指不同的变量对应不同的值。如果有, 根据定义,, 则 ,我们已经证明 是等价关系,因此 )也满足满射,(由于 是 中的满射函数,容易知道 也是满射函数)。故 是双射。
又因为 .
综上所述,二者同构。- 此定理可以用下图表示:
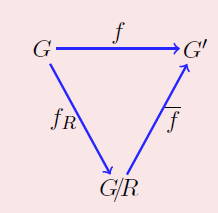
是自然同态,,因为
Normal subgroup
- Definition: 是 群 的子群,, 中, 的由 决定的左右陪集(The left and right coset of in ) 分别是如下集合:
如果 对 都成立,那么子群 是正规子群(Normal subgroup)。
Note: ,并不意味着对于 以及 就有 , 而应该是存在一个 , 使得 。
- Theorem 1:如果 是 群 的一个有限子群, 那么 在 中的每个左陪集的元素个数都和 相同。
Theorem 2(拉格朗日定理):设 是 有限群 的子群,则 的阶(order,即元素个数) 整除G的阶。
同余关系和正规子群:
等价类和陪集:
以下定理说明,群 上的同余关系中 的等价类是正规子群:- Theorem 3: 是群 上的同余关系, (即 这个等价类中包含单位元), 那么 是 的一个正规子群, 并且对于 。
Notice: 商群 是由 的所有左陪集构成的。商群上的操作 定义为:
定义为: 。 是从 到 上的一个同态。( 也写作 )
以下的定理说明,任何一个正规子群,都是某一个同余关系上 的等价类:- Theorem 4: 是群 的一个正规子群, 关系: iff 。 那么 是群 上的同余关系, 是 中的等价类 。
- Corollary: 是从群 到群 的一个同态并且是满射, 的核(kernel), , 定义为 , 那么 是 的一个正规子群, 商群 与 同构。(根据Fundamental homomorphism theorem 2., 可定义同余关系 : , 容易知道 ;根据Theorem 3, 是正规子群, 与 同构。)
