Exercise 13 :$\,$ Problem 6.16

Perform the calculations described in this section.One interesting possibility is to compare the size of the octave stretching,that is,the magnitude of the deviations from a purely harmonic spectrum,for short (treble) and long (bass) strings.The relevant string parameters for a good grand piano are given in Table 6.1

Table 6.1:

Some parameters describing the properties of a strings in a typical grand piano.The note $C4$ is middle $C$ while $C2$ is two octives lower and $C7$ is three octaves higher in frequency.The parameter $b$ is associated with damping,as discussed in problem $6.17$.After chaine and Askenfelt (1994)

$Note$	$f(Hz)$	$L(m)$	$c(m/s)$	$ε(unitless)$	$b(s^{-1})$
$C2$	65.4	1.9	250	$7.5×10^{-6}$	0.5
$C4$	262	0.62	330	$3.8×10^{-5}$	0.5
$C6$	2093	0.09	380	$8.7×10^{-4}$	0.5

Abstract

This article is about using numerical method to solve wave function, especially for a wave spreading in a string. Further more, it will discuss the realistic case, which means considering friction.

Background

In this case, the equation of vertical motion for a point in the string is:

$$ρ△x\frac{d^2y}{dt^2}=Tsinθ_{i+1}-Tsinθ_i \qquad \qquad (1)$$
When $△x$ is sufficient small, we have:
$$△x=dx \qquad sinθ≈tanθ=\frac{∂y}{∂x} \qquad \qquad (2)$$
Then, the equation (1) becomes:
$$\qquad \frac{∂^2y}{∂t^2}=\frac{T}{ρ}\frac{∂^2y}{∂x^2}=c^2\frac{∂^2y}{∂x^2} \qquad \qquad \qquad (3)$$
Also, if we consider the friction, the equation of vertical motion becomes:
$$\qquad \frac{∂^2y}{∂t^2}=c^2(\frac{∂^2y}{∂x^2} -εL^2\frac{∂^4y}{∂x^4})\qquad \qquad$$
In the numerical approach, we rewrite the equation into this form:
$$\frac{y(i,n+1)+y(i,n-1)-2y(i,n)}{(△t)^2}≈c^2[\frac{y(i+1,n)+y(i-1,n)-2y(i,n)}{(△x)^2}] \qquad (5)$$
Rearranging the former expression $y(i,n+1)$ we can express in terms of y at pervious time steps, with the result:
$$\qquad y(i,n+1)=2[1-r^2]y(i,n)-y(i,n-1)+r^2[y(i+1,n)+y(i-1,n)] \qquad (6)$$
where $r=c\frac{△t}{△x}$. Generally, we let $r=1$ to keep the stability for the solution.
Also, in the case of realistic string, the numerical equation becomes:
$$y(i,n+1)=[2-2r^2-6εr^2M^2]y(i,n)-y(i,n-1)$$ $$\qquad\qquad \qquad+r^2[1+4εM^2]\cdot [y(i+1,n)-y(i-1,n)]$$ $$\qquad \qquad \qquad\qquad \qquad \qquad-εr^2M^2[y(i+2,n)+y(i-2,n)] \qquad \qquad \qquad \qquad (7)$$
where $M=\frac{L}{△x}$ is the number of spatial units along the string.

Main body

code1
wxp_1=0, wxp_2=1, and Amp=1: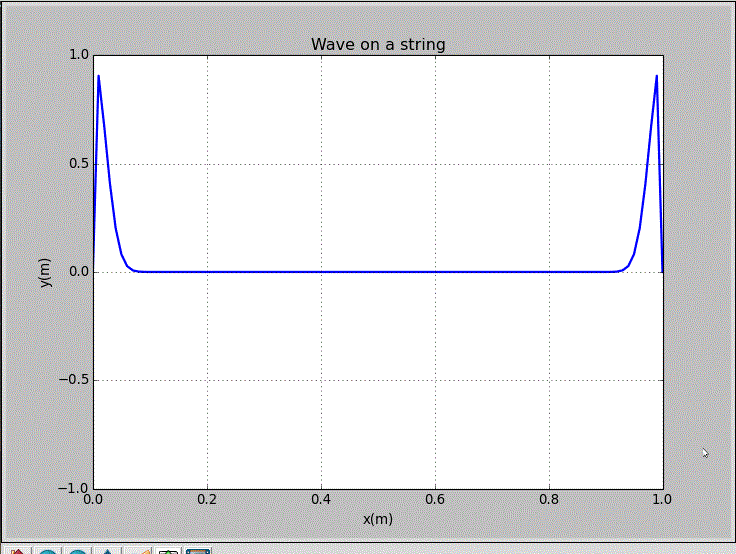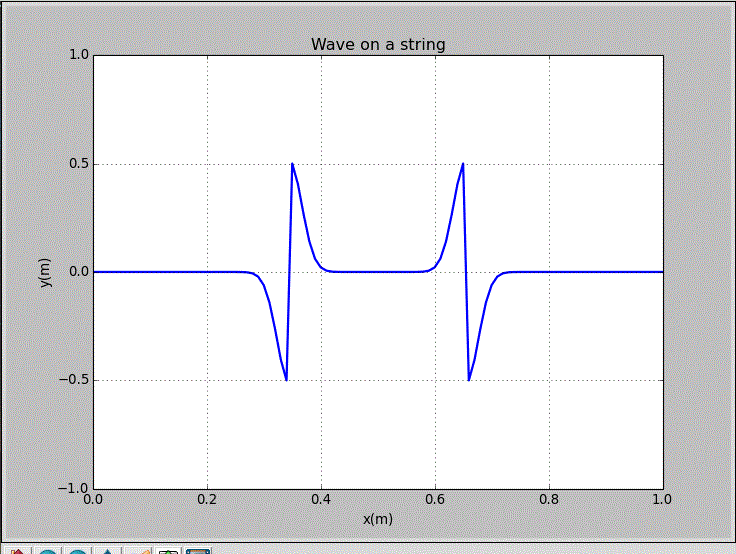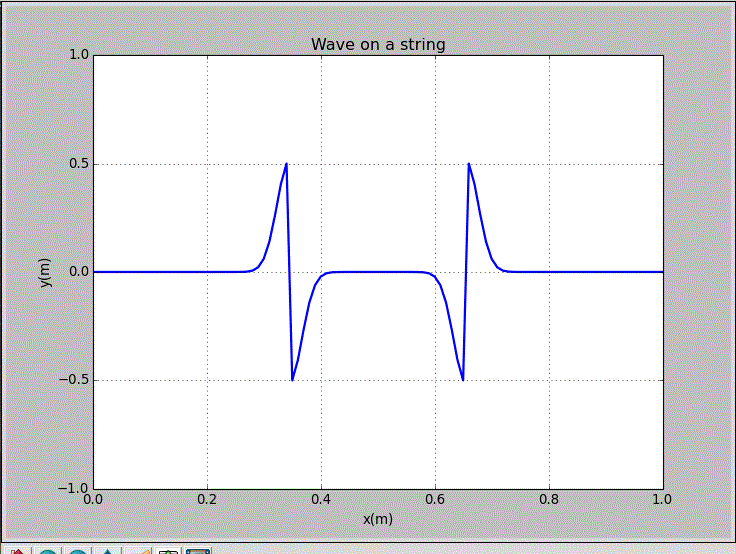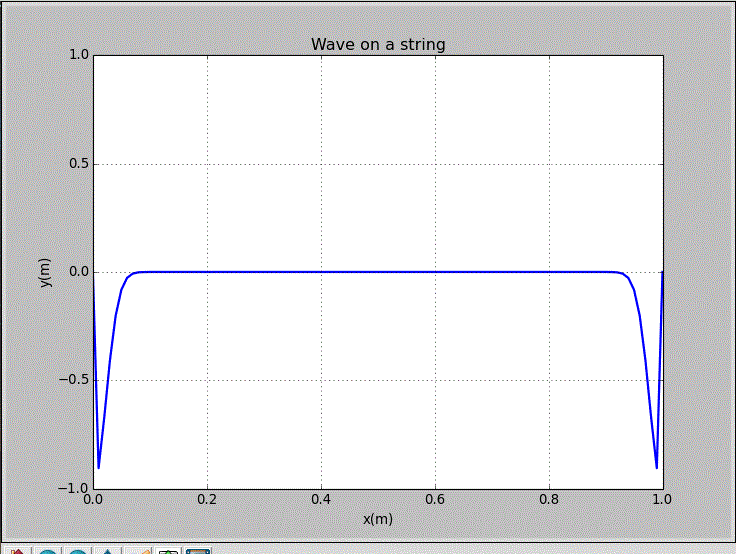

wxp_1=0.1, wxp_2=0.9, and Amp=0.5: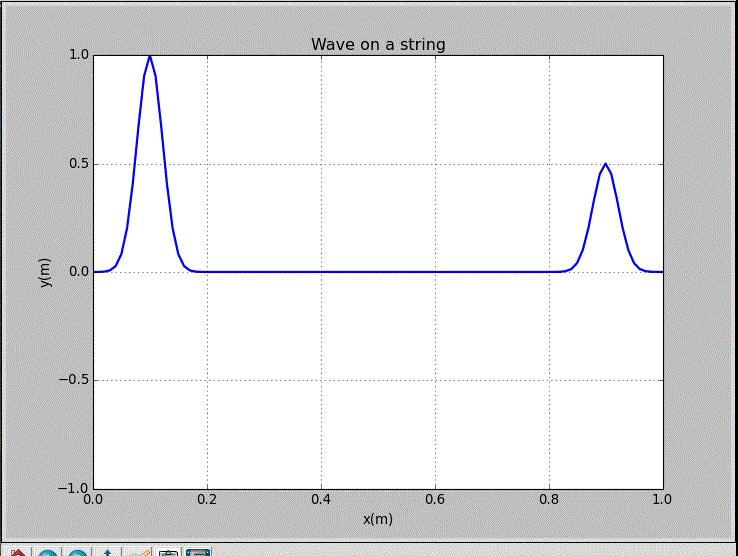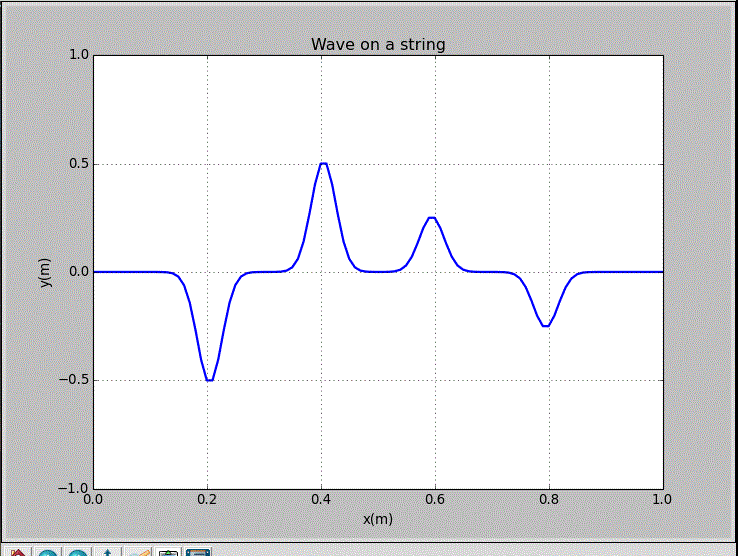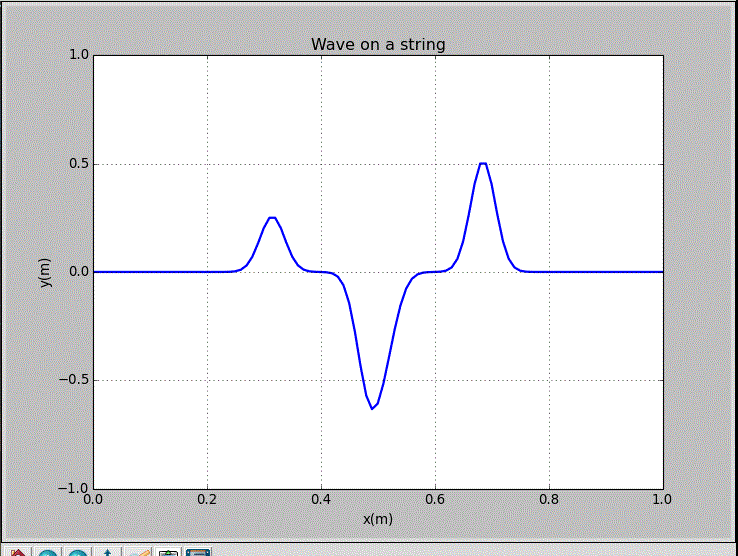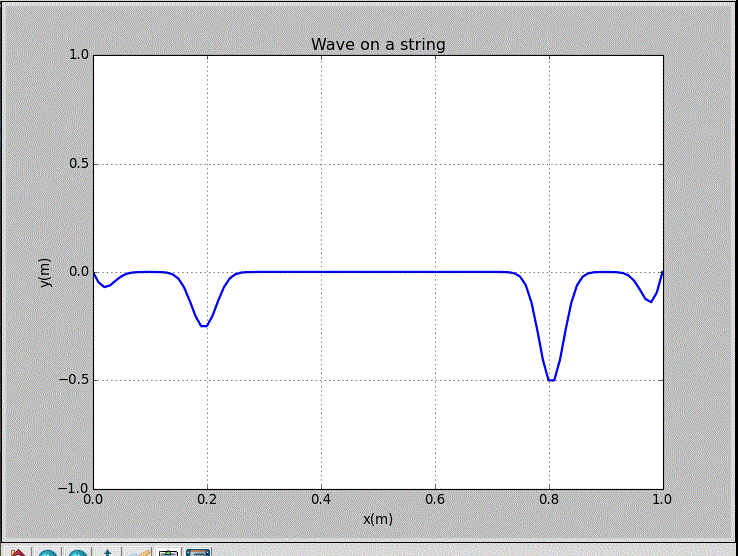

wxp_1=0.2, wxp_2=0.7, and Amp=1.2: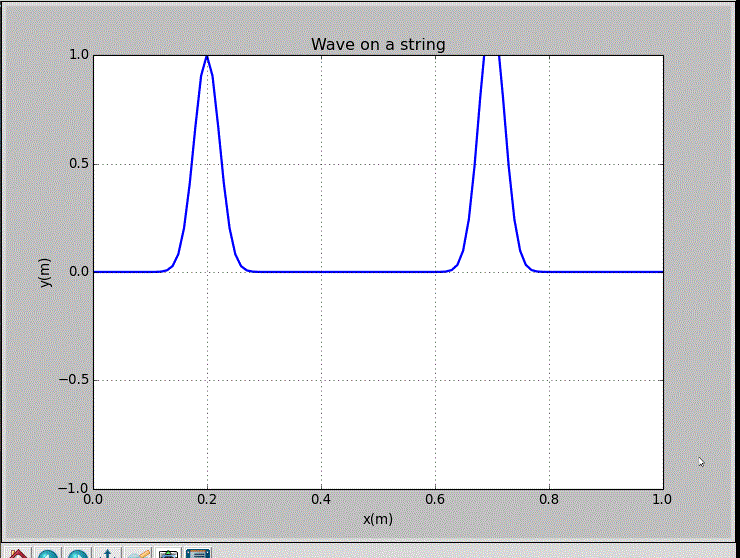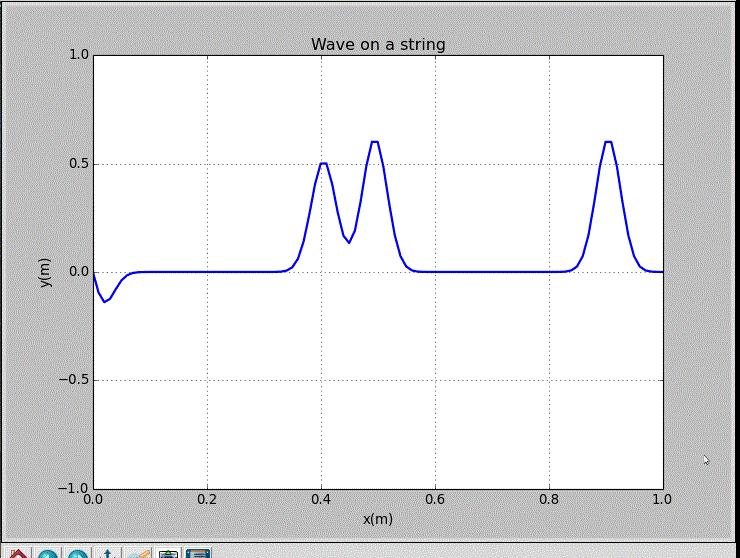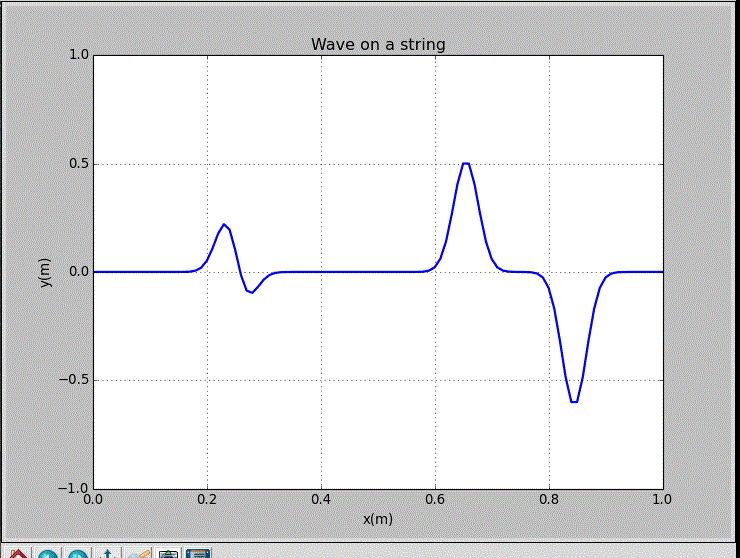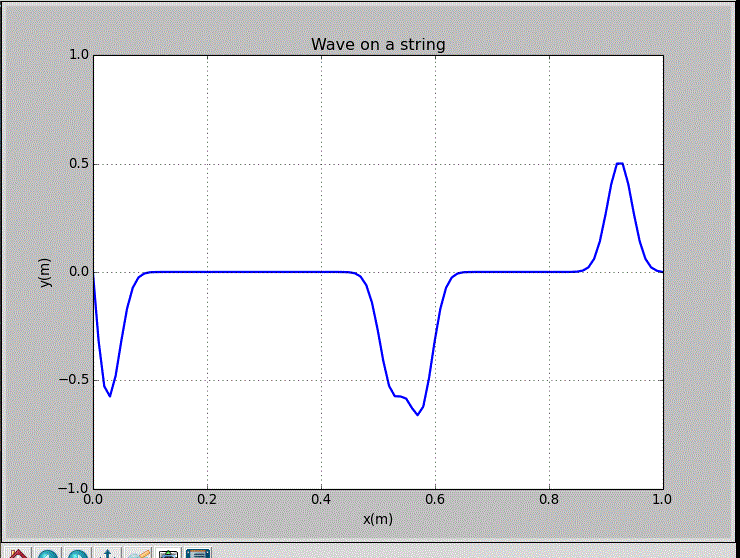

String signal and power spectra for ideal strings

The recording point is x=0.2m.
In this standing wave case, every point on the string does harmonic motion, which means the string signal must be a sine or cosine wave.

This string was excited with a Guassian initial pluck centered at x=0.3m. Either the odd frequencies or the even frequencies were excited in this situation.


This string was excited with a realistic initial pluck centered at x=0.125m. Only a few low frequencies could be excited in this case.

Power spectra for "realistic" strings code2

In this section, I will consider the influence of the friction of the string. In all cases data of the point at x=0.3m was analyzed, and I used $△t=△x/4c$ to ensure stability for all values of employed.
The power spectra for "realistic" string in the case of Guassian pluck.

The power spectra for "realistic" string in the case of realistic pluck.
As the figure showed above, there are large frequency shifts in the high frequency. I construct a high frequency standing wave in order to verify it.

This is what we expect.

Conclusion

The friction of the string will cause a frequency shift especially for the high frequency. Also, the frequencies which excited in a guitar are always low frequencies.

Acknowledgement

1)Giodano, N.J., Nakanishi, H. Computational Physics. Tsinghua University Press, December 2007.
2)Chen Feng