Random systems

$\qquad$$\qquad$$\qquad$武汉大学物院材料班 $\qquad$胡胜勇 $\qquad$ 2014301020090

摘要

由于随机系统不能由初始条件确定或预测，本次作业中我们主要考察随机游走模型中距离平方随时间的变化。在自我避免的步行中，我们还调查平方距离的标准偏差随时间变化。之后，我们建立了偏微分方程扩散模型，并将其与先前的随机游走模型进行比较。最后，考虑熵随时间的变化随机散步方法在奶油的咖啡问题。为了对随机系统有一个粗略的理解，我们探索各种随机游走模型，并研究它们的一些属性,探究了以下几个问题：
1、每次随机行走等单位长度1的粒子的随机行走演示，并计算一维情况下粒子与原点距离的方均根随时间的变化情况
2、每次行走随机单位长度（-1,1）粒子的演示和方均根情况
3、自回避随机行走（self-avoiding walks）
4、分别用“随机行走”的方法和“公式演化”的方法模拟扩散现象，并且拓展到二维情况
5、画散点图模拟“奶油融化在咖啡里”的粒子运动情况

背景

随机行走（random walk）是指基于过去的表现，无法预测将来的发展步骤和方向。核心概念是指任何无规则行走者所带的守恒量都各自对应着一个扩散运输定律 ，对于我们解决热力学问题有很好的辅助作用，，它接近于布朗运动，是布朗运动理想的数学状态
1.

1906年Perrson提出，随机游走是一种基于运用[0,1]区间的均匀分布随机数序列来进行的计算。

2.

1827年植物学家Brown观察到水中的花粉等颗粒可以不停的作无规则运动。我们观察到的Brown 颗粒的运动是大量碰撞的涨落的结果，它是一种完全无规则的随机运动。

3.

醉汉行走问题
Person 在1905 年发表于《Nature》的论文中提出的：
“一个人从θ点出发，沿直线走了l 码，然后他转了一个角度后由沿第二条直线走了l 码，他重复了n 次这样的过程。我想求出n次过程后此人位于离开起始点r到r+dr 距离内的概率”
4.

5

扩散的物理
扩散是由于粒子浓度梯度的存在▽ρ形成粒子往低浓度区域迁移的趋势，单位时间内通过某一方向垂直截面的粒子数即为粒子流密度：$\overrightarrow{j}=-D▽ρ$

6.

马尔可夫(Markov)过程
它在游走中任一阶段的行为都不被先前游走的历史所限制，即区域内的点可以被多次访问，这种随机游走过程叫作马尔可夫(Markov)过程。又因为游走最终会终止在边界上，故而该类随机游走又被称为马尔可夫链。马尔可夫链正是这样生成相继各个状态的，使得后一个状态是由前一个状态和确定的分布所决定。由此可知相继的各状态之间的确存在着关联。所以，马尔可夫链是分子动力学中有运动方程生成的轨道在概率方面的对应物。

7.

自规避随机游走(self-avoiding walks)
在随机游走的过程中，任何一个的游走概率都要考虑前面游走的历史，因而游走有可能碰到边界前就被强行终止掉。

正文

1.1一维方向上单位长度的随机行走（$a_1和a_2各运行一万步$）

1一维方向上单位长度的随机行走代码

运行结果1

运行结果2

运行结果3

由于是随机行走，每运行一次，结果将完全不同

1.2随时间的变化关系

随时间的变化关系代码

运行结果1

用计算机拟合的线性方程是0.95110425 x + 0.82500290

运行结果2

用计算机拟合的线性方程是1.01119660 x - 0.14134479

2.1一维方向上（-1,1）随机距离的随机行走

运行结果1

运行结果2

运行结果3

由于是随机行走，每运行一次，结果依然会完全不同

运行结果1

程序的拟合直线为0.3269077 x +0.18974918，斜率约为一维方向上单位长度的随机行走的$\frac{1}{3}$

运行结果2

程序的拟合直线为0.33996418 x - 0.37724803， 斜率约为一维方向上单位长度的随机行走的$\frac{1}{3}$

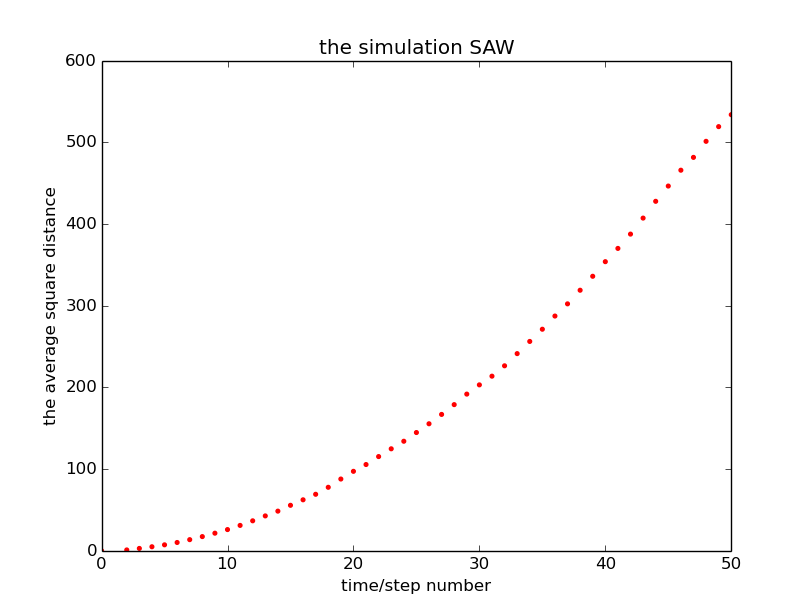
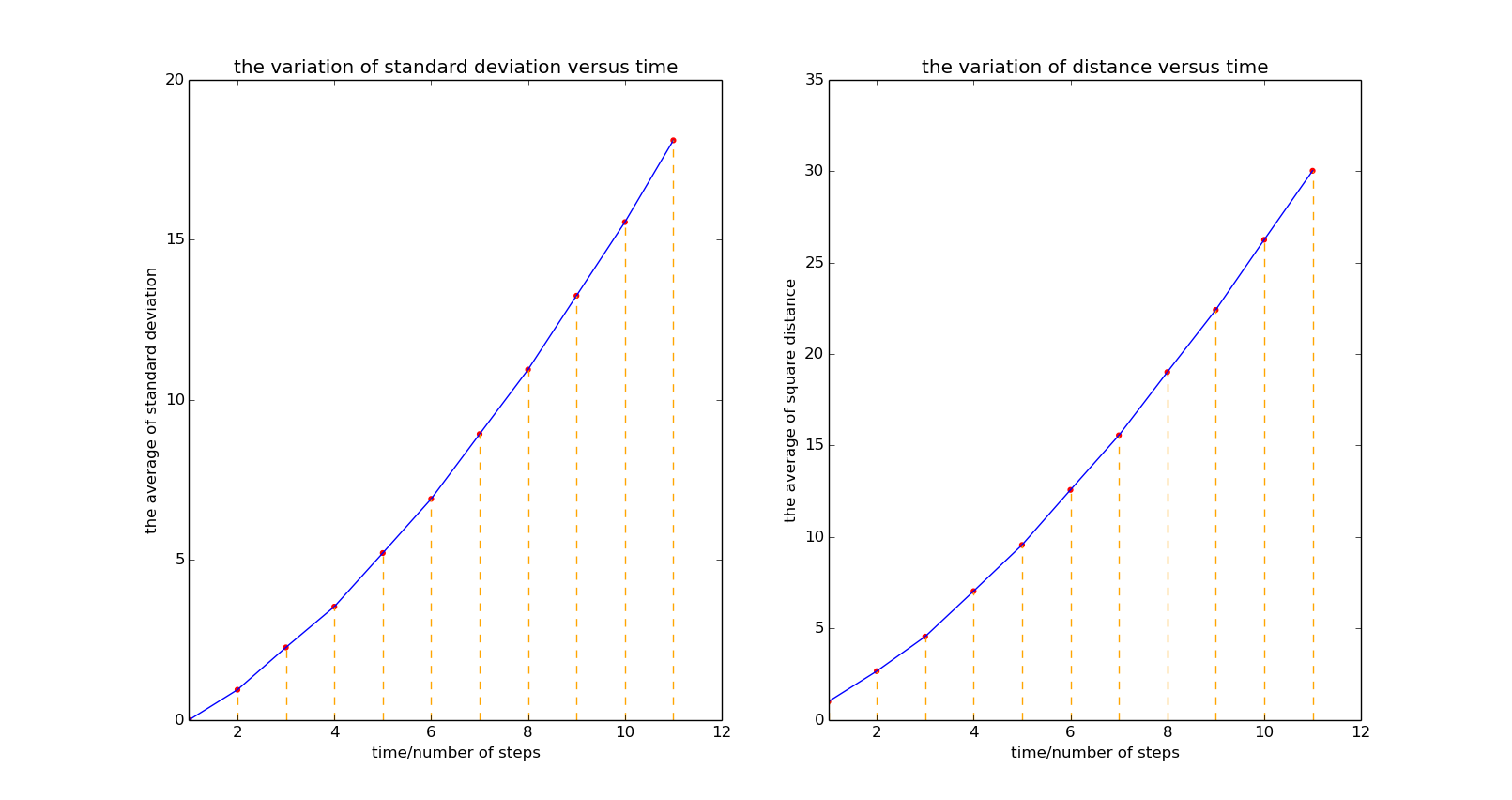
3.自回避随机行走（self-avoiding walks）

$\qquad$为了研究大分子的形状，它是线形的，但不能相交，这意味着在一个位置只能被占据一次。 我们只研究二维SAW。 在这种情况下，我们设计SAW模型，即随机游走粒子的路径将不会通过它之前已经通过的位置。 为了完成这个目标，我们必须扫描前面步骤的位置，以查看它是否占据了与当前粒子位置相邻的四个位置。 如果一些已经被占用，粒子现在不能通过它们。
$\qquad$另一个生动的例子是假想把一条狗放置在一个大城市的中心位置，大城市的街道构成我们所熟悉的网格模式。假设城市包括n条南北走向的街道和n条东西走向的街道，所有的街道均匀分布交叉构成一个网格。这条狗试图逃出城市，在每个交叉路口随机选择方向，但通过狗的灵敏嗅觉不走重复的路。但有时候这条狗会走入死胡同，即在某些交叉路口没有选择，必须重走已经走过的交叉路口。(来自网络)
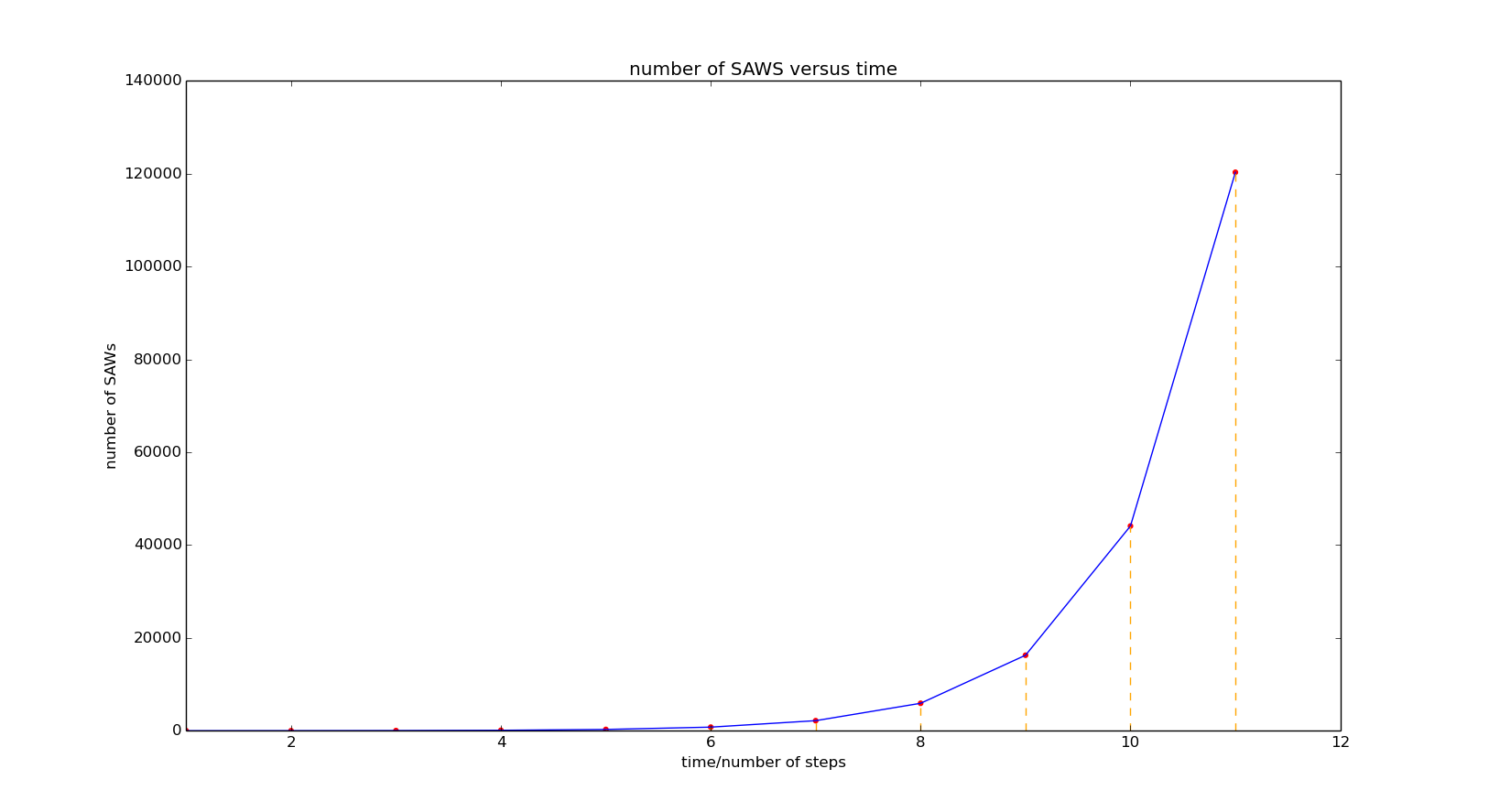
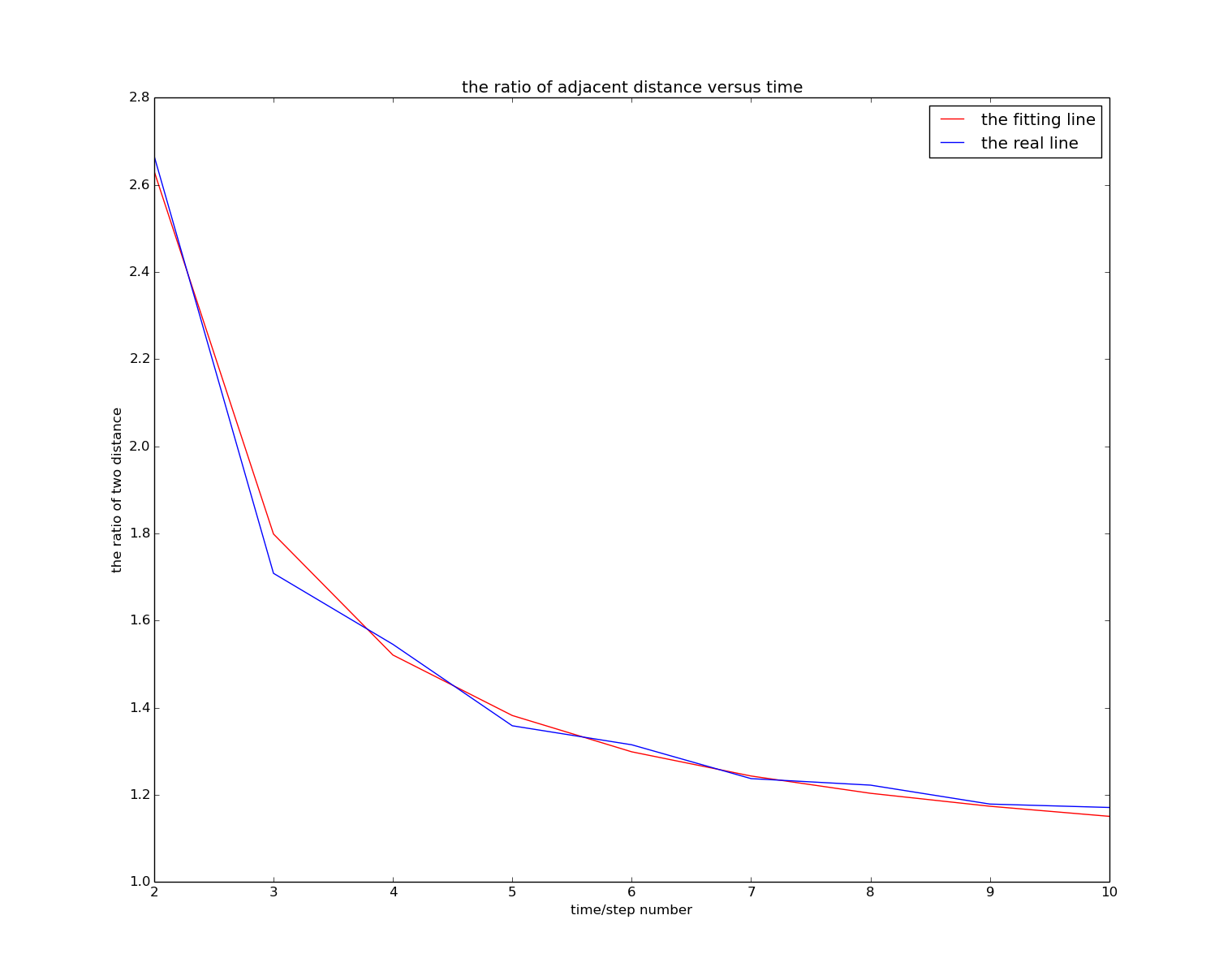
$\qquad$有两种方法来实现这一目标：一种是模拟，另一种是枚举。 模拟是首先产生许多随机游走路径，如果它已经自相交，然后放弃它们，所以其余的可以是所有SAW路径。 枚举是逐步列出可能的SAW路径的方法。

$$\sqrt{r^2}~At^v$$

$$\qquad$$

$$\qquad$$

$$\qquad$$

$$\qquad$$

$$\qquad$$

附：

4.用“随机行走”的方法和“公式演化”的方法模拟扩散现象，并且拓展到二维情况

一维扩散（随机行走法解决） 一维扩散（随机行走法解决）代码

一维扩散（计算推演解决）一维扩散（计算推演解决）代码

二维扩散（计算推演解决）二维扩散（计算推演解决）代码

相比于随机行走法，计算法还是较好，得出来的图像较为平滑

5.画散点图模拟“奶油融化在咖啡里”的粒子运动情况 代码

熵增 代码

结论

1.对于一维的单位长度随机行走，粒子在原点附近摆动，随时间线性增加。随机距离（-1~1）时，结论不变，随时间线性增加速度降低。

2.通过探索几种随机游走模型，我们可以说，它对于许多随机系统在一定程度上是一个很好的近似。 它以某种方式揭示了这种系统的本质。 然而，为了得出实际情况，我们不能省略粒子之间的相互作用。 一旦我们将这个因素添加到模拟中，毫无疑问，结果将吸引现实，但就像SAW，计算将随着时间步长的增加而变得非常大。

3.“随机行走”的方法和“公式演化”的方法都可以模拟扩散现象，但公式法显然精准一些，但随着样本数量上升，随机模拟的方法也会越来越准确，并且，后者思想简单，在较高运算条件下能解决的问题更多

参考

Computational Physics, Nicholas J. Giordano & Hisao Nakanishi
《Python基础教程》
百度百科
计算物理RandomSystems Xiaobao Yang ，Department of Physics，华南理工大学
计算物理-随机游走