第四次作业

---

作业1.5

---

摘要

本次作业研究的是两种放射性原子核A和B之间进行的衰变，原子核A会衰变成原子核B，而原子核B也会衰变成原子核A。题目要求我们研究A和B原子核的数量随时间的变换。并改变不同的初始条件后证实当系统稳定时，A和B原子核的数量是常量。

---

背景

题目原文：
1.5. Consider again a decay problem with two types of nuclei A and B, but now suppose that nuclei of type A decay into type B, while nuclei of type B decay into type A. Strictly speaking, this is not a "decay" process, since it is possible for the type B nuclei to turn back into type A. A better analogy would be a resonance in which a system can tunnel or move back and forth between two states A and B which have equal energies. The corresponding rate equations are

$$\frac{dN_A}{{\rm d}t}=\frac{N_B}{τ}-\frac{N_A}{τ}，$$
$$\frac{dN_B}{{\rm d}t}=\frac{N_A}{τ}-\frac{N_B}{τ}，$$
where for simplicity we have assumed that the two types of decay are characterized by the same time constant . Solve the system of equations for the numbers of nuclei, and , as functions of time. Consider different initial confitions, such as =100, =0, etc., and take =1 s. Show that your numerical results are consistent with the idea that the system reaches a steady state in which and are constant. In such a steady state, the time derivatives and should vanish.

---

正文

编程思路与课堂上所讲大同小异，由题目所给条件及泰勒展开可得：

$$N_A(t+Δ)≈N_A(t)+\frac{N_B}{τ}-\frac{N_A}{τ}，$$
$$N_B(t+Δ)≈N_B(t)+\frac{N_A}{τ}-\frac{N_B}{τ}，$$
按课上所讲思路，代码如下：

import pylab as pl
class uranium_decay:
    def __init__(self, number_of_nuclei_A = 100, number_of_nuclei_B = 0 , time_constant = 1, time_of_duration = 5, time_step = 0.05):
        self.n_uranium_A = [number_of_nuclei_A]
        self.n_uranium_B = [number_of_nuclei_B]
        self.t = [0]
        self.tau = time_constant
        self.dt = time_step
        self.time = time_of_duration
        self.nsteps = int(time_of_duration // time_step + 1)
        print("Initial number of nuclei A ->", number_of_nuclei_A)
        print("Initial number of nuclei B ->", number_of_nuclei_B) 
        print("Time constant ->", time_constant)
        print("time step -> ", time_step)
        print("total time -> ", time_of_duration)
    def calculate(self):
        for i in range(self.nsteps):
            tmp_A = self.n_uranium_A[i] - self.n_uranium_A[i] / self.tau * self.dt+self.n_uranium_B[i] / self.tau * self.dt
            tmp_B = self.n_uranium_B[i] - self.n_uranium_B[i] / self.tau * self.dt+self.n_uranium_A[i] / self.tau * self.dt
            self.n_uranium_A.append(tmp_A)
            self.n_uranium_B.append(tmp_B)
            self.t.append(self.t[i] + self.dt)
    def show_results(self):
        pl.plot(self.t, self.n_uranium_A)
        pl.plot(self.t, self.n_uranium_B)
        pl.xlabel('time ($s$)')
        pl.ylabel('Number of Nuclei A and B')
        pl.show()
    def store_results(self):
        myfile = open('nuclei_decay_data.txt', 'w')
        for i in range(len(self.t)):
            print'self.t[i], self.n_uranium_A[i], self.n_uranium_B[i], file = myfile'
        myfile.close()
a = uranium_decay()
a.calculate()
a.show_results()

---

结论

当t=0时，原子核A的数量为100，原子核B的数量为0，时间常量设置为1。模拟结果如图所示：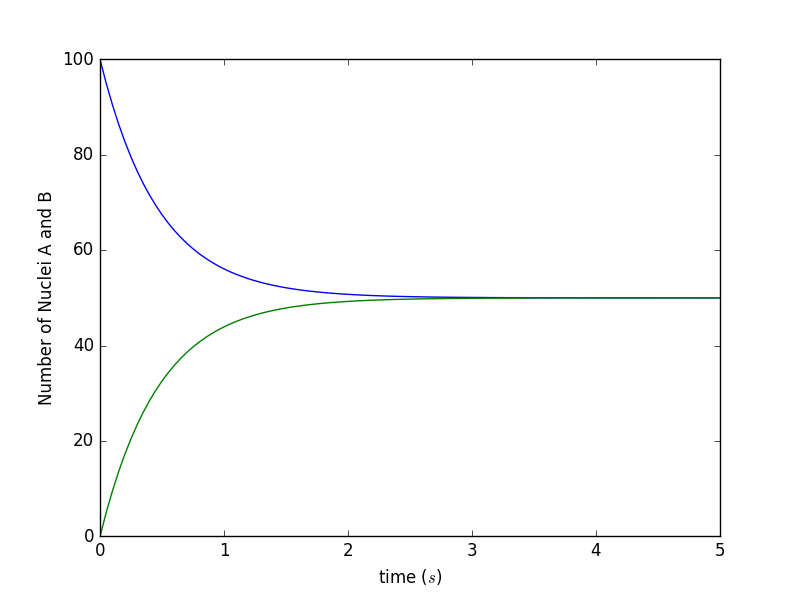

当t=0时，原子核A的数量为100，原子核B的数量为20，时间常量设置为1。模拟结果如图所示：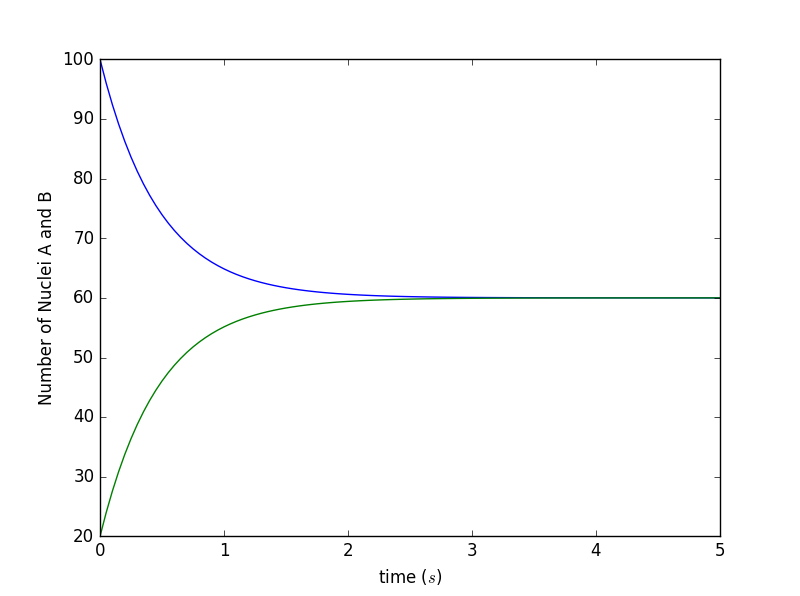

由实验结果所得：原子核A和原子核B的数量会逐渐趋于一致，且两种原子核数量的变化率变为0。

---

致谢

感谢蔡浩老师将课堂ppt及代码传到网上给我们参考。