第八次作业

作业3.20

摘要

画出bifurcation图像，估算Feigenbaum系数。

背景

题目原文：
3.20:Calculate the bifurcation diagram for the pendulum in the vicinity of Fd=1.35 to 1.5. Make a magnified plot of the diagram and obtain an estimate oof the Feigenbaum parameter.

正文

import pylab as pl
import math
class chaotic_pendulums :
    def __init__(self,i=0,initial_theta=0.2,time_step=0.04,total_time=200.0,length=9.8,\
                 g=9.8, initial_omega=0,q=0.5,Fd=1.35,omegaD=2.0/3.0,df=0.001):
        self.theta=[initial_theta]
        self.t=[0]
        self.omega=[initial_omega]
        self.dt=2*math.pi/1000.0*omegaD
        self.time=total_time
        self.g=g 
        self.l=length
        self.q=q
        self.omegaD=omegaD
        self.a=[0]
        self.b=[0]
        self.Fd=[Fd]
        self.dF=df
    def pendulums(self):
        while (self.Fd[-1]<=1.5):
            _time=0
            while(_time<self.time):
                self.omega.append(self.omega[-1]-((self.g/self.l)*math.sin(self.theta[-1])+\
                     self.q*self.omega[-1]-self.Fd[-1]*math.sin(self.omegaD*self.t[-1]))*self.dt)            
                self.theta.append(self.theta[-1]+self.omega[-1]*self.dt)
                self.t.append(_time)            
                _time += self.dt
                if(self.theta[-1]>=math.pi):
                    self.theta[-1]=self.theta[-1]-2*math.pi
                if(self.theta[-1]<=-math.pi):
                    self.theta[-1]=self.theta[-1]+2*math.pi 
                if(self.t[-1]%(2*math.pi/self.omegaD)<0.002 and self.t[-1]/(2*math.pi/self.omegaD)>15.0):
                    self.b.append(self.theta[-1])
                    self.Fd.append(self.Fd[-1])
            self.Fd[-1]+=self.dF
    def show_result(self):
        pl.plot(self.Fd,self.b,'.')
        pl.xlabel('Fd')
        pl.ylabel('angle($radians$)')
        pl.xlim(1.35,1.50)
        pl.ylim(1.0,3.0)
        pl.show()        
a =chaotic_pendulums()
a.pendulums()
a.show_result()

结论

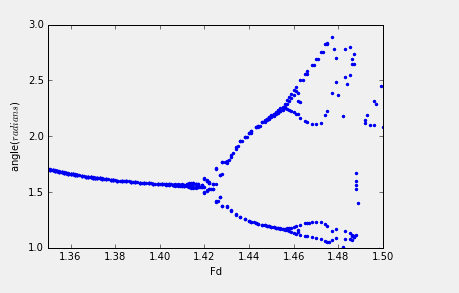
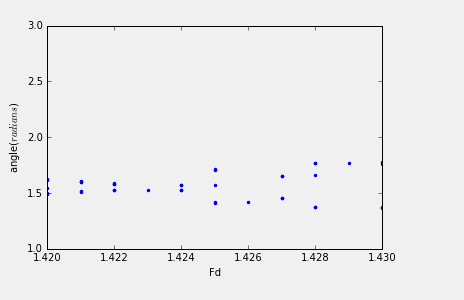
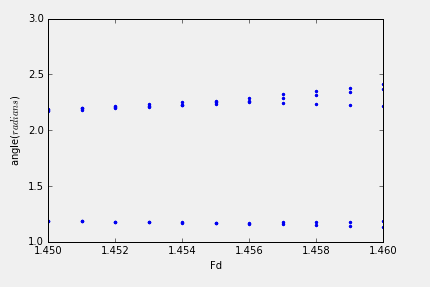
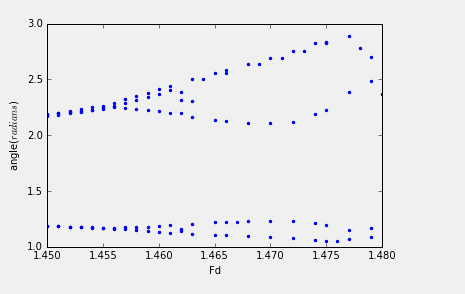
致谢

感谢秦大粤同学和徐秋豪同学。