第九次作业

---

作业3.30

---

摘要

探究Lyapunov指数

---

背景

题目原文：
3.30:Investigate the Lyapunov exponent of the stadium billiard for several values of α. You can do this qualitatively by examining the behavior for only one set of initial conditions for each value of you consider, or more quantitatively by averaging over a range of initial conditions for each value of α.

---

正文

$${dx \over dt}=v_x$$ $${dy \over dt}=v_y$$ $$\vec{v_{i,\bot}}=(\vec{v_i}\cdot\vec{n})\vec{n}$$ $$\vec{v_{i,\mid\mid}}=\vec{v_i}-\vec{v_{i,\bot}}$$ $$\vec{v_{f,\bot}}=-\vec{v_{i,\bot}}$$ $$\vec{v_{f,\mid\mid}}=\vec{v_{i,\mid\mid}}$$

import math
import pylab as pl
import numpy as np
class qwer:
        def __init__(self,vx=1,vy=0,x=0,y=0.1,dt=0.01,dtt=0.00001,tt=100,x0=0.01):
            self.vx=[vx]
            self.vy=[vy]
            self.x=[x]
            self.y=[y]
            self.t=[0]
            self.dt=dt
            self.dtt=dtt
            self.tt=tt
            self.x0=x0
        def run(self):
            while self.t[-1]<self.tt:
                self.vx.append(self.vx[-1])
                self.vy.append(self.vy[-1])
                self.x.append(self.x[-1]+self.vx[-1]*self.dt)
                self.y.append(self.y[-1]+self.vy[-1]*self.dt)
                self.t.append(self.t[-1]+self.dt)
                while self.x[-1]>self.x0 and math.sqrt((self.x[-1]-self.x0)**2+self.y[-1]**2)>1:
                    while math.sqrt((self.x[-1]-self.x0)**2+self.y[-1]**2)>1:
                        self.x[-1]=self.x[-1]-self.vx[-1]*self.dtt
                        self.y[-1]=self.y[-1]-self.vy[-1]*self.dtt
                        self.t[-1]=self.t[-1]-self.dtt
                    else:
                        temp=(self.vx[-1]*(self.x[-1]-self.x0)+self.vy[-1]*self.y[-1])/((self.x[-1]-self.x0)**2+self.y[-1]**2)
                        self.vx[-1]=self.vx[-1]-2*temp*(self.x[-1]-self.x0)
                        self.vy[-1]=self.vy[-1]-2*temp*self.y[-1]
                while self.x[-1]<-self.x0 and math.sqrt((self.x[-1]+self.x0)**2+self.y[-1]**2)>1:
                    while math.sqrt((self.x[-1]+self.x0)**2+self.y[-1]**2)>1:
                        self.x[-1]=self.x[-1]-self.vx[-1]*self.dtt
                        self.y[-1]=self.y[-1]-self.vy[-1]*self.dtt
                        self.t[-1]=self.t[-1]-self.dtt
                    else:
                        temp=(self.vx[-1]*(self.x[-1]+self.x0)+self.vy[-1]*self.y[-1])/((self.x[-1]+self.x0)**2+self.y[-1]**2)
                        self.vx[-1]=self.vx[-1]-2*temp*(self.x[-1]+self.x0)
                        self.vy[-1]=self.vy[-1]-2*temp*self.y[-1]
                while -self.x0<self.x[-1]<self.x0 and (self.y[-1]>1 or self.y[-1]<-1):
                    while self.y[-1]>1 or self.y[-1]<-1:
                        self.x[-1]=self.x[-1]-self.vx[-1]*self.dtt
                        self.y[-1]=self.y[-1]-self.vy[-1]*self.dtt
                        self.t[-1]=self.t[-1]-self.dtt
                    else:
                        self.vy[-1]=-self.vy[-1]
        def show_phase_space(self):
            temp_x=[]
            temp_y=[]
            temp_vx=[]
            for i in range(len(self.y)):
                if math.fabs(self.y[i])<0.001:
                    temp_y.append(self.y[i])
                    temp_x.append(self.x[i])
                    temp_vx.append(self.vx[i])
            pl.plot(temp_x,temp_vx,'.',label="dtt=%f"%self.dtt)
            pl.legend(loc='center right',frameon=True)
            pl.xlabel("x")
            pl.ylabel("$V_x$")
            pl.title("stadium billiard:$\delta$=%.3f"%self.x0)
            pl.xlim(-1,1)
            pl.grid(True)
            pl.show()
        def show_trajectory(self):
            pl.plot(self.x,self.y,label="dtt=%f"%self.dtt)
            pl.legend(loc='upper right',frameon=True)
            pl.title("sadium billiard trajectory $\delta$=%.3f"%self.x0)
            pl.xlabel("x")
            pl.ylabel("y")
            pl.grid(True)
            pl.xlim(-1.5,1.5)
class lyapunov(qwer):
    def cal(self):
        self.divg=[]
        self.lndivg=[]
        self.temp1x=[]
        self.temp1y=[]
        self.temp1t=[]
        self.temp2x=[]
        self.temp2y=[]
        self.temp2t=[]
        self.tempt=[]
        self.initial_seperation=0.00001
        a=qwer(y=0.1)
        a.run()
        self.temp1x=a.x
        self.temp1y=a.y
        self.temp1t=a.t
        a=qwer(y=0.1-self.initial_seperation)
        a.run()
        self.temp2x=a.x
        self.temp2y=a.y
        self.temp2t=a.t
        tmp=min(len(self.temp1x),len(self.temp2x))
        for i in range(tmp):
            self.divg.append(math.sqrt((self.temp1x[i]-self.temp2x[i])**2+(self.temp1y[i]-self.temp2y[i])**2))
            self.lndivg.append(math.log(self.divg[i]))
            self.tempt.append(max(self.temp1t[i],self.temp2t[i]))
    def show_divergence(self):
        pl.plot(self.tempt,self.lndivg,label="initial seperation=%f"%self.initial_seperation)
        pl.title("divergence of two trajectories:$\delta$=%.4f"%self.x0)
        pl.xlabel("time")
        pl.ylabel("ln($\Delta R$)")
        pl.legend(loc="lower right",frameon=True)
        tt=[]
        dd=[]
        for i in range(4000):
            tt.append(self.tempt[i])
            dd.append(self.lndivg[i])
        z=np.polyfit(tt,dd,1)
        p=np.poly1d(z)
        print(p)
        linspx=np.linspace(0,50)
        linspy=z[0]*linspx+z[1]
        pl.plot(linspx,linspy)
b=lyapunov()
b.cal()
b.show_divergence()   

结论

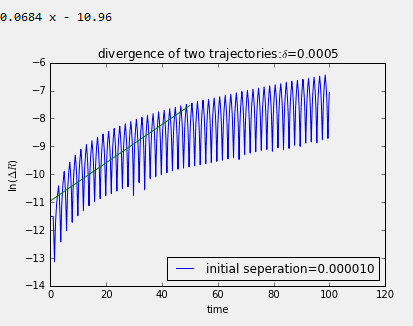
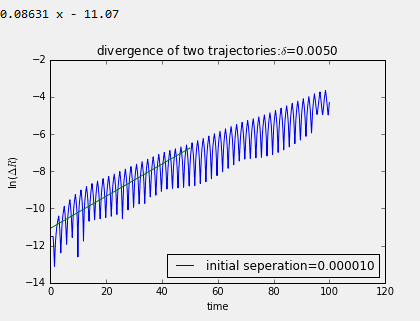
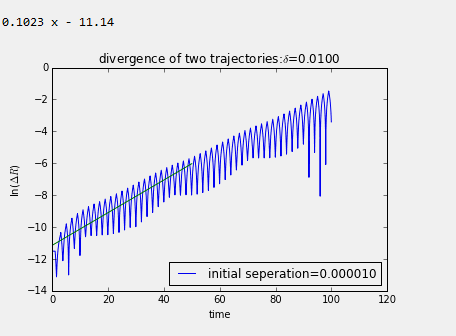
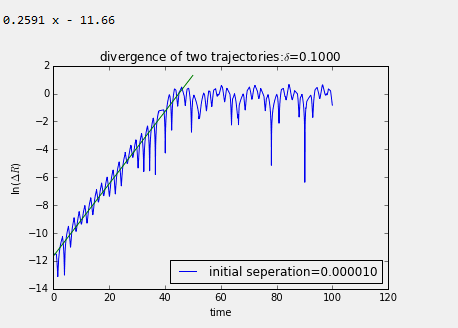
可以看出α不同时，Lyapunov指数截然不同。α越小时，曲线越密集，说明系统经历了更多的状态。

致谢

感谢秦大粤和徐秋豪同学。