第七次作业

---

作业3.13

---

摘要

计算混沌系统中两个单摆的运动差别,并得出Lyapunov指数.

---

背景

题目原文：
3.13:Write a program to calculate and compare the behavior of two,nearly identical pendulums.Use it to calculate the divergence of two nearby trajectories in the chaotic regime,as in Figure 3.7,and and make a qualitative estimate of the corresponding Lyapunov exponent from the slope of a plot of log(Δθ) as a function of t.

---

正文

关系式：

$$\frac{dw}{dt}=-\frac{g}{l}sinθ-q\frac{dθ}{dt}+F_Dsin(Ω_Dt)$$
$$\frac{dθ}{dt}=ω$$
$$ω_{i+1}=ω_i+[-\frac{g}{l}sinθ_i-qω_i+F_Dsin(Ω_Dt_i)]Δ_t$$
$$θ_{i+1}=θ_i+ω_{i+1}Δ_t$$

代码如下：

import pylab as pl
import numpy as np
import math
class chaotic_pendulums:
    def __init__(self,length=9.8,q=0.5,initial_theta=0.2,initial_theta1=(0.2-0.001),initial_omega=0,initial_omega1=0,F_d=1.2,Omega_d=2.0/3,step_time=0.04,total_time=120):
        self.theta=[initial_theta]
        self.omega=[initial_omega]
        self.theta1=[initial_theta1]
        self.omega1=[initial_omega1]
        self.d_theta=[math.log(0.001)]
        self.dt=step_time
        self.l=length
        self.q=q
        self.total_time=total_time
        self.fd=F_d
        self.omegad=Omega_d
        self.t=[0]
        self.n=int(total_time/step_time)
    def pendulum(self):
        while self.t[-1]<=self.total_time:
            temp_omega=self.omega[-1]+(-9.8/self.l*math.sin(self.theta[-1])-self.q*self.omega[-1]+self.fd*math.sin(self.omegad*self.t[-1]))*self.dt
            self.omega.append(temp_omega)
            temp_theta=self.theta[-1]+temp_omega*self.dt
            self.theta.append(temp_theta)
            temp_t=self.t[-1]+self.dt
            self.t.append(temp_t)
    def pendulum1(self):
        self.t=[0]
        while self.t[-1]<=self.total_time:
            temp_omega1=self.omega1[-1]+(-9.8/self.l*math.sin(self.theta1[-1])-self.q*self.omega1[-1]+self.fd*math.sin(self.omegad*self.t[-1]))*self.dt
            self.omega1.append(temp_omega1)
            temp_theta1=self.theta1[-1]+temp_omega1*self.dt
            self.theta1.append(temp_theta1)
            temp_t=self.t[-1]+self.dt
            self.t.append(temp_t)
    def cal_d_theta(self):
        while self.t[-1]<=self.total_time:
            temp_omega=self.omega[-1]+(-9.8/self.l*math.sin(self.theta[-1])-self.q*self.omega[-1]+self.fd*math.sin(self.omegad*self.t[-1]))*self.dt
            self.omega.append(temp_omega)
            temp_theta=self.theta[-1]+temp_omega*self.dt
            self.theta.append(temp_theta)       
            temp_omega1=self.omega1[-1]+(-9.8/self.l*math.sin(self.theta1[-1])-self.q*self.omega1[-1]+self.fd*math.sin(self.omegad*self.t[-1]))*self.dt
            self.omega1.append(temp_omega1)
            temp_theta1=self.theta1[-1]+temp_omega1*self.dt
            self.theta1.append(temp_theta1)
            self.d_theta.append(math.log(math.fabs(temp_theta-temp_theta1)))
            temp_t=self.t[-1]+self.dt
            self.t.append(temp_t)  
    def show_result(self):
        pl.plot(self.t,self.theta)
        pl.xlabel("time($s$)")
        pl.ylabel("angle($radians$)")
    def show_result1(self):
        _plot,=pl.plot(self.t,self.theta1)
        pl.xlabel("time($s$)")
        pl.ylabel("angle($radians$)")
        pl.legend([_plot],["initial_theta=0.2-0.001"])
    def show_result2(self):
        pl.plot(self.t,self.d_theta)
        pl.xlabel("time($s$)")
        pl.ylabel("log(d_theta)($radians$)")
a=chaotic_pendulums()
a.pendulum()
a.show_result()
b=chaotic_pendulums()
b.pendulum1()
b.show_result1()
c=chaotic_pendulums()
c.cal_d_theta()
c.show_result2()
z=np.polyfit(c.t,c.d_theta,1)
p=np.poly1d(z)
print(z)
print(p)

结论

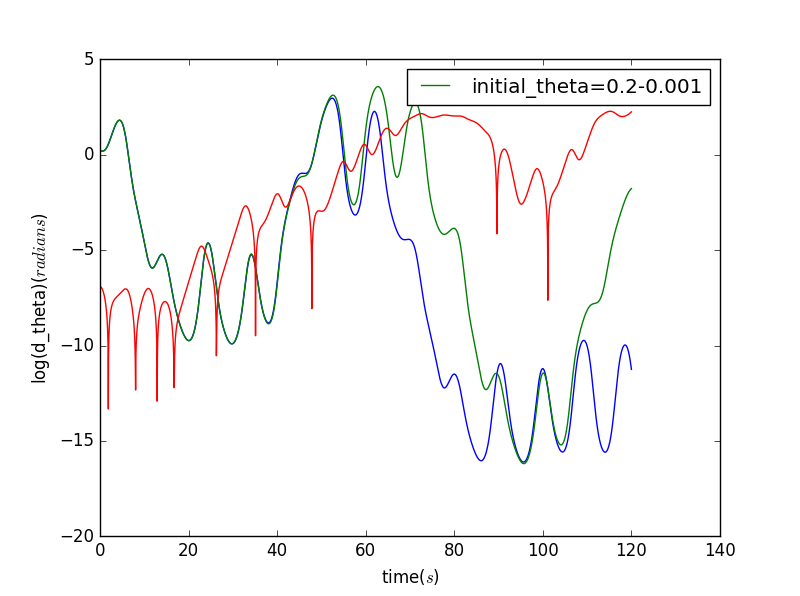
Lyapunov指数为0.08508

致谢

感谢秦大粤同学的分享!