第五次作业

---

作业2.6

---

摘要

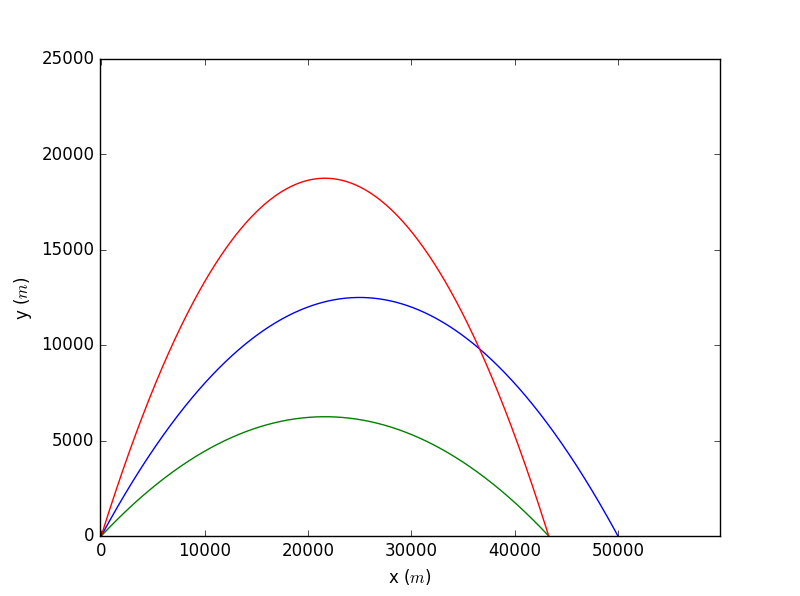
本次作业要求使用欧拉法研究炮弹的运动轨迹（忽略空气阻力）。

---

背景

题目原文：
2.6：Use the Euler method to calculate cannon shell trajectories ignoring both air drag and effect of air density (actually,ignoring the former automatically rules out the latter).Compare your results with those in Figure 2.4,and with the exact solution.

---

正文

忽略空气阻力时，炮弹的运动方程由牛顿第二定律可得：

$$\frac{d^2x}{dt^2}=0$$ $$\frac{d^2y}{dt^2}=-g$$
可以将方程组化为一阶微分方程：
$$\frac{dx}{dt}=v_x$$ $$\frac{dv_x}{dt}=0$$ $$\frac{dy}{dt}=v_y$$ $$\frac{dv_y}{dt}=-g$$
用欧拉法可以得到：
$$x_{i+1}=x_i+v_{x,i}Δt$$
$$v_{x,i+1}=v_{x,i}$$
$$y_{i+1}=y_i+v_{y,i}Δt$$
$$v_{y,i+1}=v_{y,i}-gΔt$$
即为炮弹的运动轨迹。

代码如下：

import pylab
from math import cos
from math import sin
from math import pi
class Euler2Dsimulation:
    def __init__(self,speed,theta,timestep=0.001):
        self._timestep=timestep
        self._x=[0]
        self._y=[0]
        self._vx=[speed*cos(theta)]
        self._vy=[speed*sin(theta)]
        self.g=9.8
        self.calculate()
        self.plot()
    def _accelerate(self,x,y,vx,vy):
        ansax=0
        ansay=-self.g
        return (ansax,ansay)
    def calculate(self):
        while self._y[-1]>=0:
            self._x.append(self._x[-1]+self._vx[-1]*self._timestep)
            self._y.append(self._y[-1]+self._vy[-1]*self._timestep)
            (ax,ay)=self._accelerate(self._x[-1],self._y[-1],self._vx[-1],self._vy[-1])
            self._vx.append(self._vx[-1]+self._timestep*ax)
            self._vy.append(self._vy[-1]+self._timestep*ay)
    def plot(self):
        pylab.plot(self._x, self._y)
        pylab.xlabel('x ($m$)')
        pylab.ylabel('y ($m$)')
Euler2Dsimulation(700,pi/4)
Euler2Dsimulation(700,pi/6)
Euler2Dsimulation(700,pi/3)
pylab.show()

结论

---

致谢

感谢曹昕宇同学跟我讲解。