Study-Note: Soft + Hardwired Attention : An LSTM Framework for Human Trajectory Prediction and Abnormal Event Detection

Study-Note OPTIMAL

---

中文理解

首先，作者利用轨迹的起点和终点(source and sink position)将数据集场景中的轨迹进行聚类，

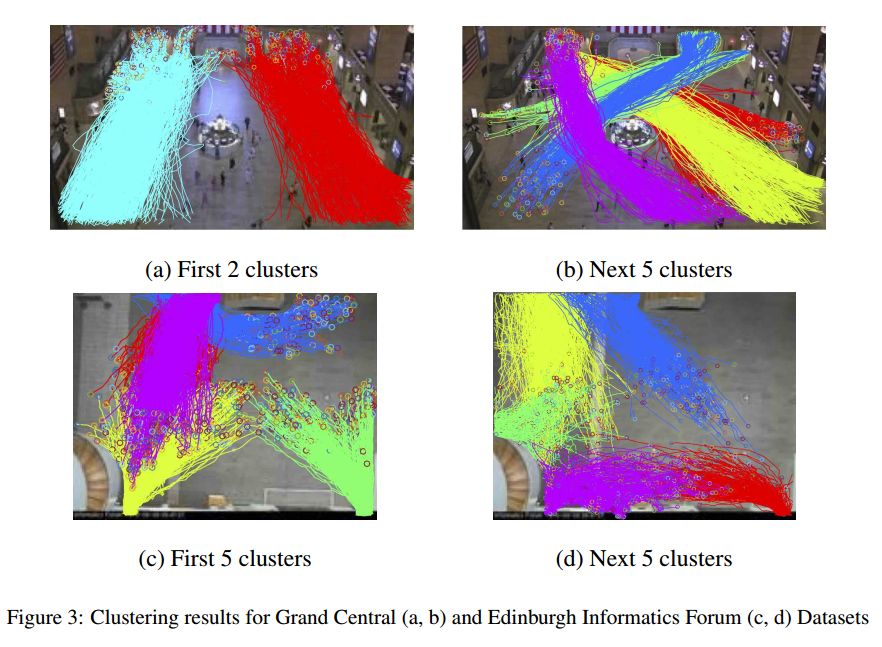
将人群分类后，对每一个类别训练不同的参数创建对应的轨迹模型。

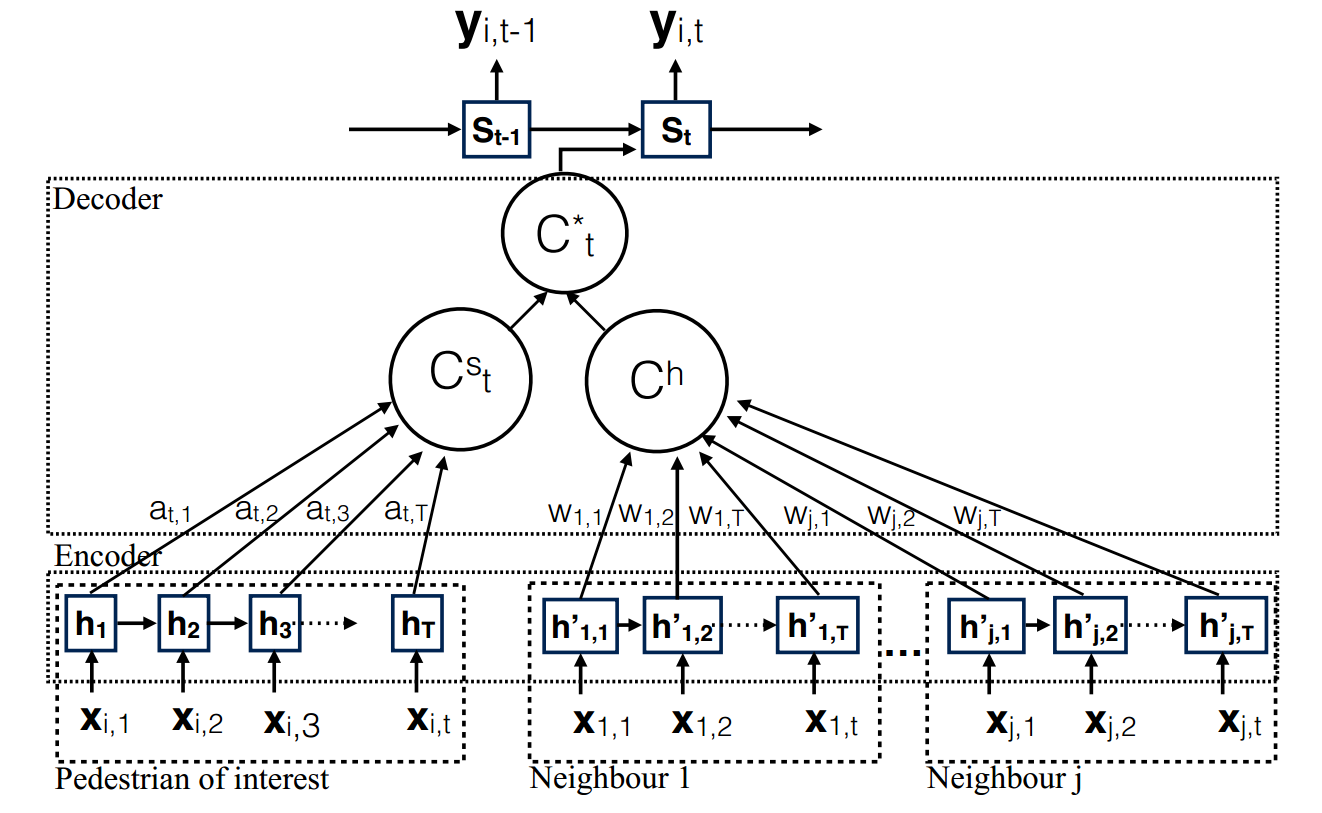
作者的模型可以用上图来描述。首先使用LSTM encoder对当前时刻 $T$ 之前$1 \rightarrow T$ 的轨迹点信息进行encoder，并获得相应的状态信息$h_1 \rightarrow h_T$，然后使用注意力机制将每一个轨迹的信息再做一次聚合，对当前要预测的这个人使用软性注意力聚合(soft attention)，即其系数$\alpha$由feed forward network $\left\{ \begin{array}{lr} \alpha_{tj} = \frac {\exp(e_{tj})} {\sum_{k=1}^T\exp(e_{tk})} & \\ \\ e_{tj} = a(s_{t-1}, h_j) & \end{array} \right.$ 结合预测系统得到；而对于其周围的人的系数$w$则根据距离这一硬性注意力(hardwired attention)聚合($w_{(n, j)} = \frac 1 {dist(n, j)}$)得到。再通过一个全连接层将两种聚合产物($C^s_t 和 C^h$)聚合为$C_t^*$作为LSTM Decoder的输入，通过LSTM Decoder解析出预测的路径。

Abstract

we propose a novel method to predict the future motion of a pedestrian given a short history of their, and their neighbours, past behaviour. The novelty of the proposed method is the combined attention model which utilises both “soft attention” as well as “hard-wired” attention in order to map the trajectory information from the local neighbourhood to the future positions of the pedestrian of interest.

Introduction

The approach we present in this paper can be viewed as a data driven approach which learns the relationship between neighbouring trajectories in an unsupervise manner.

Problem Definition

The task we are interested in is predicting the trajectory of the $i^{th}$ pedestrian for the period of $T_{obs+1}$ to $T_{pred}$, having observed the trajectory of the $i^{th}$ pedestrian from time $1$ to $T_{obs}$ as well as the trajectories all the other pedestrians in the local neighbourhood during that period.

Proposed Solution

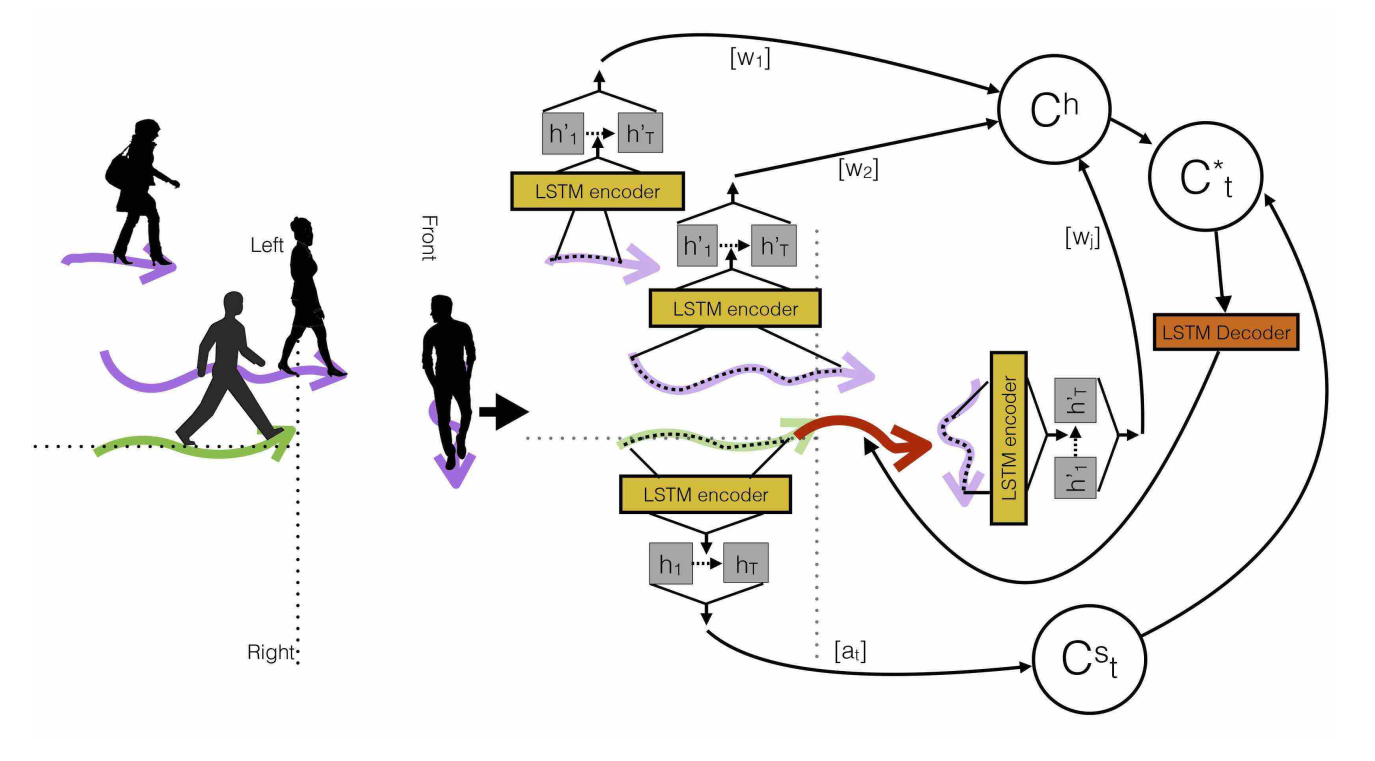
A sample surveillance scene (on the left): The trajectory of the pedestrian of interest is shown in green, and has two neighbours (shown in purple) to the left, one in front and none on right.

Neighbourhood encoding scheme (on the right): Trajectory information is encoded with LSTM encoders. A soft attention context vector $C_t^s$ is used to embed the trajectory information from the pedestrian of interest, and a hardwired attention context vector $C^h$ is used for neighbouring trajectories. In order to generate $C_t^s$ we use a soft attention function denoted $a_t$ in the above figure, and the hardwired weights are denoted by $w$. The merged
context vector is then used to predict the future trajectory for the pedestrian of interest (shown in red).

Proposed Approach

LSTM encoder-decoder Framework

The proposed Soft+Hardwired Attention model

We utilise the trajectory information from both the pedestrian of interest and the neighbouring trajectories. We embed the trajectory information from the pedestrian of interest with the soft attention context vector $C_t^s$, while neighbouring trajectories are embedded with the aid of a hardwired attention context vector $C_h$. In order to generate $C_t^s$ we use a soft attention function denoted $a_t$ in the above figure, and the hardwired weights are denoted by $w$. Then the merged context vector, $C_t^∗$, is used to predict the future state $y_i(t)$

LSTM Encoder

The input sequence for the pedestrian $i$ is given by

$$x_i = [x_1, y_1, \cdots, x_{T_{obs}}, y_{T_{obs}}]$$

The encoded sequence is given by,

$$h_i = [h_1, \cdots, h_T]$$

The encoding function is an LSTM, which can be denoted by,

$$h_t = LSTM(x_t, h_{t-1})$$

With the aid of above equation we encode tge trajectory information from hte pedestrian of interest as well as each trajectory in the local neighbourhood.

LSTM Decoder

The soft attention context vector $C_t^s$ can be computed as a weighted sum of hidden states,

$$C_t^s = \sum_{j=1}^{T_{obs}}\alpha_{tj}h_j$$

The weight $\alpha_{tj}h_j$ can be computed by,

$$\left\{ \begin{array}{lr} \alpha_{tj} = \frac {\exp(e_{tj})} {\sum_{k=1}^T\exp(e_{tk})} & \\ \\ e_{tj} = a(s_{t-1}, h_j) & \end{array} \right.$$
the function $a()$ is a feed forward network for joint training with other components of the system.

Let there be $N$ neighbouring trajectories in the local neighbourhood and $h'_{(n, j)}$ be
the encoded hidden state of the $n^{th}$ neighbour at the $j^{th}$ time instance, then the context vector for the hardwired attention model is defined as,

$$C^h = \sum_{n=1}^N\sum_{n=1}^{T_{obs}}w_{(n, j)}h'_{(n, j)}$$

The simplest repesentation scheme can be given by,

$$w_{(n, j)} = \frac 1 {dist(n, j)}$$ where $dist(n, j)$ is the distance between the $n^{th}$ neighbour and the pedestrian of interest at the $j^{th}$ time instance.

We then employ a simple concatenation layer to combine the information from individual attentions. Hence the combined context vector can be denoted as,

$$C_t^* = \tanh(W_c[C_t^s; C^h])$$ where $W_c$ is refered to as the set of weights for concatenation.We learn this weight value also through back-propagation.

The final prediction can be computed as,

$$y_t = LSTM(s_{t-1}, y_{t-1}, C_t^*)$$

Model learning

The given input trajectories in the training set are clustered used DBSCAN based on source and sink positions and we run an outlier detection algorithm for each cluster considering the entire trajectory.

In the training phase trajectories are clustered based on the entire trajectory and after clustering we learnt a separate trajectory prediction model for each generated cluster. When modelling the local neighbourhood of the pedestrians of interest, we have encoded the trajectories of those closest 10 neighbours in each direction, namely 165 front, left and right.

To select the appropriate prediction model to use, the mean trajectory for each cluster for the period of $1$ to $T_{obs}$ is generated and in the testing phase, the given trajectories are assigned to the closest cluster centre while considering those mean trajectories as the cluster centroids.

Comparison to the Social-LSTM model

1. The proposed combined attention model considers the entire sequence of hidden states for both the pedestrian of interest and his or her neighbours
2. Then we utilise time dependent weights which enables us to vary their influence in a timely manner.
3. Learning a different trajectory prediction model for each trajectory cluster.

Experiments

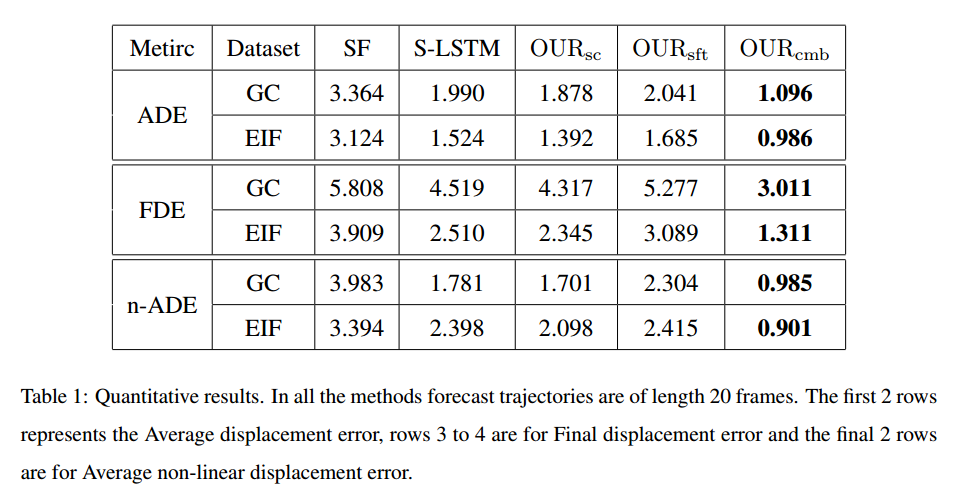
For the SF model, preferred speed, destination, and social grouping factors are used to model the agent behaviour.

For S-LSTM model a local neighbourhood of size 32px was considered and the hyper-parameters were set according to Alahi et al(2016).

In order to evaluate the strengths of the proposed model, we compare this combined attention model (OURcmb) and two variations on our proposed approach: 1) OURsft, 265 which ignore the neighbouring trajectories and considers only the soft attention component derived from the trajectory of the person of interest when making predictions; and 2) OURsc which omits the clustering stage such that only a single model (using combined attention weights) is learnt