Study Note : Pedestrian Behavior Understanding and Prediction with Deep Neural Networks

Study-Note 机器学习 OPTIMAL

---

原文 ： Pedestrian Behavior Understanding and Prediction with Deep Neural Networks

---

建立了一种Behavior-CNN模型，将一个场景中行人的前一半路径作为输入，输出（预测）其后一半的路径。

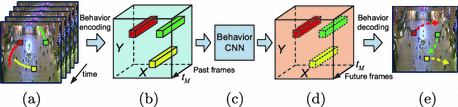
如上图， 其路径信息用一种特殊的编码方式将固定场景内所有人在一段时间内的运动轨迹信息集成到一个 $\mathcal{D} \in X \times Y \times 2M$ 的volume当中，传入Behavior-CNN, 输出预测的volume, 再 decoding出预测的未来的路径信息。

重点有两个，一是路径的编码方式， 如下 ：

1. 首先提取先前连续的M个时间点路径信息 $t_1, \dots, t_m$

2. 得到第i个行人在第m个时间点的空间位置信息 $l_i^m , m \in [1, M]$

   • 假设 $p_1, ..., p_N$是场景中的N个人
   • $t_1, ..., t_M$ 是M个均匀采样的时间点，$t_m$ 是当前时间点
   • $p_i$在时间点$m$的归一化的空间位置信息为 $l_i^m = [x_i^m / X, y_i^m /Y]$，其中$x_i^m \in [1, X]$和$y_i^m \in [1, Y]$是$p_i$在时间点$t_m$的空间坐标， $[X, Y]$ 是数据帧的大小。

3. 对每个行人$p_i$的空间位置信息处理得到出一个2M维的位移向量

   行人$p_i$基于时间点$t_m$在过去的M帧里的位移向量(displcement vector)为：
   

   $$d_i = [l_i^M - l_i^1, l_i^M - l_i^2, ..., l_i^M - l_i^{M-1}, l_i^M - l_i^M]^T \in \mathbb{R}^{2M}$$

4. 将场景内N个人的位移向量集成到一个volume $\mathcal{D} \in \mathbb{R}^{X \times Y \times 2M}$ 中。 $D(x_i^M, y_i^M, :) = d_i + 1^T$，使得$d_i$从 $(-1, 1)$转移到 $(0, 2)$的范围。

第二个重点是Behavior-CNN的investigations :

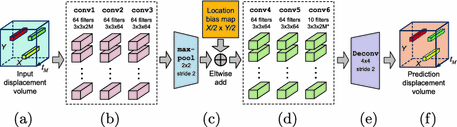
1. 输入和输出均为displacement volume $\mathcal{D}$ （a, f）

   输入集成了前半段$t_1, ... t_M$总共M个时间场景中行人的运动轨迹信息，输出是后半段$t_{M+1}, ..., t_{M + M^*}$ 的预测轨迹运动信息

2. 3个底层的卷积层（b）

   conv1 有64个大小为 $3 \times 3 \times 3 \times 2M$ 的filter , 而 conv2 and conv3 各有64个大小为 $3 \times 3\times 64$的filter.

   bottom convolution layers的作用是，提取输入的信息根据行人行为将不同的行人分成多个类。假设训练后的conv1的某一个filter对输入的信息有很高的response，则当前volume中的新人可能会倾向于向场景的左下部分移动，对另外某一个filter有response，则会倾向于向场景的右上方移动

3. 一个max-pooling层引入对少量平移的不变性, 感受野（receptive field）的范围也会加倍

4. location bias map用于自动学习场景的布局信息，如障碍等
5. 3个高层的卷积层，用于编码更加复杂的行人行为

实验比较了Behavior-CNN和一系列其他算法，效果均比其他模型更好。

---

Contribution

1. Longterm pedestrian behaviors is modeled with deep CNN. In-depth investigations on the proposed Behavior-CNN is conducted on
   
   • the learned location map
   • the location awareness property
   • semantic meaning of learned filters
   • the influence of receptive fields on behavior modeling
2. A pedestrian behavior encoding scheme is proposed to encode pedestrian walking paths into sparse displacement volumes, which can be directly used as input/output for deep networks without association ambiguities.
3. The effectivencess of Behavior-CNN is demonstrated through applications on path prediction, destination prediction, and tracking.

Pedestrian Behavior Modeling and Prediction

Overall Framework

（a）. Pedestrian walking paths in previous frames.
（b）. Displacement volume encoded from pedestrians' past walking path in (a)
（c）. Behavior-CNN
（d）. The predicted displacement volume by Behavior-CNN
（e）. Predicted future pedestrian walking path decoded form (d)

Pedestrian Walking Behavior Encoding

（a）. Pedestrian walking paths in the previous $M$ time points, $t_1, ..., t_M$
（b）. Spatial locations of each person at these time piunts, $l_i^m$ and $l_j^m$ for $m \in [1, M]$

• let $p_1, ..., p_N$ be $N$ pedestrians in a scene
• $t_1, ..., t_m$ be $M$ uniformly sampled time points to be used as input for behavior encoding, and $t_M$ be the current time point.
• The normalized spatial location of $p_i(i \in [1, N])$ at time point $t_m(m \in [1, M])$ is denoted as $l_i^m = [x_i^m / X, y_i^m / Y]$, where $x_i^m \in [1, X], y_i^m \in[1, Y]$ are the spatial coordiate of $p_i$ at time $t_m$, and $[X, Y]$ is the spatial size of the input frame.

（c）. Computed $2M$-dimensional displacement vector $d_i$ and $d_j$ for pedestrians $i$ and $j$.

A 2M-dimensional displacement vector $d_i = [l_i^M - l_i^1, l_i^M - l_i^2, ..., l_i^M - l_i^{M-1}, l_i^M - l_i^M]^T \in \mathbb{R}^{2M}$ is used to describe pedestrian $p_i$'s walking path in the past $M$ frames with respect to $t_M$

（d）. Encoded displacement volume $\mathcal{D}$ combined from displacement vectors of all pedestrians in the scene.

The input of CNN is constracted as a 3D displacement volume $\mathcal{D} \in \mathbb{R}^{X \times Y \times }$ based on $d_i$.

For each pedestrian $p_i$, all the 2M channels of $\mathcal{D}$ at $p_i$'s current location $(x_i^M, y_i^M)$ are assigned with the displacement vector $d_i$.

$D(x_i^M, y_i^M, :) = d_i + 1^T$, where $1^T$ represents a all-one vector. All the remaining entries of $\mathcal{D}$ are set as zeros.

Behavior-CNN

（a）. An input displacement volume $\mathcal{D}$
（f）. An output displacement volume $\mathcal{D}^*$

Behavior-CNN takes the displacement volume $\mathcal{D} \in \mathbb{R}^{X \times Y \times 2M}$ as input， and predict future displacement volume ($\mathcal{D}^* \in \mathbb{R}^{X \times Y \times 2M}$) as output. $t_1, ..., t_M$ are $M$ previous time points, and $t_{M+1}, ..., t_{M + M^*}$ are $M^*$ future time points to predict.

（b）. Three bottom convolution layers

conv1 contains 64 filters of size $3 \times 3 \times 3 \times 2M$, while both conv2 and conv3 contain64 filters of size $3 \times 3\times 64$

（c）. A max-pooling layer and an elementwise addition layer that adds a learnable bias to each location of the feature maps.

The three bottom convolution layers are followed by max pooling layer max-pool with stride 2.

A learnable location bias map of size $X/2 \times Y/2$ is channel-wisely added to each of the pooled feature maps. Every location has one independent bias value shared across channels. With the bias map, location information fo the scene can be automatically learned by the proposed Behavior-CNN.

（d）. Three top convolution layers.

As for the three top convolution layers, conv4 and conv5 contain 64 filters of size $3 \times 3 \times 3 \times 64$, while conv6 contains 2M* filters of size $3 \times 3 \times 3 \times 64$ to output the predicted displacement volume.

（e）. A deconvolution layer.

A deconvolution layer is used to upsample the output prediction of conv6 to the same spatial size as the input displacement volume.

Loss Function

the loss function of Behavior-CNN is defined as the averaged squared $L_2$ distance between the predicted displacement volume $\widehat{\mathcal{D}^*}$ and the ground truth output displacement volume $\mathcal{D}^*$ on all the valid (non-zero) entries of $D^*$.

$$Loss = \frac 1 {\sum\mathcal{M}} \|(\widehat{\mathcal{D}^*} - \mathcal{D}^*) \circ \mathcal{M}\|_2^2$$

• $\circ$ is the Hadamard product operator
• $\mathcal{M}$ is a binary mask. $\mathcal{M}$ is $1$ for the entries where $\mathcal{D}^*$ is non-zero, while $\mathcal{M}$ is 0 for the entires where $\mathcal{D}^*$ is zero.
• $\sum\mathcal{M}$ counts the total number of non-zeros entries of $\mathcal{M}$ for normalization.

Trianing Schemes

Two strategies to obtain the training sample of pedestrian walking paths.

• The annotated pedestrian locations are first used for both model training and evalution to investigate the propeties of learne behavior-CNN.
• in order to handle real-world scenarios, our model is also trained with keypoint tracking results by the KLT tracker while the human annotations are only used for evaluation.

Due to the high sparsity, we prefer a layer-by-layer training strategy to training all the parameters together.
A simpler network with three convolution layers is first randomly initialized and trained until convergence.
Afterwards, the trained convolution layers are used as the bottom layers of Behavior-CNN.The following layers are then appended and parameters of the newly added layers are trained from random initialization.Lastly, all the layers are jointly fine-tuned.

Stochasic gradient descent is adopted for training and the model converged at around 10k iterations.

Data and Evaluation

Data

• Pedestrian Walking Route Dataset -- 4,000s in length and 12684 pedestrians are annotated.
• The complete trajectories of 797 pedestrians from the time point he/she enters the scene to the time he/she leaves are annotated every 20 frames.

Evaluation Metric

Mean squared error(MSE) is adopted as the evaluation metric for the task of pedestrian walking path prediction.

$$MSE = \frac 1 {NM^*} \sum_{i = 1}^N\sum_{m = 1}^{M^*} \|l_i^{M + m} - \widehat{l_i}^{M + m}\|_2 \times 100 \%$$

$\widehat{l_i}^{M + m} = [x_i^{M + m} / X, y_i^{M + m} / Y]$ is the normalized location of p_i at time t_{M + m} with respect to the size of the scene.

Investigations on Behavior-CNN

Investigation on location awareness of Behavior-CNN.

With the learned locaiton bias map, our learned model is able to capture the location information and scene layout from the input pedestrian walking paths.

Learned Feature Filters of Behavior-CNN

The three bottom convolution layers conv1-3) takes all the pedestrian behaviors as input and gradually classify them into finer and finer categories according to various criteria. In top layers, the influences of all different categories are combined together to generate the prediction.

Receptive Fields

Pedestrian walking behaviors are significantly influenced by nearby pedestrians. By increasing the size of the receptive field, the sensing range of the network can be increased and the pedictions are more reliable.

Application

Pedestrian Destination Prediction

By encoding the output displacement volume and re-encoding the prediction results, the predicted walking paths can be fed back into Behavior-CNN as input. In this way, long-term walking paths can be recurrently preficted. The long-term prediction results can be used for destination prediction.

Predictions as Tracking Prior

Using KLT tracker as a basline tracking algorithm to be improved.

Given successfully tracked locations(up to the failing time) as input, $M^* = 5$ future location (4s) can be predicted by Behavior-CNN. Then the tracklet that baset matches prediction is selected to be connected with the fragmented tracklet.

拓展阅读

• KLT tracker 方法： Tomasi, C., Kanade, T.: Detection and tracking of point feature
• MDA方法 ： Zhou, B., Wang, X., Tang, X.: Understanding collective crowd behaviors: learning a mixture model of dynamic pedestrian-agents
• UVP 方法： Walker, J., Gupta, A., Hebert, M.: Patch to the future: unsupervised visual prediction.
• EMM 方法： Yi, S., Li, H., Wang, X.: Understanding pedestrian behaviors from stationary crowd groups.