ISYE 6412 HW #1

Name: Haoming Jiang

Problem #1

(a)

$S$: $\mathbb{R}$
$\Omega$: normal distribution with variace 1 ad mean $\theta, \theta\in\mathbb{R}$
$D$: $d \in\mathbb{R}$
$L$: $\frac{(\theta-d)^2}{(1+\theta^2)}$

(b)

for $\delta = a+bX$, $R_{\delta}(\theta) = E_\theta(\frac{(\theta - d)^2}{1+\theta^2}) = E_\theta(\frac{((1-b)\theta - a-b(X-\theta))^2}{1+\theta^2})= \\E_\theta(\frac{((1-b)\theta - a)^2+b^2(X-\theta)^2 - 2((1-b)\theta - a)(X-\theta)}{1+\theta^2})$
with the fact that $E_\theta(X) = \theta, Var_\theta(X) = 1$
$R_{\delta}(\theta) = \frac{((1-b)\theta - a)^2 + b^2}{1+\theta^2}$

$R_{\delta_1}(\theta) = \frac{1}{1+\theta^2}$
$R_{\delta_2}(\theta) = \frac{0.25\theta^2+0.5-0.5\theta}{1+\theta^2}$
$R_{\delta_3}(\theta) = \frac{0.25+0.25\theta^2}{1+\theta^2} = 0.25$
$R_{\delta_4}(\theta) = \frac{\theta^2+4}{1+\theta^2}$
$R_{\delta_5}(\theta) = \frac{\theta^2}{1+\theta^2}$
$R_{\delta_6}(\theta) = \frac{(\theta-1)^2}{1+\theta^2}$

(c)

Yes $\delta_4$ is inadmissible, sine $R_{\delta_5}(\theta) < R_{\delta_6}(\theta)$

(d)

$\delta_1$, because $E_\theta(\delta_1(X)) = \theta$

(e)

$R_{\delta_{1,n}}(\theta) = E_\theta(\frac{(\theta - \bar{X}_n)^2}{1+\theta^2}) = \frac{(1/n)}{1+\theta^2}$

$R_{\delta_{2,n}}(\theta) = E_\theta(\frac{(\theta - \frac{\bar{X}_n+n^{-1}}{1+n^{-1}})^2}{1+\theta^2}) = E_\theta(\frac{(\frac{(\bar{X}_n - \theta)+n^{-1}(1-\theta)}{1+n^{-1}})^2}{1+\theta^2}) = \frac{ (1-\theta)^2 + n }{(1+\theta^2)*(1+n)^2}$

$R_{\delta_{3,n}}(\theta) = E_\theta(\frac{(\theta - \frac{\sqrt{n}\bar{X}_n}{1+\sqrt{n}})^2}{1+\theta^2}) = E_\theta(\frac{(\ \frac{\sqrt{n}(\bar{X}_n-\theta)- \theta}{1+\sqrt{n}})^2}{1+\theta^2}) = \frac{\theta^2+1}{(1+\theta^2)*(1+\sqrt{n})^2} = \frac{1}{1+\sqrt{n}}^2$

$R_{\delta_{6,n}}(\theta) = E_\theta(\frac{(\theta - 1)^2}{1+\theta^2}) = \frac{(\theta - 1)^2}{1+\theta^2}$

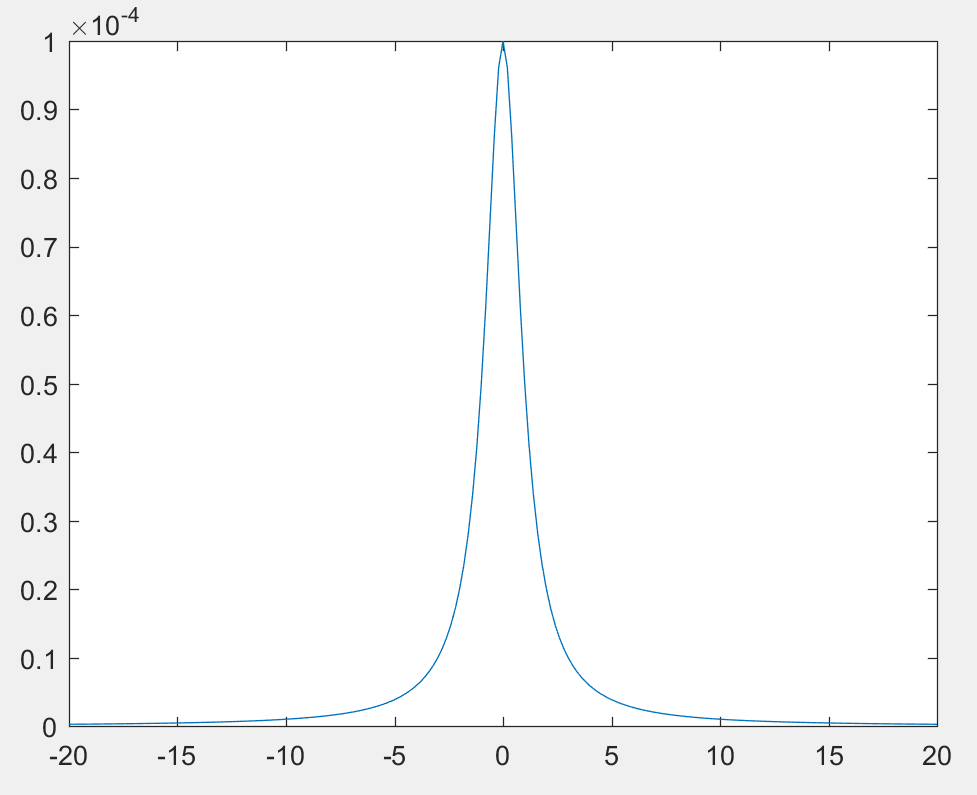
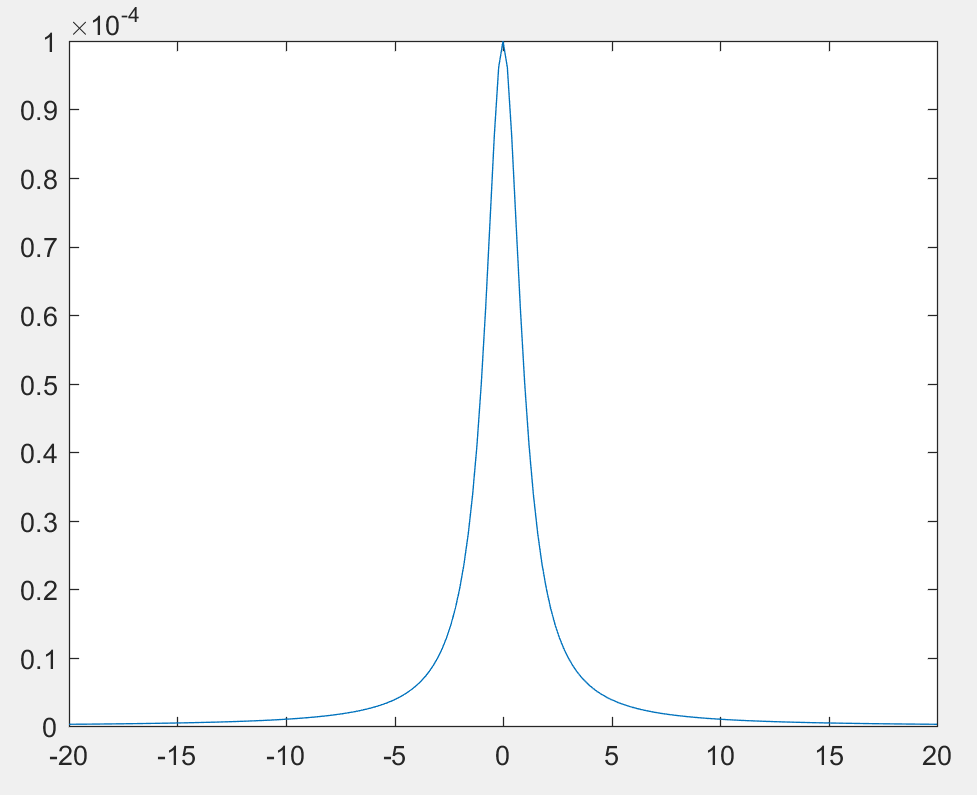
(f)

I would like to use $\delta_{3,n}$. Since for any $\theta$, the risk is the same and converge to 0, when n goes to infinity.

(g)

$R_{\delta_{a,b,n}}(\theta) = E_\theta(\frac{(\theta - a-b\bar{X}_n)^2}{1+\theta^2}) = E_\theta(\frac{(\theta - a-b\theta-b(\bar{X}_n-\theta))^2}{1+\theta^2}) = \frac{(\theta(1-b)-a)^2+b^2/n}{1+\theta^2}$

When $|\theta|\rightarrow \infty$, $R_{\delta_{a,b,n}}(\theta) \rightarrow (1-b)^2 = 0$ if and only if $b=1$

With $b=1$, $R_{\delta_{a,b,n}}(\theta) = \frac{a^2+b^2/n}{1+\theta^2}$, so the choice $a=0$ gives uniformly smallest risk function.

(h)

when $\theta = 1$, $R_{\delta_{6,n}}(1)=0$. As a result for any $\delta'$ which is better than $\delta_{6,n}$, $R_{\delta'}(1)=0$. Which means $E_\theta(\frac{(\delta_{6,n}(X_1,...,X_n)-1)^2}{1+1^2}) = 0$. So $\delta_{6,n}(X_1,...,X_n) \equiv 1$. So $\delta_{6,n}$ is admissible.

Problem #2

(a)

$S$: $\mathbb{Z}$
$\Omega$: binomial distribution with parameter $\theta \in [0,1]$
$D$: $d \in [0,1]$
$L$: $L(\theta,d) = |\theta-d|$

(b)

$R_{\delta_{1}}(\theta) = E_\theta(|\theta-\frac{X}{20}|) = \sum_{i=0}^{20}(C_{20}^i\theta^i(1-\theta)^{n-i}|\theta-\frac{i}{20}|)$
$R_{\delta_{2}}(\theta) = E_\theta(|\theta-\frac{1}{4}|) = |\theta-\frac{1}{4}|$
$R_{\delta_{3}}(\theta) = E_\theta(|\theta-1|) = |\theta-1|$

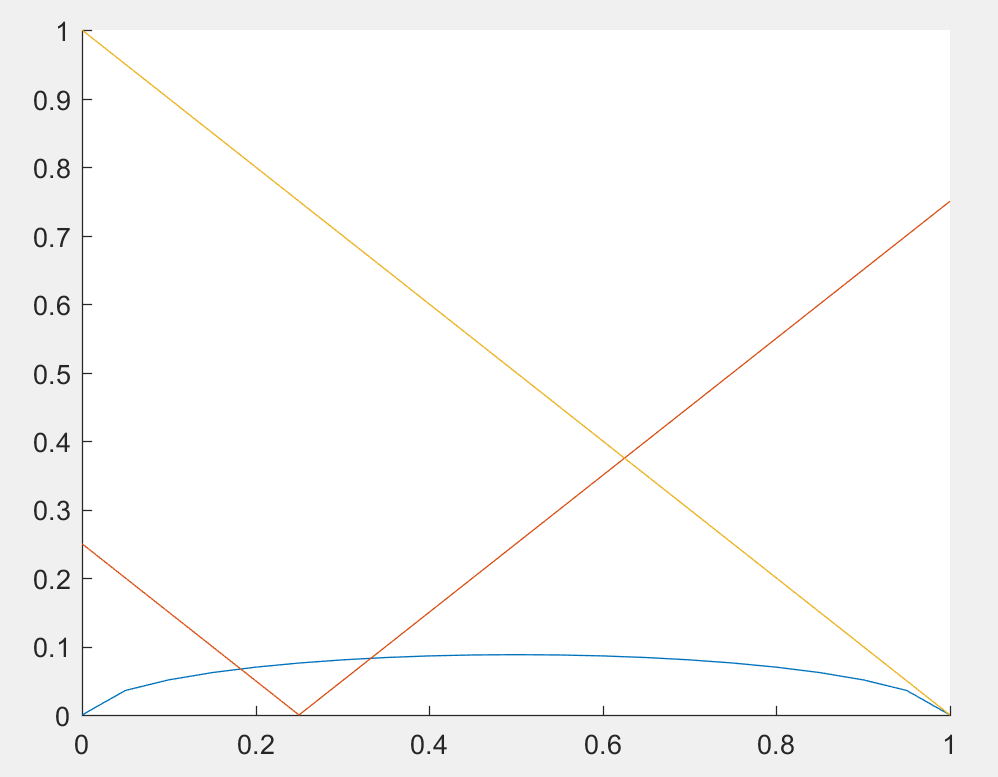
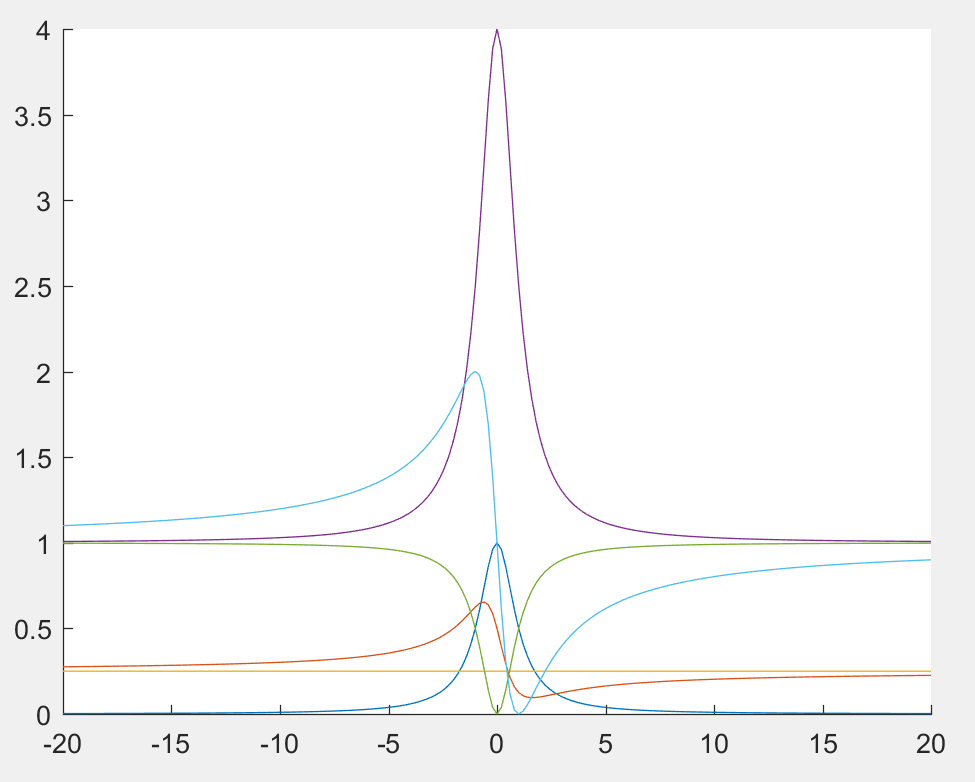
blue line is $\delta_1$
red line is $\delta_2$
yellow line is $\delta_3$

(c)

If there exits another procedure $\delta'$, s.t. $R_{\delta'} (\theta) \leq R_{\delta_2}(\theta), for\ \theta \in [0,1]$.

As a result $0 \leq R_{\delta'} (1/4) \leq R_{\delta_2}(1/4) = 0$
So $E_{1/4}(|\delta'(X)-1/4|) = 0$. Which means, $|\delta'(X)-1/4| \equiv 0$. As a result $\delta'(X) = \delta_2(X)$. So $\delta_2(X)$ is admissible.

(d)

When n = 2, If there exits another procedure $\delta'$, s.t. $R_{\delta'} (\theta) \leq R_{\delta_3}(\theta), for\ \theta \in [0,1]$.

As a result $|\delta'(0)-\theta|*(1-\theta)^2 + |\delta'(1)-\theta|*2(1-\theta)\theta + |\delta'(2)-\theta|*\theta^2 \\ \leq 1-\theta$.

When $\theta=1$, $|\delta'(2)-1| \leq 0$. So $\delta'(2)=1$.

So $|\delta'(0)-\theta|*(1-\theta)^2 + |\delta'(1)-\theta|*2(1-\theta)\theta \leq (1-\theta)^2*(1+\theta)$.
Let $\theta \rightarrow 1$. Both $|\delta'(0)-\theta|*(1-\theta)^2$ and $(1-\theta)^2*(1+\theta)$ converge to $0$ at the speed of $(1-\theta)^2$. So the inquality holds, if and only if $|\delta'(1)-\theta|*2(1-\theta)\theta$ also converges to 0 at the speed of $(1-\theta)^2$. As a result, $\delta'(1) = 1$.

So $|\delta'(0)-\theta|*(1-\theta)^2 \leq (1-\theta)^3$. Both sides are devided by $(1-\theta)^2$, and the extend defination to where $\theta = 1$ with the continuity. So $|\delta'(0)-\theta| \leq (1-\theta)$. So $\delta'(0)=1$.

So $\delta_3$ is addmissable.