在此处输入标题

作业

---

一、摘要

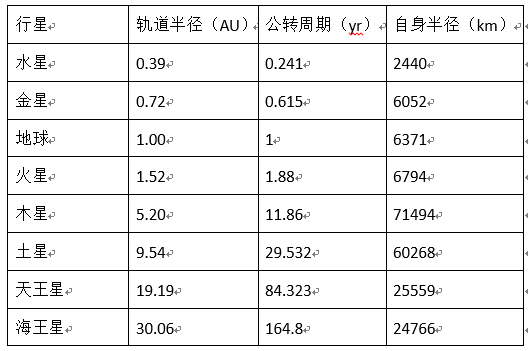
二、背景
Earth orbits the Sun,the equation is

$$F_{G}=\frac{GM_{S}M_{E}}{r^{2}}$$
From Newton's second law of motion we have $$\frac{\mathrm{d}^2 x}{\mathrm{d} t^{2}}=\frac{F_{G,x}}{M_{E}} ,\frac{\mathrm{d}^2 y}{\mathrm{d} t^{2}}=\frac{F_{G,y}}{M_{E}}$$
Using astronomical units,1AU is the average distance between the Sun and Earth.1 year is approximately $3.2\times 10^7s$,We find $$GM_{S}=4\pi ^4AU^3/yr^2$$
We new write each of the second-order differential equations as two first-order differential equations: $$v_{x,i+1}=v_{x,i}-\frac{4\pi ^2x_{i}}{r_{i}^3}\Delta t$$ $$x_{i+1}=x_{i}+v_{x,i+1}\Delta t$$ $$v_{y,i+1}=v_{y,i}-\frac{4\pi ^2y_{i}}{r_{i}^3}\Delta t$$ $$y_{i+1}=y_{i}+v_{y,i+1}\Delta t$$
If the force go as$1/r^{2.00000000001}$,the gravitational force is of the form $$F_{G}=\frac{GM_{S}M_{E}}{r^{\beta}}$$
The planets whose orbits deviate the most from circular are Mercury.The force law predicted by general relativity is $$F_{G}\approx \frac{GM_{S}M_{E}}{r^{2}}(1+\frac{\alpha }{r^{2}})$$
三、正文
1

import matplotlib.pyplot as plt
import numpy as np
import math
beta=[2.01,2.10,2.50,3.00]
x0=0
y0=0
class elliptical:
    def __init__(self,e=0.2,GMs=4*math.pi**2,dt=0.0001,time=4):
        self.e=e
        self.GMs=GMs
        self.x1=[1]
        self.y1=[0]
        self.vx1=[0]
        self.vy1=[2*math.pi*math.sqrt(1-self.e)]
        self.x2=[1]
        self.y2=[0]
        self.vx2=[0]
        self.vy2=[2*math.pi*math.sqrt(1-self.e)]
        self.x3=[1]
        self.y3=[0]
        self.vx3=[0]
        self.vy3=[2*math.pi*math.sqrt(1-self.e)]
        self.x4=[1]
        self.y4=[0]
        self.vx4=[0]
        self.vy4=[2*math.pi*math.sqrt(1-self.e)]
        self.dt=dt
        self.time=time
        self.r1=[math.sqrt(self.x1[0]**2+self.y1[0]**2)]
        self.r2=[math.sqrt(self.x2[0]**2+self.y2[0]**2)]
        self.r3=[math.sqrt(self.x3[0]**2+self.y3[0]**2)]
        self.r4=[math.sqrt(self.x4[0]**2+self.y4[0]**2)]
    def calculate(self):
        for i in range(int(self.time//self.dt)):
            self.vx1.append(self.vx1[i]-self.GMs*self.x1[i]*self.dt/self.r1[i]**(beta[0]+1))
            self.vy1.append(self.vy1[i]-self.GMs*self.y1[i]*self.dt/self.r1[i]**(beta[0]+1))
            self.x1.append(self.x1[i]+self.vx1[i+1]*self.dt)
            self.y1.append(self.y1[i]+self.vy1[i+1]*self.dt)
            self.r1.append(math.sqrt(self.x1[i+1]**2+self.y1[i+1]**2))
        for j in range(int(self.time//self.dt)):
            self.vx2.append(self.vx2[j]-self.GMs*self.x2[j]*self.dt/self.r2[j]**(beta[1]+1))
            self.vy2.append(self.vy2[j]-self.GMs*self.y2[j]*self.dt/self.r2[j]**(beta[1]+1))
            self.x2.append(self.x2[j]+self.vx2[j+1]*self.dt)
            self.y2.append(self.y2[j]+self.vy2[j+1]*self.dt)
            self.r2.append(math.sqrt(self.x2[j+1]**2+self.y2[j+1]**2))
        for i in range(int(self.time//self.dt)):
            self.vx3.append(self.vx3[i]-self.GMs*self.x3[i]*self.dt/self.r3[i]**(beta[2]+1))
            self.vy3.append(self.vy3[i]-self.GMs*self.y3[i]*self.dt/self.r3[i]**(beta[2]+1))
            self.x3.append(self.x3[i]+self.vx3[i+1]*self.dt)
            self.y3.append(self.y3[i]+self.vy3[i+1]*self.dt)
            self.r3.append(math.sqrt(self.x3[i+1]**2+self.y3[i+1]**2))
        for j in range(int(self.time//self.dt)):
            self.vx4.append(self.vx4[j]-self.GMs*self.x4[j]*self.dt/self.r4[j]**(beta[3]+1))
            self.vy4.append(self.vy4[j]-self.GMs*self.y4[j]*self.dt/self.r4[j]**(beta[3]+1))
            self.x4.append(self.x4[j]+self.vx4[j+1]*self.dt)
            self.y4.append(self.y4[j]+self.vy4[j+1]*self.dt)
            self.r4.append(math.sqrt(self.x4[j+1]**2+self.y4[j+1]**2))
    def show_results(self):
        ax1=plt.subplot(221)
        ax2=plt.subplot(222)
        ax3=plt.subplot(223)
        ax4=plt.subplot(224)
        plt.sca(ax1)
        plt.plot(self.x1,self.y1,label='trajectory')
        plt.scatter(x0,y0)
        plt.title(r'$\beta=2.01$'+ 'Simulation of elliptical orbit',fontsize=10)
        plt.xlabel(u'x(AU)',fontsize=10)
        plt.ylabel(u'y(AU)',fontsize=10)
        plt.sca(ax2)
        plt.plot(self.x2,self.y2,label='trajectory')
        plt.scatter(x0,y0)    
        plt.title(r'$\beta=2.10$'+ 'Simulation of elliptical orbit',fontsize=10)
        plt.xlabel(u'x(AU)',fontsize=10)
        plt.ylabel(u'y(AU)',fontsize=10)
        plt.sca(ax3)
        plt.plot(self.x3,self.y3,label='trajectory')
        plt.scatter(x0,y0)
        plt.title(r'$\beta=2.50$'+ 'Simulation of elliptical orbit',fontsize=10)
        plt.xlabel(u'x(AU)',fontsize=10)
        plt.ylabel(u'y(AU)',fontsize=10)
        plt.sca(ax4)
        plt.plot(self.x4,self.y4,label='trajectory')
        plt.scatter(x0,y0)    
        plt.title(r'$\beta=3.00$'+ 'Simulation of elliptical orbit',fontsize=10)
        plt.xlabel(u'x(AU)',fontsize=10)
        plt.ylabel(u'y(AU)',fontsize=10)
        plt.xlim(-1,1)
        plt.ylim(-1,1)
        plt.legend(fontsize=10,loc='best')
a=elliptical()
a.calculate()
a.show_results()
plt.show()

2

import matplotlib.pyplot as plt
import numpy as np
import math
alfa=0.0008
x0=0
y0=0
xp=[]
yp=[]
tp=[]
theta=[]
class elliptical:
    def __init__(self,GMs=4*math.pi**2,dt=0.0001,time=2):
        self.GMs=GMs
        self.x=[0.47]
        self.y=[0]
        self.vx=[0]
        self.vy=[8.2]
        self.dt=dt
        self.time=time
        self.r=[math.sqrt(self.x[0]**2+self.y[0]**2)]
        self.t=[0]
    def calculate(self):
        for i in range(int(self.time//self.dt)):
            self.vx.append(self.vx[i]-self.GMs*self.x[i]*self.dt/self.r[i]**3-alfa*self.GMs*self.x[i]*self.dt/self.r[i]**5)
            self.vy.append(self.vy[i]-self.GMs*self.y[i]*self.dt/self.r[i]**3-alfa*self.GMs*self.y[i]*self.dt/self.r[i]**5)
            self.x.append(self.x[i]+self.vx[i+1]*self.dt)
            self.y.append(self.y[i]+self.vy[i+1]*self.dt)
            self.t.append(self.t[i]+self.dt)
            self.r.append(math.sqrt(self.x[i+1]**2+self.y[i+1]**2))
    def precession(self):
        for j in range(len(self.r)-2):
            if (self.r[j+1]**2-self.r[j]**2>0 and self.r[j+1]**2-self.r[j+2]**2>0):
                xp.append(self.x[j+1])
                yp.append(self.y[j+1])
                tp.append(self.t[j+1])
                if self.x[j+1]>=0 and self.y[j+1]/self.x[j+1]>=0:
                    theta.append(math.atan(self.y[j+1]/self.x[j+1])*180/math.pi)
                if self.x[j+1]>=0 and self.y[j+1]/self.x[j+1]<0:
                    theta.append(math.atan(self.y[j+1]/self.x[j+1])*180/math.pi+360)
                if self.x[j+1]<0 and self.y[j+1]/self.x[j+1]>=0:
                    theta.append(math.atan(self.y[j+1]/self.x[j+1])*180/math.pi+180)
                if self.x[j+1]<0 and self.y[j+1]/self.x[j+1]<0:
                    theta.append(math.atan(self.y[j+1]/self.x[j+1])*180/math.pi+180)
    def show_results(self):
        for j in range(len(xp)):
            plt.plot([0,xp[j]],[0,yp[j]])
        plt.plot(self.x,self.y,'g',label=r'$\alpha$=0.0008'+' trajectory')
        plt.scatter(x0,y0)
        #plt.scatter(tp,theta,label='trajectory')
        plt.title(r'$\alpha$=0.0008'+'  Simulation of the precession of Mercury ',fontsize=14)
        plt.xlabel(u'x(AU)',fontsize=14)
        plt.ylabel(u'y(AU)',fontsize=14)
        #plt.xlabel(u'time(yr)')
        #plt.ylabel(u'$\Theta$(degrees)',fontsize=14)
        #plt.xlim(-1,1)
        #plt.ylim(-1,1)
        plt.legend(fontsize=14,loc='best')
a=elliptical()
a.calculate()
a.precession()
a.show_results()
plt.show()

3

import matplotlib.pyplot as plt
import numpy as np
import math
alfa=[0.0003,0.0005,0.0008,0.0015,0.0035]
xp=[[],[],[],[],[]]
yp=[[],[],[],[],[]]
tp=[[],[],[],[],[]]
theta=[[],[],[],[],[]]
xy=[[],[],[],[],[]]
x2=[[],[],[],[],[]]
x_mean=[]
y_mean=[]
xy_mean=[]
x2_mean=[]
xy1=[]
x21=[]
xf=np.linspace(0,2,200)
yf=[]
class elliptical:
    def __init__(self,GMs=4*math.pi**2,dt=0.0001,time=2):
        self.GMs=GMs
        self.x=[[0.47],[0.47],[0.47],[0.47],[0.47]]
        self.y=[[0],[0],[0],[0],[0]]
        self.vx=[[0],[0],[0],[0],[0]]
        self.vy=[[8.2],[8.2],[8.2],[8.2],[8.2]]
        self.dt=dt
        self.time=time
        self.r=[[math.sqrt(self.x[0][0]**2+self.y[0][0]**2)],[math.sqrt(self.x[0][0]**2+self.y[0][0]**2)],[math.sqrt(self.x[0][0]**2+self.y[0][0]**2)],[math.sqrt(self.x[0][0]**2+self.y[0][0]**2)],[math.sqrt(self.x[0][0]**2+self.y[0][0]**2)]]
        self.t=[[0],[0],[0],[0],[0]]
        self.a=[]
        self.b=[]
    def calculate(self):
        for n in range(len(alfa)):
            for i in range(int(self.time//self.dt)):
                self.vx[n].append(self.vx[n][i]-self.GMs*self.x[n][i]*self.dt/self.r[n][i]**3-alfa[n]*self.GMs*self.x[n][i]*self.dt/self.r[n][i]**5)
                self.vy[n].append(self.vy[n][i]-self.GMs*self.y[n][i]*self.dt/self.r[n][i]**3-alfa[n]*self.GMs*self.y[n][i]*self.dt/self.r[n][i]**5)
                self.x[n].append(self.x[n][i]+self.vx[n][i+1]*self.dt)
                self.y[n].append(self.y[n][i]+self.vy[n][i+1]*self.dt)
                self.t[n].append(self.t[n][i]+self.dt)
                self.r[n].append(math.sqrt(self.x[n][i+1]**2+self.y[n][i+1]**2))
            for j in range(len(self.r[n])-2):
                if (self.r[n][j+1]**2-self.r[n][j]**2>0 and self.r[n][j+1]**2-self.r[n][j+2]**2>0):
                    xp[n].append(self.x[n][j+1])
                    yp[n].append(self.y[n][j+1])
                    tp[n].append(self.t[n][j+1])
                    if self.x[n][j+1]>=0 and self.y[n][j+1]/self.x[n][j+1]>=0:
                        theta[n].append(math.atan(self.y[n][j+1]/self.x[n][j+1])*180/math.pi)
                    if self.x[n][j+1]>=0 and self.y[n][j+1]/self.x[n][j+1]<0:
                        theta[n].append(math.atan(self.y[n][j+1]/self.x[n][j+1])*180/math.pi+360)
                    if self.x[n][j+1]<0 and self.y[n][j+1]/self.x[n][j+1]>=0:
                        theta[n].append(math.atan(self.y[n][j+1]/self.x[n][j+1])*180/math.pi+180)
                    if self.x[n][j+1]<0 and self.y[n][j+1]/self.x[n][j+1]<0:
                        theta[n].append(math.atan(self.y[n][j+1]/self.x[n][j+1])*180/math.pi+180)
            for k in range(len(theta[n])):
                xy[n].append(tp[n][k]*theta[n][k])
                x2[n].append(tp[n][k]**2)
            x_mean.append(float(sum(tp[n]))/len(tp[n]))
            y_mean.append(float(sum(theta[n]))/len(theta[n]))
            xy_mean.append(float(sum(xy[n]))/len(xy[n]))
            x2_mean.append(float(sum(x2[n]))/len(x2[n]))
            self.a.append(float((xy_mean[n]-x_mean[n]*y_mean[n]))/float((x2_mean[n]-x_mean[n]**2)))
            self.b.append(float((x2_mean[n]*y_mean[n]-x_mean[n]*xy_mean[n]))/float((x2_mean[n]-x_mean[n]**2)))
    def fit(self):
        for k in range(len(alfa)):
            xy1.append(alfa[k]*self.a[k])
            x21.append(alfa[k]**2)
        x_mean1=float(sum(alfa))/len(alfa)
        y_mean1=float(sum(self.a))/len(self.a)
        xy_mean1=float(sum(xy1))/len(xy1)
        x2_mean1=float(sum(x21))/len(x21)
        a=float((xy_mean1-x_mean1*y_mean1))/float((x2_mean1-x_mean1**2))
        b=float((x2_mean1*y_mean1-x_mean1*xy_mean1))/float((x2_mean1-x_mean1**2))
        print a,b
        for m in range(len(xf)):
            yf.append(a*xf[m]+b)
    def show_results(self):
        plt.plot(xf,yf,'g',label='least-squares line')
        plt.scatter(alfa,self.a,label='scatter')
        plt.title(u'Simulation of the precession of Mercury',fontsize=14)
        plt.xlabel(u'alpha',fontsize=14)
        plt.ylabel(u'$d\Theta/dt$(degrees/yr)',fontsize=14)
        plt.xlim(0,0.005)
        plt.ylim(0,60)
        plt.legend(fontsize=14,loc='best')
a=elliptical()
a.calculate()
a.fit()
a.show_results()
plt.show()

四、结论
当$V\, y=2\pi$，$\beta$改变时

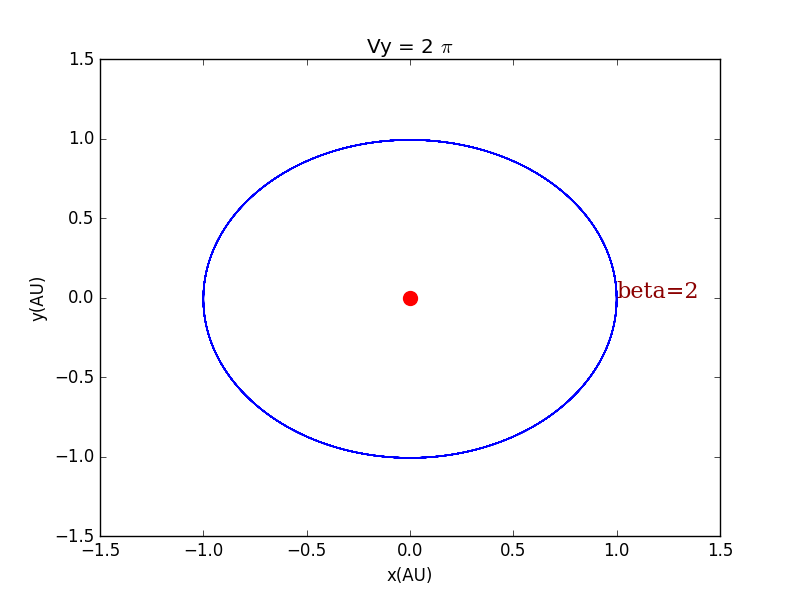
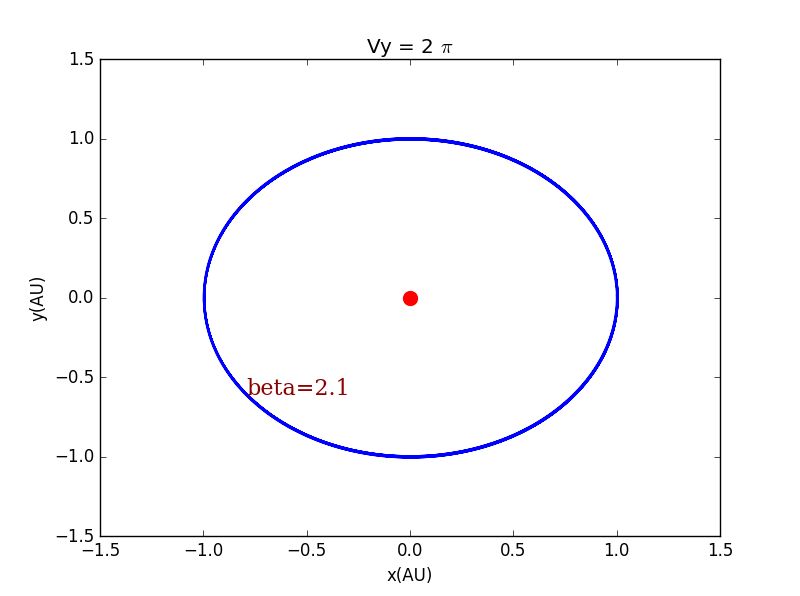
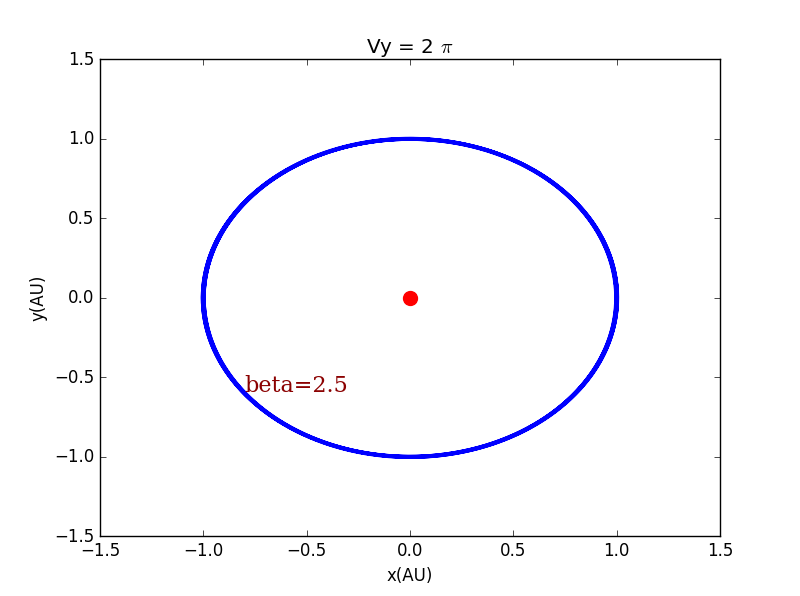
当$V\, y=2\pi$，$\beta$改变时时，行星轨道基本无变化。
三、致谢
感谢杜威同学对我本次作业的帮助！