第十次作业

作业

---

1、Abstract

In this exercise, the motion of Hyperion will be discussed according to the instruction of Problem4.21.Hyperion, also known as Saturn VII,is distinguished by its irregular shape,  chaotic rotation, and unexplained dumbball-like appearance.My work on Hyperion is just qualitative, aiming to show its chaotic during its orbit to Saturn.

2、Bankground

As we have known,Hyperion has an unusual shape,leading to its different behavior.Hyperion is shaped more like an egg and its orbit is choatic. We let$\theta$be the angle that the rod makes with the x axis and define the associated angular velocity$\omega =\frac{\mathrm{d} \theta }{\mathrm{d} t}$.The center of the mass of the object is$x_{c}$and$y_{c}$.
After some algebra,we can obtain:

$$\frac{\mathrm{d} \omega }{\mathrm{d} t}\approx -\frac{3GM_{Sat}}{r_{c}^{5}}\left ( x_{c}sin\theta -y_{c}cos\theta \right )\left ( x_{c}cos\theta +y_{c}sin\theta \right )$$
We can obtain$\omega$by using $\omega =\frac{\mathrm{d} \theta }{\mathrm{d} t}$

3.The Msin body

1.

import matplotlib.pyplot as plt
import numpy as np
import math
class hyperion:
    def __init__(self,GM=4*math.pi**2,dt=0.0001,time=10):
        self.GM=GM
        self.x=[1]
        self.y=[0]
        self.vx=[0]
        self.vy=[2*math.pi]
        self.dt=dt
        self.time=time
        self.r=[math.sqrt(self.x[0]**2+self.y[0]**2)]
        self.t=[0]
        self.w=[0]
        self.theta=[0]
    def calculate(self):
        for i in range(int(self.time//self.dt)):
            self.vx.append(self.vx[i]-self.GM*self.x[i]*self.dt/self.r[i]**3)
            self.vy.append(self.vy[i]-self.GM*self.y[i]*self.dt/self.r[i]**3)
            self.x.append(self.x[i]+self.vx[i+1]*self.dt)
            self.y.append(self.y[i]+self.vy[i+1]*self.dt)
            self.r.append(math.sqrt(self.x[i+1]**2+self.y[i+1]**2))
            self.w.append(self.w[i]-3*self.GM/self.r[i]**5*(self.x[i]*math.sin(self.theta[i])-self.y[i]*math.cos(self.theta[i]))*(self.x[i]*math.cos(self.theta[i])+self.y[i]*math.sin(self.theta[i]))*self.dt)
            self.theta.append(self.theta[i]+self.w[i+1]*self.dt)
            self.t.append(self.t[i]+self.dt)
            if self.theta[i+1]<-math.pi:
                self.theta[i+1]=self.theta[i+1]+2*math.pi
            if self.theta[i+1]>math.pi:
                self.theta[i+1]=self.theta[i+1]-2*math.pi
    def show_results(self,color):
        ax1=plt.subplot(121)
        ax2=plt.subplot(122)
        plt.sca(ax1)
        plt.plot(self.t,self.theta,'g',label=r'Circular orbit')
        plt.title(r'Hyperion  $\Theta$ versus time',fontsize=14)
        plt.xlabel(u'time(yr)',fontsize=14)
        plt.ylabel(u'$\Theta$(radians)',fontsize=14)
        plt.sca(ax2)
        plt.plot(self.t,self.w,'g',label=r'Circular orbit')
        plt.title(r'Hyperion  $\omega$ versus time',fontsize=14)
        plt.xlabel(u'time(yr)',fontsize=14)
        plt.ylabel(u'$\omega$(radians/yr)',fontsize=14)
        #plt.xlim(-1,1)
        #plt.ylim(-1,1)
        plt.legend(fontsize=14,loc='best')
a=hyperion()
a.calculate()
a.show_results('g')
plt.show()

2.

import matplotlib.pyplot as plt
import numpy as np
import math
class hyperion:
    def __init__(self,GM=4*math.pi**2,dt=0.0001,time=10):
        self.GM=GM
        self.x=[1]
        self.y=[0]
        self.vx=[0]
        self.vy=[5]
        self.dt=dt
        self.time=time
        self.r=[math.sqrt(self.x[0]**2+self.y[0]**2)]
        self.t=[0]
        self.w=[0]
        self.theta=[0]
    def calculate(self):
        for i in range(int(self.time//self.dt)):
            self.vx.append(self.vx[i]-self.GM*self.x[i]*self.dt/self.r[i]**3)
            self.vy.append(self.vy[i]-self.GM*self.y[i]*self.dt/self.r[i]**3)
            self.x.append(self.x[i]+self.vx[i+1]*self.dt)
            self.y.append(self.y[i]+self.vy[i+1]*self.dt)
            self.r.append(math.sqrt(self.x[i+1]**2+self.y[i+1]**2))
            self.w.append(self.w[i]-3*self.GM/self.r[i]**5*(self.x[i]*math.sin(self.theta[i])-self.y[i]*math.cos(self.theta[i]))*(self.x[i]*math.cos(self.theta[i])+self.y[i]*math.sin(self.theta[i]))*self.dt)
            self.theta.append(self.theta[i]+self.w[i+1]*self.dt)
            self.t.append(self.t[i]+self.dt)
            if self.theta[i+1]<-math.pi:
                self.theta[i+1]=self.theta[i+1]+2*math.pi
            if self.theta[i+1]>math.pi:
                self.theta[i+1]=self.theta[i+1]-2*math.pi
    def show_results(self,color):
        ax1=plt.subplot(121)
        ax2=plt.subplot(122)
        plt.sca(ax1)
        plt.plot(self.t,self.theta,'m',label=r'Elliptical orbit')
        plt.title(r'Hyperion  $\Theta$ versus time',fontsize=14)
        plt.xlabel(u'time(yr)',fontsize=14)
        plt.ylabel(u'$\Theta$(radians)',fontsize=14)
        plt.sca(ax2)
        plt.plot(self.t,self.w,'m',label=r'Elliptical orbit')
        plt.title(r'Hyperion  $\omega$ versus time',fontsize=14)
        plt.xlabel(u'time(yr)',fontsize=14)
        plt.ylabel(u'$\omega$(radians/yr)',fontsize=14)
        #plt.xlim(-1,1)
        #plt.ylim(-1,1)
        plt.legend(fontsize=14,loc='best')
a=hyperion()
a.calculate()
a.show_results('m')
plt.show()

3.

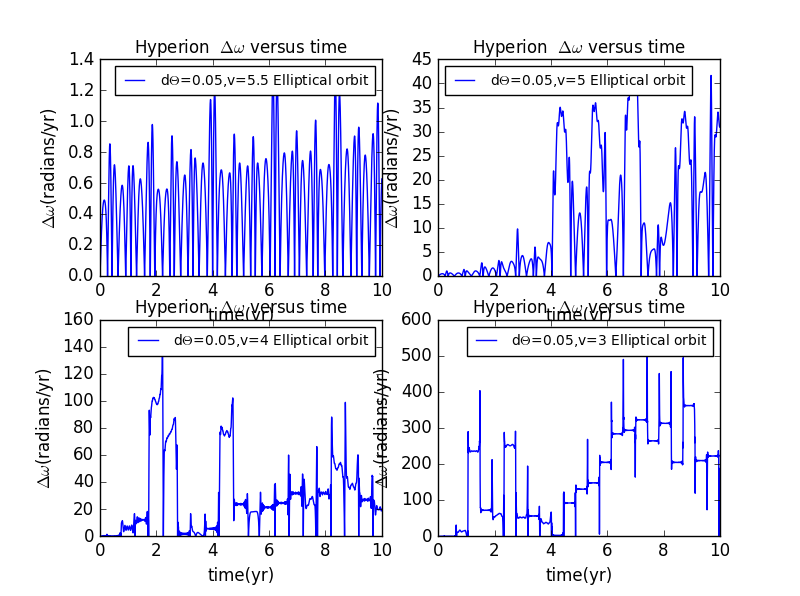
import matplotlib.pyplot as plt
import numpy as np
import math
class hyperion:
    def __init__(self,GM=4*math.pi**2,dt=0.0001,time=10):
        self.GM=GM
        self.x=[[1],[1],[1],[1]]
        self.y=[[0],[0],[0],[0]]
        self.vx=[[0],[0],[0],[0]]
        self.vy=[[5.5],[5],[4],[3]]
        self.x1=[[1],[1],[1],[1]]
        self.y1=[[0],[0],[0],[0]]
        self.vx1=[[0],[0],[0],[0]]
        self.vy1=[[5.5],[5],[4],[3]]
        self.dt=dt
        self.time=time
        self.r=[[math.sqrt(self.x[0][0]**2+self.y[0][0]**2)],[math.sqrt(self.x[1][0]**2+self.y[1][0]**2)],[math.sqrt(self.x[2][0]**2+self.y[2][0]**2)],[math.sqrt(self.x[3][0]**2+self.y[3][0]**2)]]
        self.t=[[0],[0],[0],[0]]
        self.w=[[0],[0],[0],[0]]
        self.theta=[[0.05],[0.05],[0.05],[0.05]]
        self.r1=[[math.sqrt(self.x1[0][0]**2+self.y1[0][0]**2)],[math.sqrt(self.x1[1][0]**2+self.y1[1][0]**2)],[math.sqrt(self.x1[2][0]**2+self.y1[2][0]**2)],[math.sqrt(self.x1[3][0]**2+self.y1[3][0]**2)]]
        self.t1=[[0],[0],[0],[0]]
        self.w1=[[0],[0],[0],[0]]
        self.theta1=[[0],[0],[0],[0]]
        self.d=[[math.log(abs(self.theta[0][0]-self.theta1[0][0]))],[math.log(abs(self.theta[1][0]-self.theta1[1][0]))],[math.log(abs(self.theta[2][0]-self.theta1[2][0]))],[math.log(abs(self.theta[3][0]-self.theta1[3][0]))]]
        self.dw=[[abs(self.w[0][0]-self.w1[0][0])],[abs(self.w[1][0]-self.w1[1][0])],[abs(self.w[2][0]-self.w1[2][0])],[abs(self.w[3][0]-self.w1[3][0])]]
    def calculate(self):
        for n in range(4):
            for i in range(int(self.time//self.dt)):
                self.vx[n].append(self.vx[n][i]-self.GM*self.x[n][i]*self.dt/self.r[n][i]**3)
                self.vy[n].append(self.vy[n][i]-self.GM*self.y[n][i]*self.dt/self.r[n][i]**3)
                self.x[n].append(self.x[n][i]+self.vx[n][i+1]*self.dt)
                self.y[n].append(self.y[n][i]+self.vy[n][i+1]*self.dt)
                self.r[n].append(math.sqrt(self.x[n][i+1]**2+self.y[n][i+1]**2))
                self.w[n].append(self.w[n][i]-3*self.GM/self.r[n][i]**5*(self.x[n][i]*math.sin(self.theta[n][i])-self.y[n][i]*math.cos(self.theta[n][i]))*(self.x[n][i]*math.cos(self.theta[n][i])+self.y[n][i]*math.sin(self.theta[n][i]))*self.dt)
                self.theta[n].append(self.theta[n][i]+self.w[n][i+1]*self.dt)
                self.t[n].append(self.t[n][i]+self.dt)
                if self.theta[n][i+1]<-math.pi:
                    self.theta[n][i+1]=self.theta[n][i+1]+2*math.pi
                if self.theta[n][i+1]>math.pi:
                    self.theta[n][i+1]=self.theta[n][i+1]-2*math.pi
                self.vx1[n].append(self.vx1[n][i]-self.GM*self.x1[n][i]*self.dt/self.r1[n][i]**3)
                self.vy1[n].append(self.vy1[n][i]-self.GM*self.y1[n][i]*self.dt/self.r1[n][i]**3)
                self.x1[n].append(self.x1[n][i]+self.vx1[n][i+1]*self.dt)
                self.y1[n].append(self.y1[n][i]+self.vy1[n][i+1]*self.dt)
                self.r1[n].append(math.sqrt(self.x1[n][i+1]**2+self.y1[n][i+1]**2))
                self.w1[n].append(self.w1[n][i]-3*self.GM/self.r1[n][i]**5*(self.x1[n][i]*math.sin(self.theta1[n][i])-self.y1[n][i]*math.cos(self.theta1[n][i]))*(self.x1[n][i]*math.cos(self.theta1[n][i])+self.y1[n][i]*math.sin(self.theta1[n][i]))*self.dt)
                self.theta1[n].append(self.theta1[n][i]+self.w1[n][i+1]*self.dt)
                self.t1[n].append(self.t1[n][i]+self.dt)
                if self.theta1[n][i+1]<-math.pi:
                    self.theta1[n][i+1]=self.theta1[n][i+1]+2*math.pi
                if self.theta1[n][i+1]>math.pi:
                    self.theta1[n][i+1]=self.theta1[n][i+1]-2*math.pi
                self.d[n].append(math.log(abs(self.theta[n][i]-self.theta1[n][i])))
                self.dw[n].append(abs(self.w[n][i]-self.w1[n][i]))
    def show_results(self,color):
        ax1=plt.subplot(221)
        ax2=plt.subplot(222)
        ax3=plt.subplot(223)
        ax4=plt.subplot(224)
        plt.sca(ax1)
plt.plot(self.t[0],self.d[0],'g',label=r'd$\Theta$=0.05,v=5.5 Elliptical orbit')
        #plt.plot(self.t[0],self.dw[0],'b',label=r'd$\Theta$=0.05,v=5.5 Elliptical orbit')
        plt.title(r'Hyperion  $\Delta{\Theta}$ versus time',fontsize=12)
        #plt.title(r'Hyperion  $\Delta{\omega}$ versus time',fontsize=12)
        plt.xlabel(u'time(yr)',fontsize=12)
        plt.ylabel(u'$\Delta{\Theta}$(radians)',fontsize=12)
        #plt.ylabel(u'$\Delta{\omega}$(radians/yr)',fontsize=12)
        plt.legend(fontsize=10,loc='best')
        plt.sca(ax2)
        plt.plot(self.t[1],self.d[1],'g',label=r'd$\Theta$=0.05,v=5 Elliptical orbit')
        #plt.plot(self.t[1],self.dw[1],'b',label=r'd$\Theta$=0.05,v=5 Elliptical orbit')
        plt.title(r'Hyperion  $\Delta{\Theta}$ versus time',fontsize=12)
        #plt.title(r'Hyperion  $\Delta{\omega}$ versus time',fontsize=12)
        plt.xlabel(u'time(yr)',fontsize=12)
        plt.ylabel(u'$\Delta{\Theta}$(radians)',fontsize=12)
        #plt.ylabel(u'$\Delta{\omega}$(radians/yr)',fontsize=12)
        plt.legend(fontsize=10,loc='best')
        plt.sca(ax3)
        plt.plot(self.t[2],self.d[2],'g',label=r'd$\Theta$=0.05,v=4 Elliptical orbit')
        #plt.plot(self.t[2],self.dw[2],'b',label=r'd$\Theta$=0.05,v=4 Elliptical orbit')
        plt.title(r'Hyperion  $\Delta{\Theta}$ versus time',fontsize=12)
        #plt.title(r'Hyperion  $\Delta{\omega}$ versus time',fontsize=12)
        plt.xlabel(u'time(yr)',fontsize=12)
        plt.ylabel(u'$\Delta{\Theta}$(radians)',fontsize=12)
        #plt.ylabel(u'$\Delta{\omega}$(radians/yr)',fontsize=12)
        plt.legend(fontsize=10,loc='best')
        plt.sca(ax4)
        plt.plot(self.t[3],self.d[3],'g',label=r'd$\Theta$=0.05,v=3 Elliptical orbit')
        #plt.plot(self.t[3],self.dw[3],'b',label=r'd$\Theta$=0.05,v=3 Elliptical orbit')
        plt.title(r'Hyperion  $\Delta{\Theta}$ versus time',fontsize=12)
        #plt.title(r'Hyperion  $\Delta{\omega}$ versus time',fontsize=12)
        plt.xlabel(u'time(yr)',fontsize=12)
        plt.ylabel(u'$\Delta{\Theta}$(radians)',fontsize=12)
        #plt.ylabel(u'$\Delta{\omega}$(radians/yr)',fontsize=12)
        plt.legend(fontsize=10,loc='best')
a=hyperion()
a.calculate()
a.show_results('b')
plt.show()

4. Conclusion

for circular and elliptical orbit,reset$\theta$


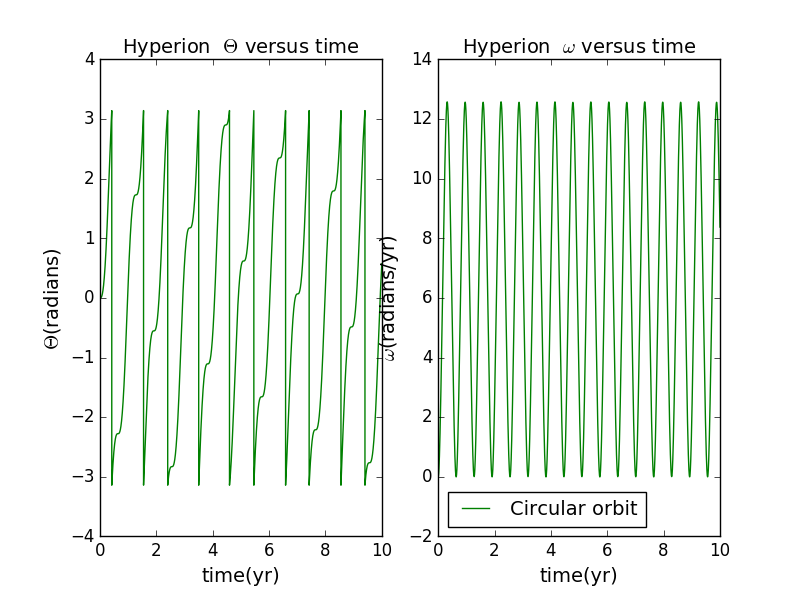
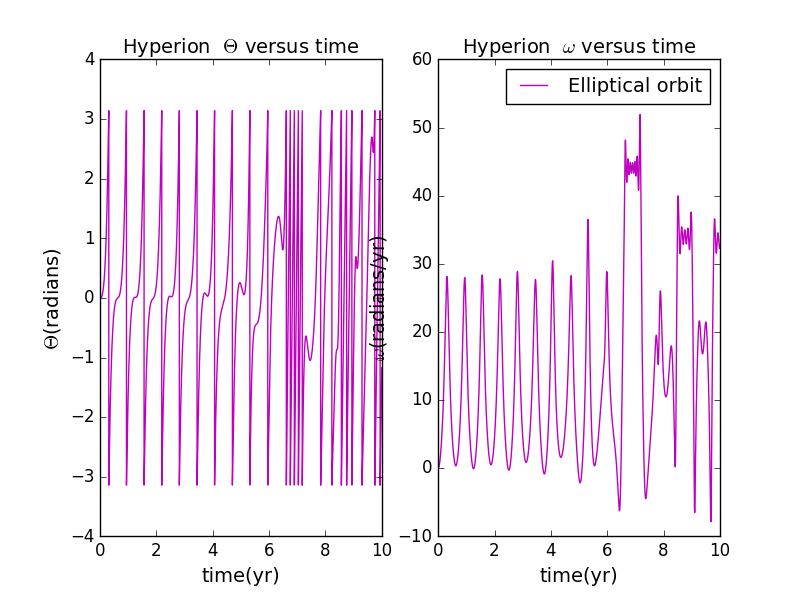
$\Delta \theta$ and $\Delta \omega$for circular and elliptical orbit reset $\theta$


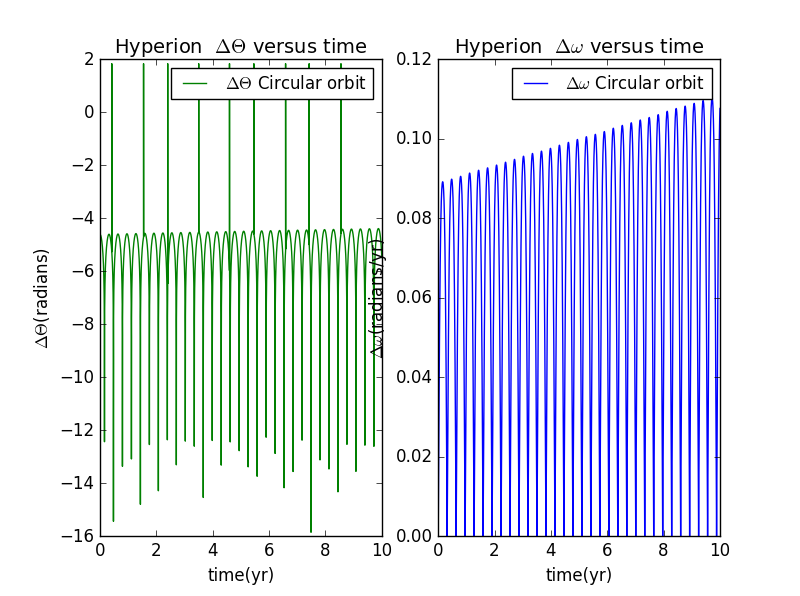
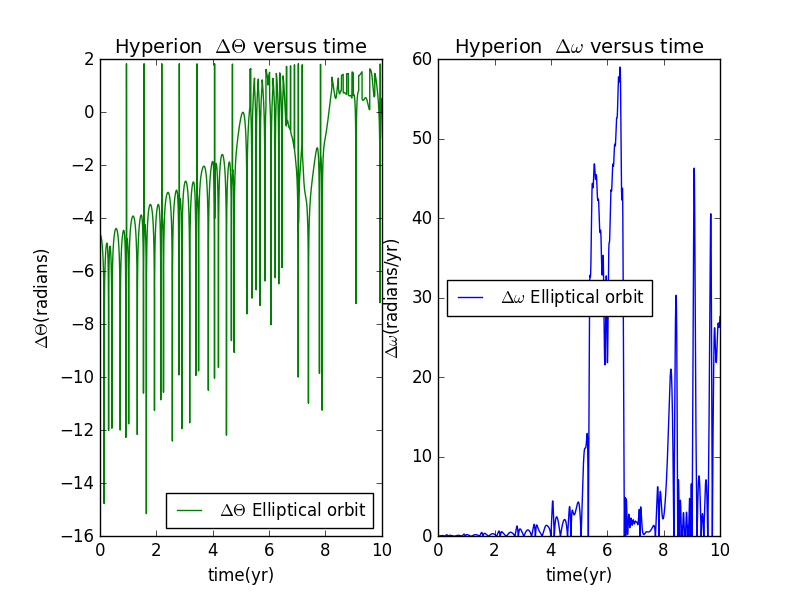
not keep$\theta$in range from$-\pi$to$\pi$for circular and elliptical orbit


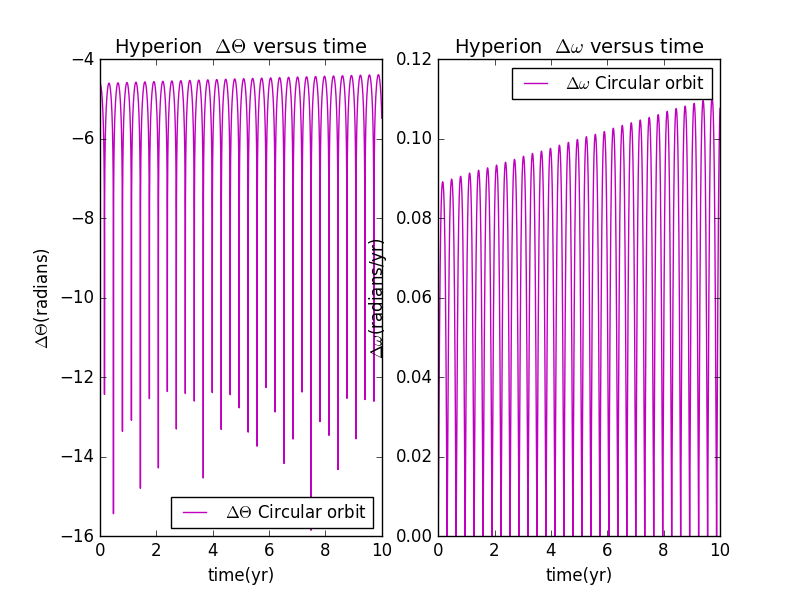
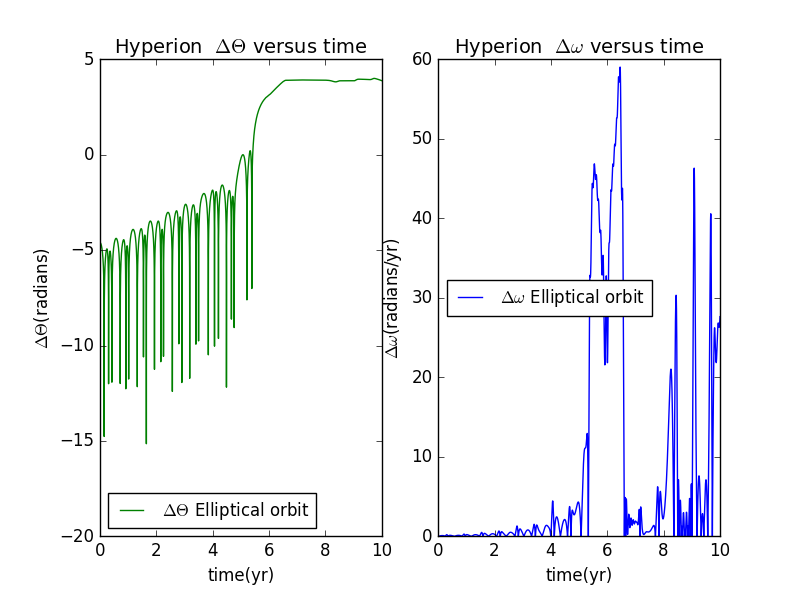
change the initial conditions
$\Delta \theta=0.01$,change the initial velocity


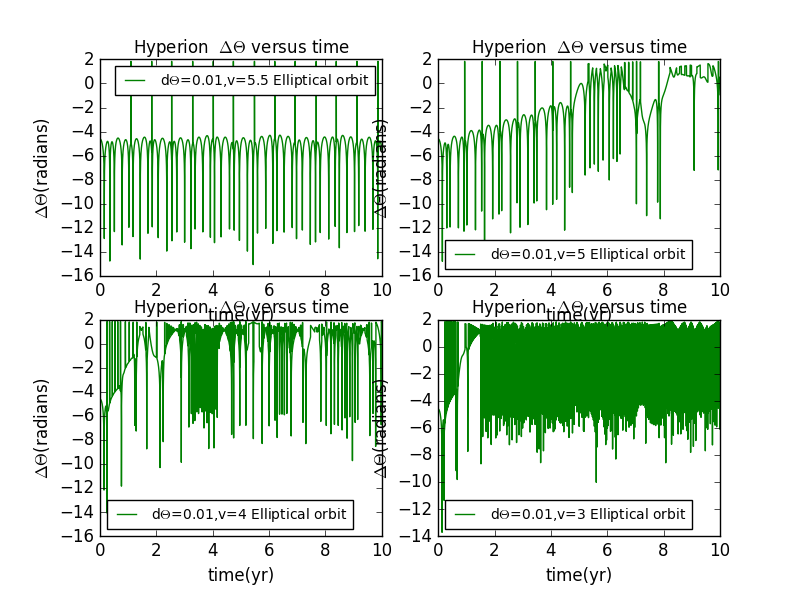
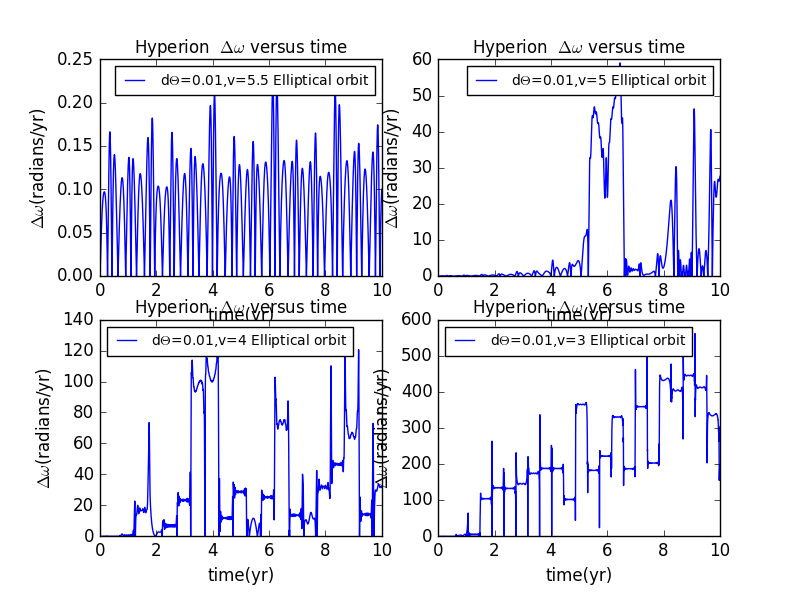
$\Delta \theta=0.05$,change the initial velocity

5 Thanks

感谢杜威同学的帮助！