期末作业

作业

第七章 随机系统

摘要

本文主要用Python语言对部分随机过程做了模拟，通过观察数值计算的结果，并将其与概率论的结论相比较，证明数值计算的结果在处理随机过程方面是可信的。

布尔运动 ； 随机行走

背景

　　随机系统在生活中占据重要的位置，小到平时打牌打麻将，大到金融股票市场，都有随机的现。处理随机系统时，我们可以举出所有影响因素，但是这会带来天文数字的微分方程，难以实际求解。为此，我们往往使用概率论来描述随机系统。
　　
　　
　　在许多随机过程中，这里我讨论的是随机行走问题。
　　一维情况下的随机行走问题，指的是一个粒子初始时刻位于原点，之后每次经过同样的时间间隔，其或者向左行走或者向右行走，两个方向的概率可能相同，也可能不同，步长可能一定也可能在一个范围内随机。其二维情况下则其每一步的方向任意，其它性质和一维情况相似。

正文

一。左右等可能随机行走（步长一定）

这里我们考虑一个典型的一维随机行走问题。粒子初始时刻位于x=0处，步长为1，相邻的两步之间时间间隔固定（故步数正比于时间），每一步向左和向右概率均为0.5。我们假设有5000个相同的粒子，观察它们运动的平均性质。
它们距离原点的平均距离随步数的变化关系:
1 程序

from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
steps = np.linspace(0, 100, 101)
x_ave = np.zeros(101)
x_y0 = np.zeros(101)
x_now = np.zeros(5000)
for i in range(100):
    for j in range(5000):
        ruler = np.random.rand()
        if ruler<=0.5:
            x_now[j] = x_now[j] + 1
        else:
            x_now[j] = x_now[j] - 1
    average = sum(x_now)/5000
    x_ave[i+1] = average
plt.scatter(steps, x_ave)
plt.plot(steps, x_y0)
plt.xlim(0,100)
plt.ylim(-1,1)
plt.grid(True)
plt.xlabel('step number(= time)')
plt.ylabel('<x>')
plt.title('<x> of 5000 walkers')
plt.show()

2图像

可见，这个系统中粒子距离原点的平均距离保持在0附近波动。按照概率论，粒子向左向右的概率相同，其距离原点的平均距离应该为0。这里数值结果和理论结果是一致的。
它们距离原点距离平方随步数的变化关系:
1 程序

from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
steps = np.linspace(0, 100, 101)
x2_ave = np.zeros(101)
x_y0 = np.zeros(101)
x_now = np.zeros(5000)
x2_now = np.zeros(5000)
for i in range(100):
    for j in range(5000):
        ruler = np.random.rand()
        if ruler<=0.5:
            x_now[j] = x_now[j] + 1
        else:
            x_now[j] = x_now[j] - 1
        x2_now[j] = x_now[j]**2
    average2 = sum(x2_now)/5000
    x2_ave[i+1] = average2
para = np.polyfit(steps, x2_ave,1)
poly = np.poly1d(para)
y_fit = poly(steps)
plt.scatter(steps, x2_ave,s=2)
plt.plot(steps, y_fit, 'r', label = 'fit line')
plt.legend(loc='upper left')
plt.xlim(0,100)
plt.ylim(0,100)
plt.grid(True)
plt.xlabel('step number(= time)')
plt.ylabel('<x^2>')
plt.title('<x^2> of 5000 walkers')
plt.show()

2 图像

x的平方的平均值与步数近似为线性关系。这种线性关系在一维扩散系统中也有出现，表明这个随机行走的过程是“类扩散的”。

二。左右等可能随机行走（步长不一定）

下来我们将情况一般化，此时每一步的步长为-1~+1之间的一个值，且取每一个值的概率是一定的。此时两个平均值随步数的变化关系：

from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
steps = np.linspace(0, 100, 101)
x_ave = np.zeros(101)
x_y0 = np.zeros(101)
x_now = np.zeros(5000)
for i in range(100):
    for j in range(5000):
        length = 2*np.random.rand() - 1      
        x_now[j] = x_now[j] + length
    average = sum(x_now)/5000
    x_ave[i+1] = average
plt.scatter(steps, x_ave)
plt.plot(steps, x_y0)
plt.xlim(0,100)
plt.ylim(-1,1)
plt.grid(True)
plt.xlabel('step number(= time)')
plt.ylabel('<x>')
plt.title('<x> of 5000 walkers, random step length')
plt.show()

2 图像

可见，这个系统中粒子距离原点的平均距离保持在0附近波动。按照概率论，粒子向左向右的概率相同，其距离原点的平均距离应该为0。这里数值结果和理论结果是一致的。

它们距离原点距离平方随步数的变化关系:
1 程序

from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
steps = np.linspace(0, 100, 101)
x2_ave = np.zeros(101)
x_y0 = np.zeros(101)
x_now = np.zeros(5000)
x2_now = np.zeros(5000)
for i in range(100):
    for j in range(5000):
        length = 2*np.random.rand() - 1
        x_now[j] = x_now[j] + length
        x2_now[j] = x_now[j]**2
    average2 = sum(x2_now)/5000
    x2_ave[i+1] = average2
para = np.polyfit(steps, x2_ave,1)
poly = np.poly1d(para)
y_fit = poly(steps)
plt.scatter(steps, x2_ave,s=2)
plt.plot(steps, y_fit, 'r', label = 'fit line')
plt.legend(loc='upper left')
plt.xlim(0,100)
plt.ylim(0,100)
plt.grid(True)
plt.xlabel('step number(= time)')
plt.ylabel('<x^2>')
plt.title('<x^2> of 5000 walkers, random step length')
plt.show()

2 图像

由图可知，此时x的平均值在0附近波动，x的平方的平均值与步数近似为线性关系，此过程也是“类扩散的”。

三、左右不等可能的随机行走

这里我们考察当向左向右的运动概率不相同时的情况。我们让向右行走的概率为0.75，向左为0.25，固定步长为1，观察两种平均值随步长的变化关系为
1 程序

from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
steps = np.linspace(0, 100, 101)
x_ave = np.zeros(101)
x_now = np.zeros(5000)
for i in range(100):
    for j in range(5000):
        ruler = np.random.rand()
        if ruler<=0.75:
            x_now[j] = x_now[j] + 1
        else:
            x_now[j] = x_now[j] - 1
    average = sum(x_now)/5000
    x_ave[i+1] = average
para = np.polyfit(steps, x_ave,1)
poly = np.poly1d(para)
y_fit = poly(steps)
plt.scatter(steps, x_ave, s=5)
plt.plot(steps, y_fit, 'r', label = 'fit line')
plt.legend(loc='upper left')
plt.xlim(0,100)
plt.grid(True)
plt.xlabel('step number(= time)')
plt.ylabel('<x>')
plt.title('<x> of 5000 walkers')
plt.show()

2 图像

它们距离原点距离平方随步数的变化关系:
1 程序

from __future__ import division
import numpy as np
import matplotlib.pyplot as plt
steps = np.linspace(0, 100, 101)
x2_ave = np.zeros(101)
x_y0 = np.zeros(101)
x_now = np.zeros(5000)
x2_now = np.zeros(5000)
for i in range(100):
    for j in range(5000):
        ruler = np.random.rand()
        if ruler<=0.75:
            x_now[j] = x_now[j] + 1
        else:
            x_now[j] = x_now[j] - 1
        x2_now[j] = x_now[j]**2
    average2 = sum(x2_now)/5000
    x2_ave[i+1] = average2
para = np.polyfit(steps, x2_ave,2)
poly = np.poly1d(para)
y_fit = poly(steps)
plt.scatter(steps, x2_ave,s=2)
plt.plot(steps, y_fit, 'r', label = 'fit line (order 2)')
plt.legend(loc='upper left')
plt.xlim(0,100)
plt.grid(True)
plt.xlabel('step number(= time)')
plt.ylabel('<x^2>')
plt.title('<x^2> of 5000 walkers')
plt.show()

2 图像

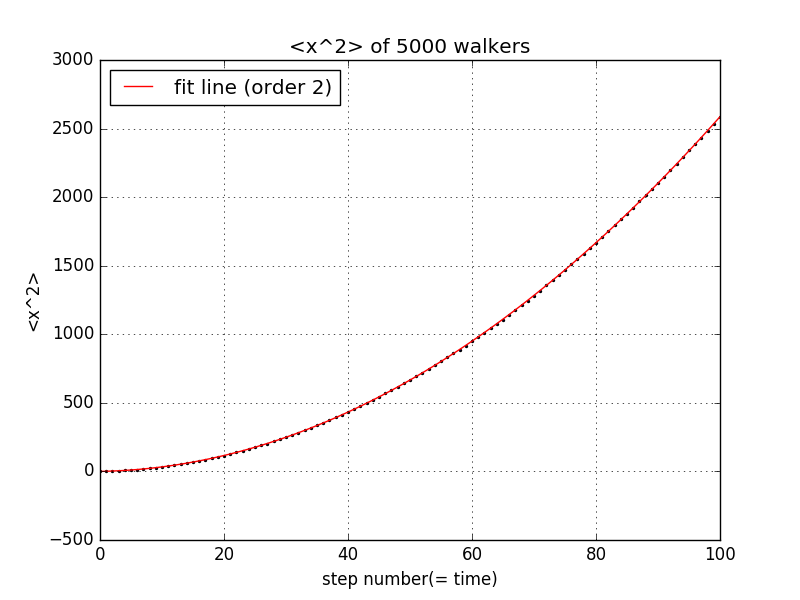
由图可知，x的平均值随步数线性增大，其平方的平均与步数成二次关系。这与概率论的结论相同。

结论

1.对于一维的等可能随机行走，左右步长一定时，其与原点的距离平均值在0附近，距离平方的平均值线性增加。
2.对于左右步长随机（-1~+1等可能）的随机行走，结论不变，只是距离平方的平均值的增加速度降低。
3.对于左右不等可能的随机行走，在左右步长一定时，距离平均值线性增肌，距离平方的平均值二次型增加。
4.python模拟结论和概率论的结果一致！

参考资料

《计算物理》第七章。